最短路径--------Floyd算法剖析
QQ ：375061590
到两个重要矩阵：
1.d[numVex][numVex] (numVex图的顶点数)：最开始该矩阵就是图的邻接矩阵，经过Floyd算法处理开后，d[numVex][numVex]中的d[i][j]，表示着从顶点i到j的最短路径的权重。
2.p[numVex][numVex]：p[i][j]表示从i到j的最短路径上 i的后继，例如1到5最短路劲为1-2-4-5 那么p[1][5]==2 ，最开始构建的p矩阵中p[i][j]= j
算法核心思想： 三圈for循环
1 for (int k = 0; k < graph.getNumVex(); k++) { 2 3 for (int v = 0; v < graph.getNumVex(); v++) { 4 5 for (int w = 0; w < graph.getNumVex(); w++) { 6 7 if (d[v][w] > d[v][k] + d[k][w]) { 8 9 d[v][w] = d[v][k] + d[k][w]; 10 11 p[v][w] = p[v][k];// p[v][w]是v--w最短路径上 v的下一顶点 12 13 } 14 15 } 16 17 } 18 19 } 20 21
第一层 k是作为中间顶点
第二层 v是作为起始顶点
第三层 w是作为终点顶点
内层核心代码：
以v为起点，w为终点，再以k作为v和w之间的中间点，去判断d[v][ w]和d[v][k] + d[k][w]的大小关系，如果d[v][w] > d[v][k] + d[k][w]，说明找到从v→w的更短路径了，此时更改d[v][w]的值为d[v][k] + d[k][w]。
p[v][w]的值也要相应改成p[v][k]的值，因为 p[v][k]的值是v→k最短路径上v的后继顶点，而v→w这段最短路径是连接在v→k这段路径后面的，所以令所当然p[v][w]也要指向p[v][k]。
注意：最外层的k循环，前面的n此循环的结果跟后面n+1次循环的错做过程是息息相关，
三次循环完成后，各个顶点之间的最短路径权重会存储在d矩阵中：d[i][j]表示i→j的最短路径权重。
p中则存储着路径上的顶点，如果把i→j最短路径上的顶点列出来呢？
代码：
1 2 3 //求start→end 最短路径上的顶点 4 5 StringBuilder path = new StringBuilder(); 6 7 int index = start;//起始点 8 9 path.append(start + " → "); 10 11 while (index != end) { 12 13 //循环取出路径上的各个顶点 14 15 index = p[index][end]; 16 17 if(index != end){ 18 19 path.append(index + " →"); 20 21 }
用一个while循环循环 index = p[index][end];直到达到终点
假设该最短路径为 start→A→B→C→end
则执行过程是：
index = p[start][end]; →A path== start→A → index = p[A][end]; →B path== start→A →B → index = p[B][end]; →C path== start→A →B →C→ index = p[C][end]; →end path== start→A →B →C→end
测试：
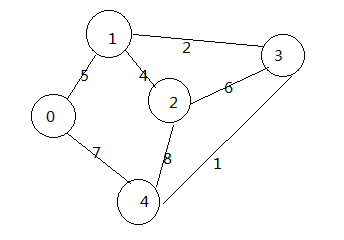
请输入定点的数目:5 顶点数为：5 请输入边数:7 边数为：7 请输入（Vi，Vj）上下标i 和 j，以及权重，用逗号隔开 0,1,5 0,4,7 1,2,4 4,2,8 1,3,2 2,3,6 4,3,1 初始的d矩阵 0 5 9999 9999 7 5 0 4 2 9999 9999 4 0 6 8 9999 2 6 0 1 7 9999 8 1 0 初始的p矩阵 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 处理后的d矩阵 0 5 9 7 7 5 0 4 2 3 9 4 0 6 7 7 2 6 0 1 7 3 7 1 0 处理后的p矩阵 0 1 1 1 4 0 1 2 3 3 1 1 2 3 3 1 1 2 3 4 0 3 3 3 4 求最短路径 请输入起点： 0 请输入终点： 2 从0到2的最短路径为9 该路劲为：0 → 1 →2 是否继续计算其他最短路径 Y/N? y 求最短路径 请输入起点： 0 请输入终点： 3 从0到3的最短路径为7 该路劲为：0 → 1 →3 是否继续计算其他最短路径 Y/N? y 求最短路径 请输入起点： 4 请输入终点： 1 从4到1的最短路径为3 该路劲为：4 → 3 →1 是否继续计算其他最短路径 Y/N? y 求最短路径 请输入起点： 2 请输入终点： 4 从2到4的最短路径为7 该路劲为：2 → 3 →4 是否继续计算其他最短路径 Y/N?
package DataStructure; import java.util.Scanner; public class Floyd { private Graph graph; private int[][] d;// 用来存储顶点到顶点之间最短路径的权重 private int[][] p;// p[1][5]表示1到5的最短路径上 1的后继，例如1到5最短路劲为1-2-4-5 那么p[1][5]==2 public Floyd() { this.graph = new Graph(); d = graph.getArc(); p = new int[graph.getNumVex()][graph.getNumVex()]; initP();// 初始化矩阵p System.out.println("初始的d矩阵\n"); for (int i = 0; i < graph.getNumVex(); i++) { for (int j = 0; j < graph.getNumVex(); j++) { System.out.print(d[i][j] + " "); } System.out.println("\n"); } System.out.println("初始的p矩阵\n"); for (int i = 0; i < graph.getNumVex(); i++) { for (int j = 0; j < graph.getNumVex(); j++) { System.out.print(p[i][j] + " "); } System.out.println("\n"); } work(); System.out.println("处理后的d矩阵\n"); for (int i = 0; i < graph.getNumVex(); i++) { for (int j = 0; j < graph.getNumVex(); j++) { System.out.print(d[i][j] + " "); } System.out.println("\n"); } System.out.println("处理后的p矩阵\n"); for (int i = 0; i < graph.getNumVex(); i++) { for (int j = 0; j < graph.getNumVex(); j++) { System.out.print(p[i][j] + " "); } System.out.println("\n"); } } /** * 初始化p矩阵 * */ private void initP() { for (int i = 0; i < graph.getNumVex(); i++) { for (int j = 0; j < graph.getNumVex(); j++) { p[i][j] = j; } } } /** * 对d和p进行变化 * */ private void work() { for (int k = 0; k < graph.getNumVex(); k++) { for (int v = 0; v < graph.getNumVex(); v++) { for (int w = 0; w < graph.getNumVex(); w++) { if (d[v][w] > d[v][k] + d[k][w]) { d[v][w] = d[v][k] + d[k][w]; p[v][w] = p[v][k];// p[v][w]是v--w最短路径上 v的下一顶点 } } } } } /** * 获取最短路劲 * */ public void getShortestPath(int start, int end) { StringBuilder path = new StringBuilder(); int index = start;// 起始点 path.append(start + " → "); while (index != end) { // 循环取出路径上的各个顶点 index = p[index][end]; if (index != end) { path.append(index + " →"); }else { path.append(index); } } System.out.println("从" + (start) + "到" + (end) + "的最短路径为" + d[start][end] + "\n该路劲为：" + path.toString()); } public static void getShortestPath(Floyd floyd) { Scanner scanner = new Scanner(System.in); System.out.println("求最短路径\n请输入起点："); int start = scanner.nextInt(); System.out.println("请输入终点："); int end = scanner.nextInt(); floyd.getShortestPath(start, end); System.out.println("是否继续计算其他最短路径 Y/N? "); String tag = scanner.next(); if (tag.toLowerCase().equals("y")) { getShortestPath(floyd); } } /** * 图内部类 * * @author ccf * */ class Graph { /** * 定点数 * */ private int numVex = 0; private int arc[][] = null; private int numEdge = 0; private final int INFINITY = 9999; public Graph() { System.out.print("请输入定点的数目:"); Scanner scanner = new Scanner(System.in); this.numVex = scanner.nextInt(); arc = new int[numVex][numVex]; for (int i = 0; i < numVex; i++) { for (int j = 0; j < numVex; j++) { arc[i][j] = INFINITY; } } for (int i = 0; i < numVex; i++) { arc[i][i] = 0; } System.out.println("顶点数为：" + this.numVex); System.out.print("请输入边数:"); scanner = new Scanner(System.in); this.numEdge = scanner.nextInt(); System.out.println("边数为：" + this.numEdge); System.out.println("请输入（Vi，Vj）上下标i 和 j，以及权重，用逗号隔开"); for (int i = 1; i <= numEdge; i++) { scanner = new Scanner(System.in); String a = scanner.nextLine(); String[] b = a.split(","); // System.out // .println("输入了：" + Integer.parseInt(b[0]) + " " // + Integer.parseInt(b[1]) + " " // + Integer.parseInt(b[2])); arc[Integer.parseInt(b[0])][Integer.parseInt(b[1])] = Integer .parseInt(b[2]); arc[Integer.parseInt(b[1])][Integer.parseInt(b[0])] = Integer .parseInt(b[2]); } } public int[][] getArc() { return arc; } public int getNumVex() { return numVex; } } public static void main(String[] args) { Floyd floyd = new Floyd(); getShortestPath(floyd); } }
