树状数组

一：树状数组的基础知识点  我的另一个博客

二：树状数组的基础操作 具体代码以及题目

　　1.单点更新，区间查询

 

int lowbit(int x)
{
    return x&(-x);
}

int sum(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i)){
        ans+=a[i];
    }
    return ans;
}

void updata(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i)){
        a[i]+=y;
    }
}
void solve()
{
    updata(x,y);
    printf("%d\n",sum(y)-sum(x-1));1-1,y1-1));
}

 

 

 

　　2，区间更新，单点查询

　　　了解差分：

　　    通过“差分”（就是记录数组中每个元素与前一个元素的差，如果求第i的值是多少 那么就是把差分数组从1,2,3......i相加 就是第i个的值），所以可以把这个问         

 

int lowbit(int x)
{
    return x&(-x);
}
void updata(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i)){
        s[i]+=y;
    }
}
int sum(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i)){
        ans+=s[i];
    }
    return ans;
}
void solve()
{
    updata(a,1);
    updata(b+1,-1);
    printf("%d\n",sum(y));
}

　　3，区间更新，区间查询

　　

int lowbit(int x)
{
    return x&(-x);
}
void updata(int p,long long x)
{
    for(int i=p;i<=n;i+=lowbit(i)){
        s1[i]+=x;
        s2[i]+=x*p;
    }
}
long long sum(int p)
{
    long long ans=0;
    for(int i=p;i>0;i-=lowbit(i)){
        ans+=s1[i]*(p+1)-s2[i];
    }
    return ans;
}
void solve()
{
    updata(a,1);
    updata(b+1,-1);
    printf("%d\n",sum(y)-sum(x-1));
}

　　4：二维树状数组

          单点更新  区间查询

我们已　　经学会了对于序列的常用操作，那么我们不由得想到…… 能不能把类似的操作应用到矩阵上呢？这时候我们就要写二维树状数组了！

在一维　　树状数组中，tree[x]（树状数组中的那个“数组”）记录的是右端点为x、长度为lowbit(x)的区间的区间和。
那么在　　二维树状数组中，可以类似地定义tree[x][y]记录的是右下角为(x, y)，高为lowbit(x), 宽为 lowbit(y)的区间的区间和。

int lowbit(int x)
{
    return x&(-x);
}

void updata(int x,int y,int z)
{
    for(int i=x;i<=n;i+=lowbit(i)){
        for(int j=y;j<=m;j+=lowbit(j)){
            s[i][j]+=z;
        }
    }
}

long long sum(int x,int y)
{
    long long res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        for(int j=y;j>0;j-=lowbit(j)){
            res+=s[i][j];
        }
    }
    return res;
}

void solve()
{
    updata(x,y,z);
    //这个是求面积的公式 画图会比较好理解
    printf("%lld\n",sum(x2,y2)+sum(x1-1,y1-1)-sum(x1-1,y2)-sum(x2,y1-1));
}

      区间更新 单点查询

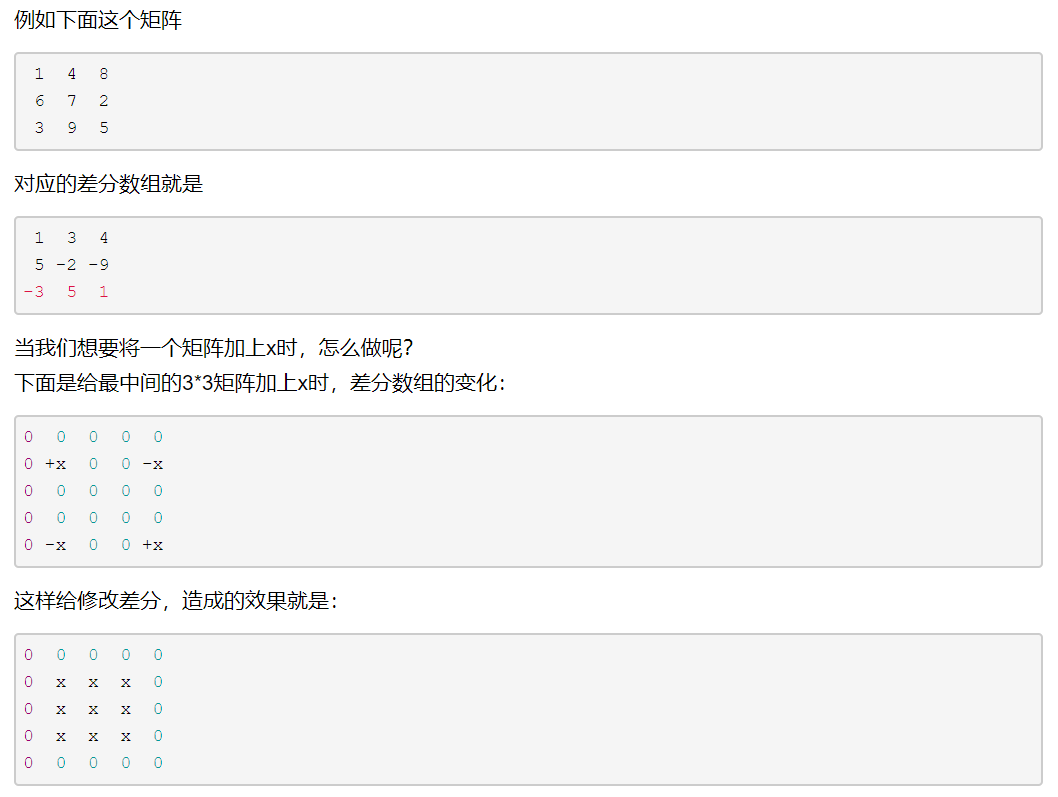
int lowbit(int x)
{
    return x&(-x);
}
void updata(int x,int y,int z)
{
    for(int i=x;i<=n;i+=lowbit(i)){
        for(int j=y;j<=n;j+=lowbit(j)){
            s[i][j]+=z;
        }
    }
}

int sum(int x,int y)
{
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        for(int j=y;j>0;j-=lowbit(j)){
            res+=s[i][j];
        }
    }
    return res;
}

void solve()
{
    updata(x1,y1,1);
    updata(x2+1,y1,-1);
    updata(x1,y2+1,-1);
    updata(x2+1,y2+1,1);
    printf("%d\n",sum(x,y));
}

 

区间更新 区间查询

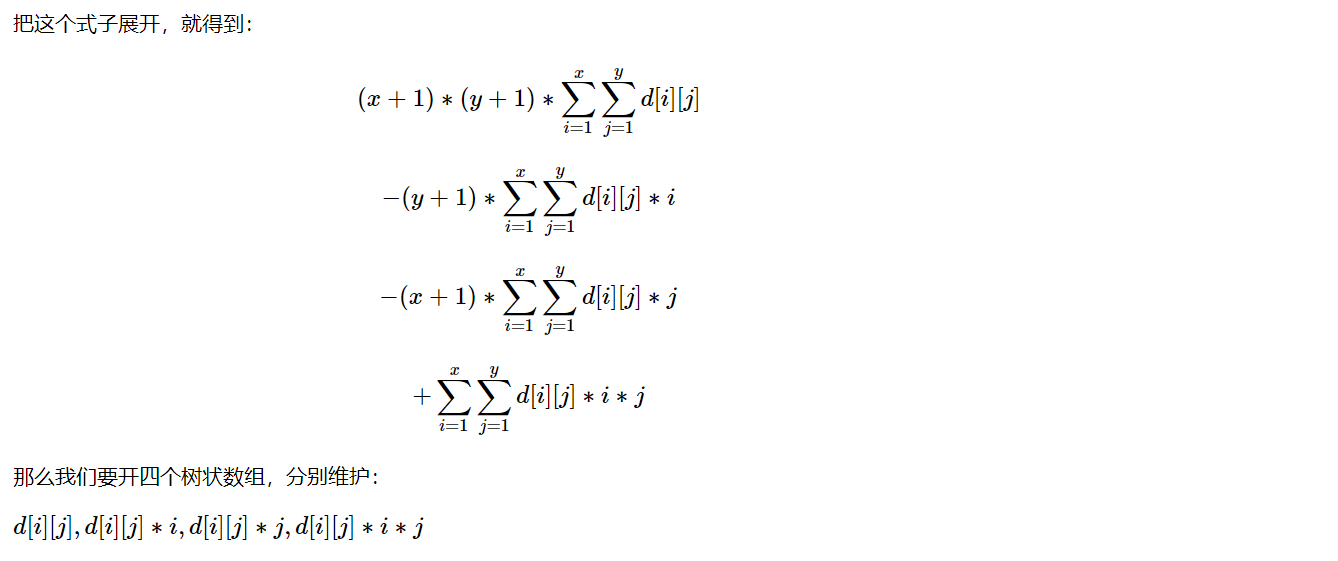
int lowbit(int x)
{
    return x&(-x);
}
void updata(int x,int y,long long z)
{
    for(int i=x;i<=n;i+=lowbit(i)){
        for(int j=y;j<=n;j+=lowbit(j)){
            s1[i][j]+=z;
            s2[i][j]+=x*z;
            s3[i][j]+=y*z;
            s4[i][j]+=x*y*z;
        }
    }
}
long long sum(int x,int y)
{
    long long res=0;
    for(int i=x;i>0;i-=lowbit(i)){
        for(int j=y;j>0;j-=lowbit(j)){
            res+=(x+1)*(y+1)*s1[i][j]-(y+1)*s2[i][j]-(x+1)*s3[i][j]+s4[i][j];
        }
    }
    return res;
}
void solve()
{
    updata(x1,y1,1);
    updata(x2+1,y1,-1);
    updata(x1,y2+1,-1);
    updata(x2+1,y2+1,1);
    printf("%lld\n",sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1));
}