【NeuralScale】2020-CVPR-NeuralScale: Efficient Scaling of Neurons for Resource-Constrained Deep Neural Networks-论文阅读
NeuralScale
2020-CVPR-NeuralScale: Efficient Scaling of Neurons for Resource-Constrained Deep Neural Networks
来源: ChenBong 博客园
- Institute：National Chiao Tung University
- Author：Eugene Lee、Chen-Yi Lee (H40)
- GitHub：https://github.com/eugenelet/NeuralScale
- Citation：3
Introduction
提出了一种按照各层的敏感性, 进行layer-wise的缩放最终达到目标参数量的方法, 区别于uniform的缩放。
Motivation
Contribution
Method
进行 P个 epoch的模型预训练, 在预训练模型的基础上开始迭代剪枝
每次迭代剪枝后, 每一层可以获得一个数据点: \(\xi_{l}=\left\{\tau, \phi_{l}\right\}\) , 其中 \(\tau\) 是模型总参数量, \(\phi_{l}\) 是第 \(l\) 层的 filter个数
N次迭代后, 每一层可以获得N个数据点: \(\boldsymbol{\xi}_{l}=\left\{\left\{\tau^{(n)}, \phi_{l}^{(n)}\right\}_{n=1}^{N}\right\}\)
迭代filter剪枝直到 filter总数 < 原始 filter总数的 \(\epsilon=0.05\) 时, 结束剪枝
将每一层的数据点 \(\boldsymbol{\xi}_{l}\) 画出来, 就得到每一层 filter个数 关于 总参数量的敏感性曲线:
对曲线进行函数拟合:
\(\phi_{l}\left(\tau \mid \alpha_{l}, \beta_{l}\right)=\alpha_{l} \tau^{\beta_{l}}\) ,
\(\ln \phi_{l}\left(\tau \mid \alpha_{l}, \beta_{l}\right)=\ln \alpha_{l}+\beta_{l} \ln \tau\)
所有层的 layer-wise filter数量记为: \(\Phi(\tau \mid \Theta)=\{\phi_1, \phi_2, ..., \phi_l,\}\) , \(\Theta=\{\alpha_1, \beta_1, \alpha_2, \beta_2, ..., \alpha_l, \beta_l\}\)
得到各层的拟合函数 \(\Phi(\tau \mid \Theta)=\{\phi_1, \phi_2, ..., \phi_l,\}\) 以后, 为了得到目标参数量 \(\hat \tau\) 下的 layer-wise filter数量, 只需要将 \(\hat \tau\) 代入 \(\Phi(\hat\tau \mid \Theta)\) , 即可获得layer-wise filter数量
但此时的模型的实际总参数量 \(h(f(\boldsymbol{x} \mid \boldsymbol{W}, \boldsymbol{\Phi}(\hat{\tau} \mid \boldsymbol{\Theta})))\) 与 目标 \(\hat \tau\) 存在差距, 作者提出了, 从初始化 \(\tau=\hat\tau\) 开始, 对 \(\tau\) 进行梯度下降, 找到一个合适的 \(\tau\) , 使得模型实际总参数量 \(h(f)\) 精确等于 \(\hat \tau\) , 作者将这个过程称为 Architecture Descent
Experiments
Setup
- GPU: single 1080ti
- CIFAR10 / CIFAR100
- pre-trian: 10epoch
- 迭代剪枝
- fine-tune?
- 300 epochs
- lr=0.1, decay by 10 at 100, 200, 250 epoch
- weight decay=\(5^{-4}\) , ≈0.0016
- TinyImageNet
- pre-trian: 10epoch
- 迭代剪枝
- fine-tune?
- 150 epochs
- lr=0.1, decay by 10 at 50, 100 epoch
- weight decay=\(5^{-4}\) , ≈0.0016
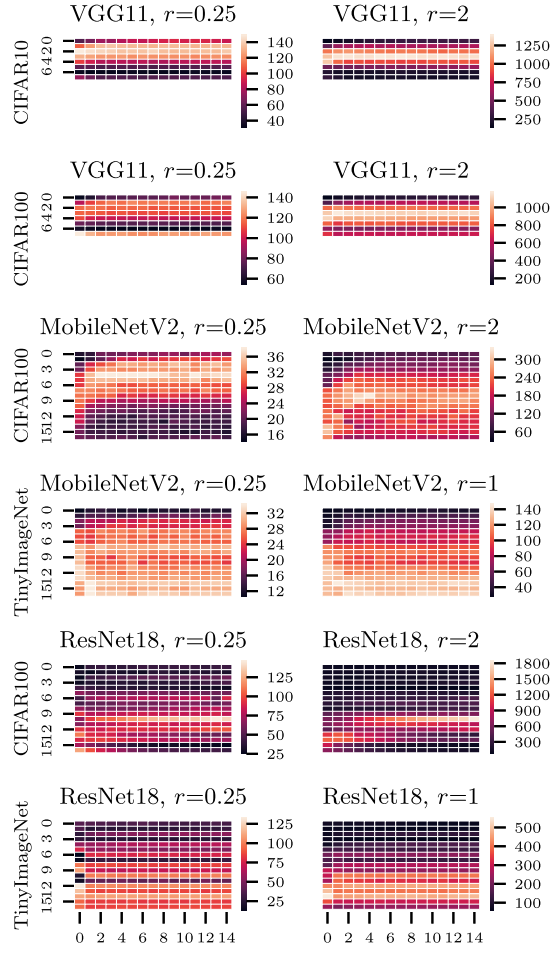
Importance of Architecture Descent
横轴表示 \(\tau\) 的SGD迭代次数, 纵轴表示层数, 颜色表示该层的卷积核个数:
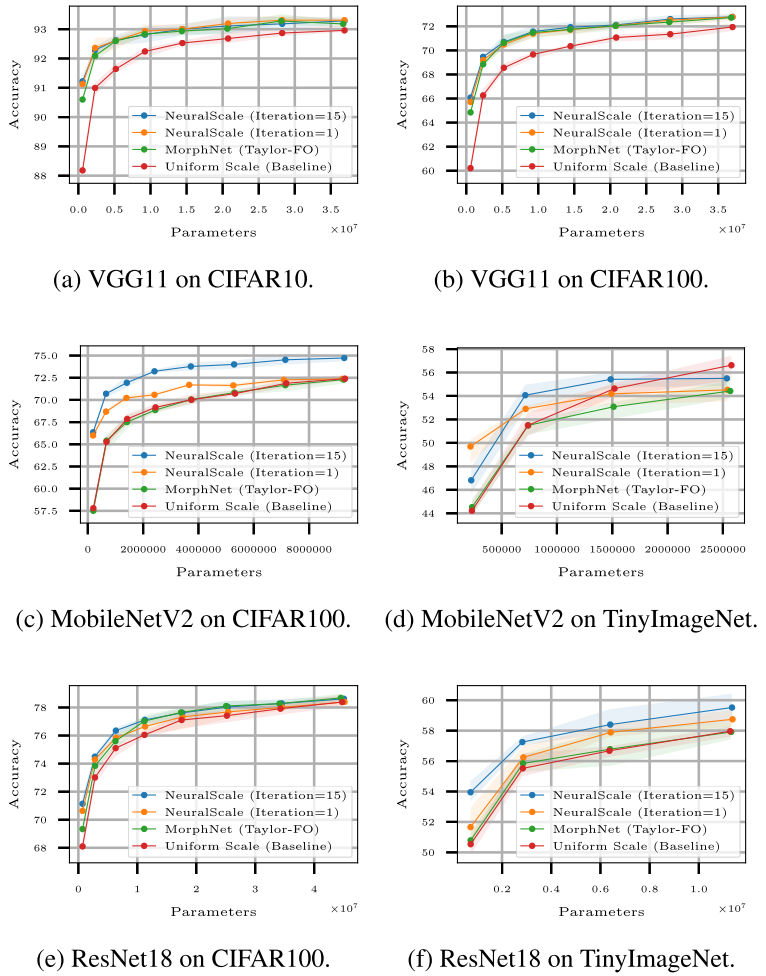
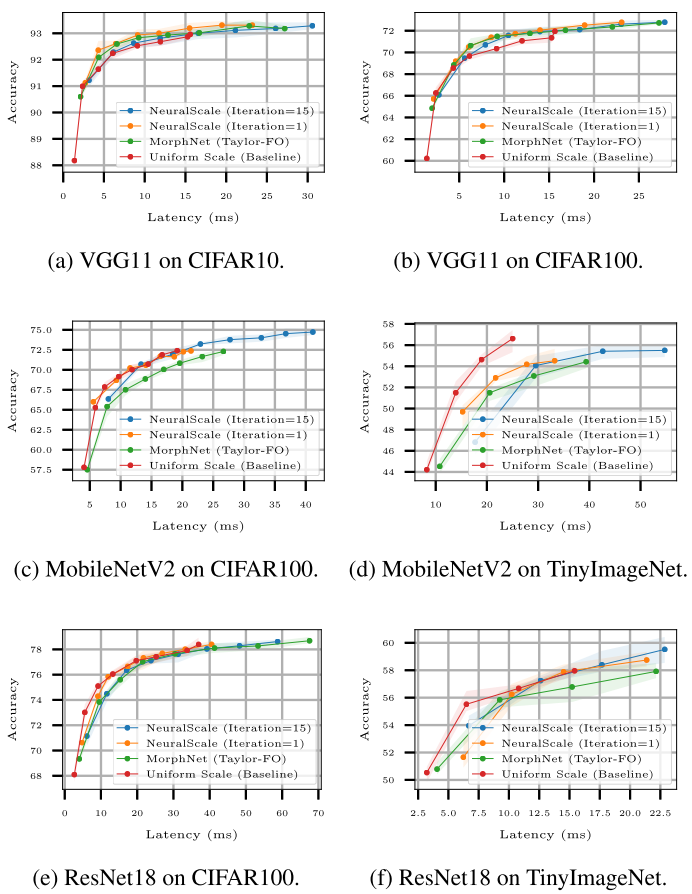
Benchmarking of NeuralScale
param vs acc
latency vs acc
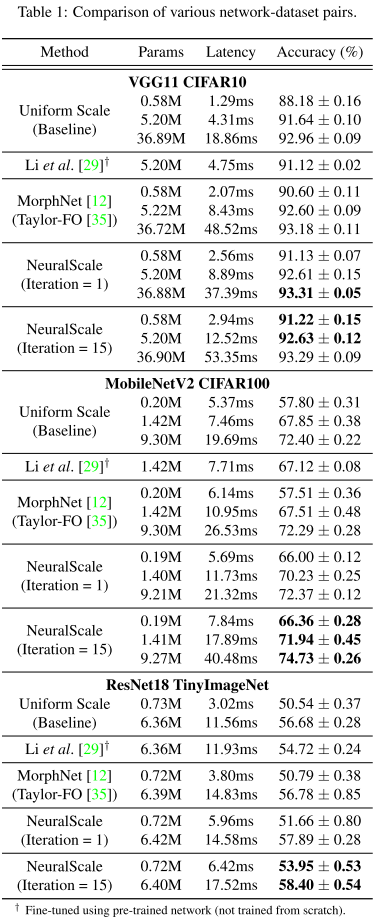
main result
