【AWN】2020-CVPRw-Any-Width Networks-论文阅读

AWN

2020-CVPRw-Any-Width Networks

来源：ChenBong 博客园

• Institute：University of North Carolina at Chapel Hill
• Author：Thanh Vu, Marc Eder, True Price, Jan-Michael Frahm (H 54)
• GitHub：https://github.com/thanhmvu/awn
• Citation：/

Introduction

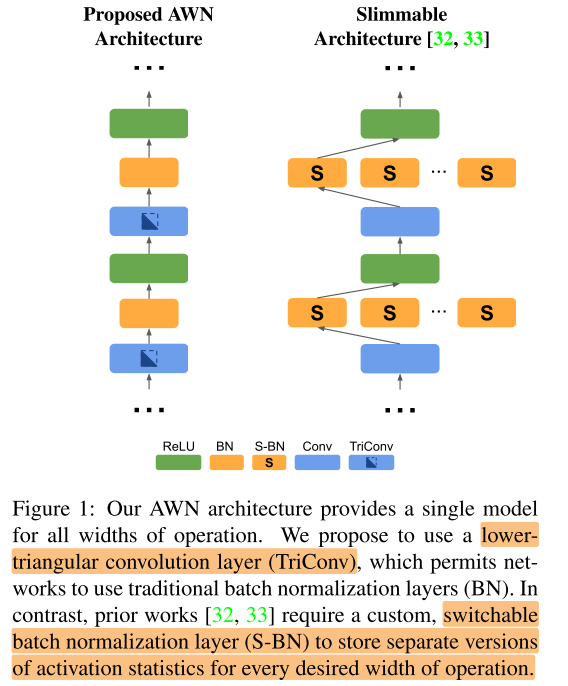
Motivation

slimmable network工作中存在的问题: 每个宽度的网络都需要各自的bn统计量, 之前的2个解决方法:

• 在训练过程中就设置私有bn (SNet, 增加存储开销, 在宽度个数不多的情况下不明显, 在宽度个数多的时候e.g. 20 widths on MB V2, 增加18.5%的model size)
• 训练后的bn校正 (USNet, MutualNet 等其他one-shot nas的标配做法; 需要post process的过程)

针对这2个方案存在的问题, 提出了一种下三角卷积层, 替换常规卷积层, 实现不增加存储开销, 无需post process, 训练完毕后可以在任意宽度进行推理

Contribution

Method

不同宽度的bn层需要重新校正的原因是什么?

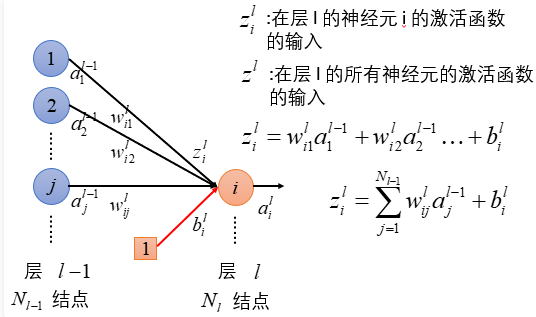
以MLP为例

\(\boldsymbol{y}_{i}^{\left\{m_{i}\right\}}=\boldsymbol{W}_{i}^{\left\{m_{i} \times m_{i-1}\right\}} \boldsymbol{x}_{i}^{\left\{m_{i-1}\right\}}\)

第 \(i\) 层的全连接层神经元个数是 \(m_i\) , 上一层全连接层神经元个数是 \(m_{i-1}\)

当乘上宽度系数 \(\alpha\) 后, 该层的神经元个数变为 \(k_{i}=\alpha m_{i}\)

例如, k=1时:

\(\begin{aligned} \boldsymbol{y}^{\{1\}} &=\boldsymbol{W}^{\{1\}} \boldsymbol{x}^{\{1\}} \\\left[y_{1}\right] &=\left[w_{11}\right]\left[x_{1}\right] \\ &=\left[w_{11} x_{1}\right] \end{aligned}\)

k=2时:

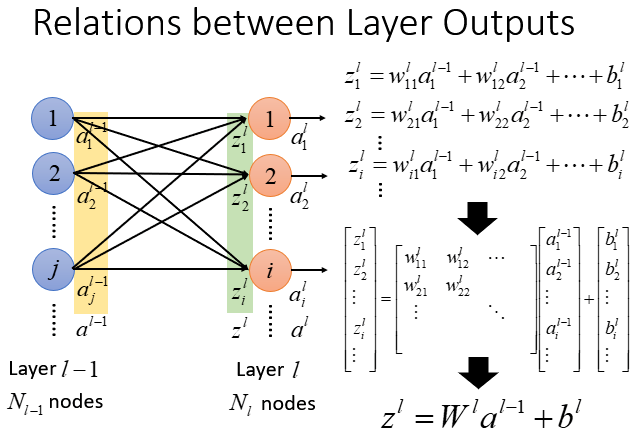
\(\begin{aligned} \boldsymbol{y}^{\{2\}} &=\boldsymbol{W}^{\{2\}} \boldsymbol{x}^{\{2\}} \\\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right] &=\left[\begin{array}{ll}w_{11} & w_{12} \\ w_{21} & w_{22}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \\ &=\left[\begin{array}{l}w_{11} x_{1}+w_{12} x_{2} \\ w_{21} x_{1}+w_{22} x_{2}\end{array}\right] \end{aligned}\)

使用bn层后, 全连接层的输出 \(\mathcal y\) 会按照累积的统计量 mean, var进行 normalization后 再作为下一层的输入

以只有一个样本为例, 对于不同宽度的全连接层:

\(y_{1}=\left\{\begin{array}{ll}w_{11} x_{1} & \text { if } k=1 \\ w_{11} x_{1}+w_{12} x_{2} & \text { if } k=2 \\ \ldots & \ldots\end{array}\right.\)

\(\begin{aligned} \mathbb{E}\left[y_{1}^{\{1\}}\right] &=\mathbb{E}\left[w_{11} x_{1}\right]=\mu_{1}^{\{1\}} \\ \mathbb{E}\left[y_{1}^{\{2\}}\right] &=\mathbb{E}\left[w_{11} x_{1}+w_{12} x_{2}\right] \\ &=\mathbb{E}\left[w_{11} x_{1}\right]+\mathbb{E}\left[w_{12} x_{2}\right] \\ &=\mu_{1}^{\{1\}}+\mathbb{E}\left[w_{12} x_{2}\right] \end{aligned}\)

除非 \(\mathbb{E}\left[w_{12} x_{2}\right]=0\) , \(y^{\{1\}}\) 和 \(y^{\{2\}}\) 才能服从相同的分布

即简单地设 \(W_{ij}=0\) 当 \(i<j\) , 得到 triangular convolution/fc layer

用 triangular convolution layer 替换原始的conv/fc layer的网络称为 AWNs

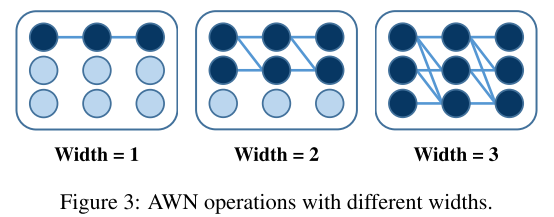
对于AWNs, 有2种训练方式:

• AWN: k-width training (和 S-Net 相同)
• AWN+RS: random sample training (和US-Net相同)

第 \(i\) 层的全连接层的神经元个数是 $$

Experiments

LeNet-3C1L on MNIST

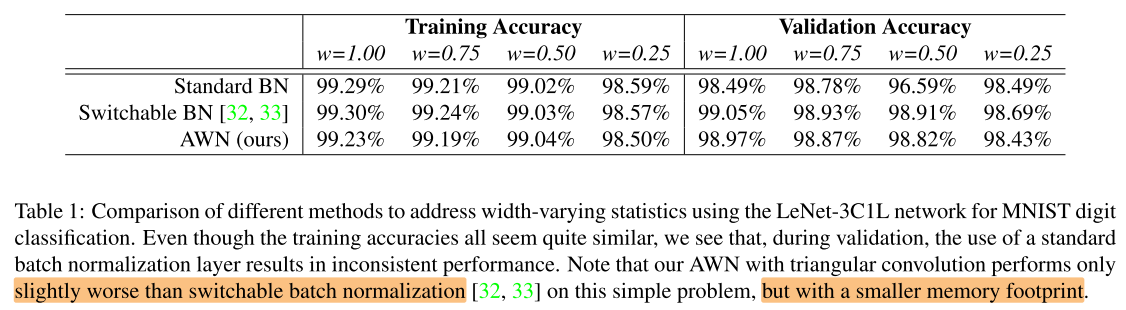
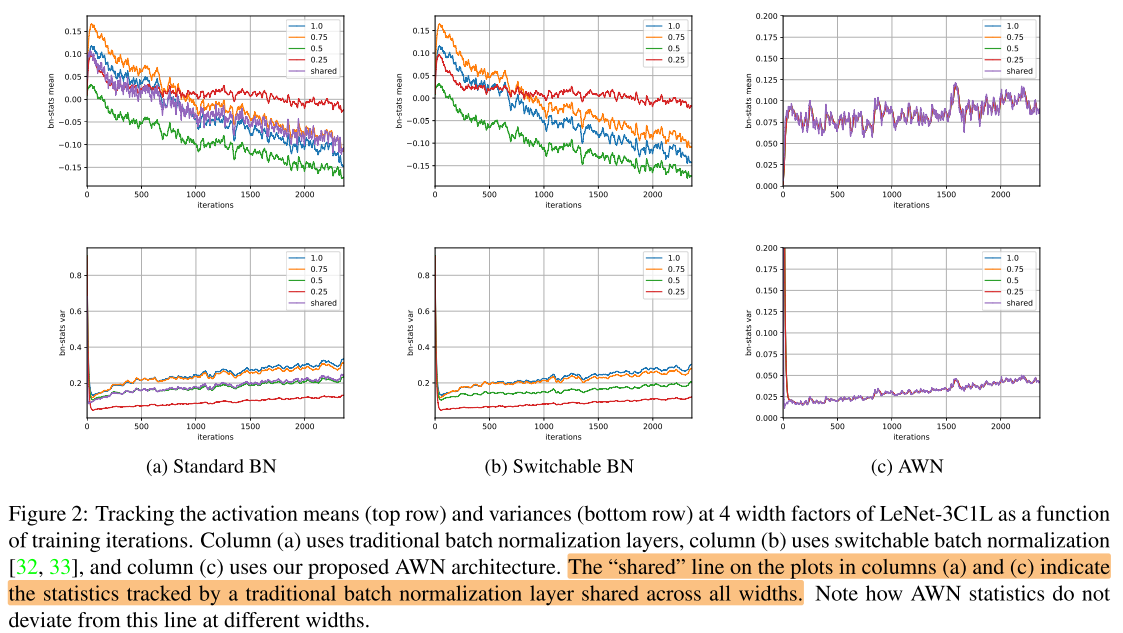
setup

由于AWNs会减少接近一半的参数量, 一次训练中AWNs使用的网络宽度扩大了 \(\sqrt 2\) 倍, 以保持参数量和原网络一致

• SGD, momentum=0.9, batch_size=128
• LeNet-C31L
  • S-Net, US-Net, AWN, AWN+RS
  • lr: 0.01 (decay by 0.1 at 50%, 75% epochs)
  • FashionMNIST
    • 20 epochs
    • weight_decay=0.0
  • CIFAR-10/CIFAR-100
    • 100 epochs
    • weight_decay=5e-4
• MobileNetV2
  • S-Net, US-Net
    • CIFAR-10/CIFAR-100
      • 100 epochs
      • weight_decay=5e-4
      • lr=0.1 (decaying linearly)
  • AWN
    • CIFAR-10
      • 700 epochs
      • weight_decay=5e-4
      • lr=0.02 (decay by 0.2 at 500, 600 epochs)
    • CIFAR-100
      • 100 epochs
      • weight_decay=5e-4
      • lr=0.1 (?)
  • AWN+RS
    • CIFAR-10
      • 350 epochs
      • weight_decay=?
      • lr=0.01 (decay by 0.1 at 250, 300 epochs)
    • CIFAR-100
      • 1050 epochs
      • weight_decay=1e-3
      • lr=0.01 (decay by 0.1 at 750, 900 epochs)

main results

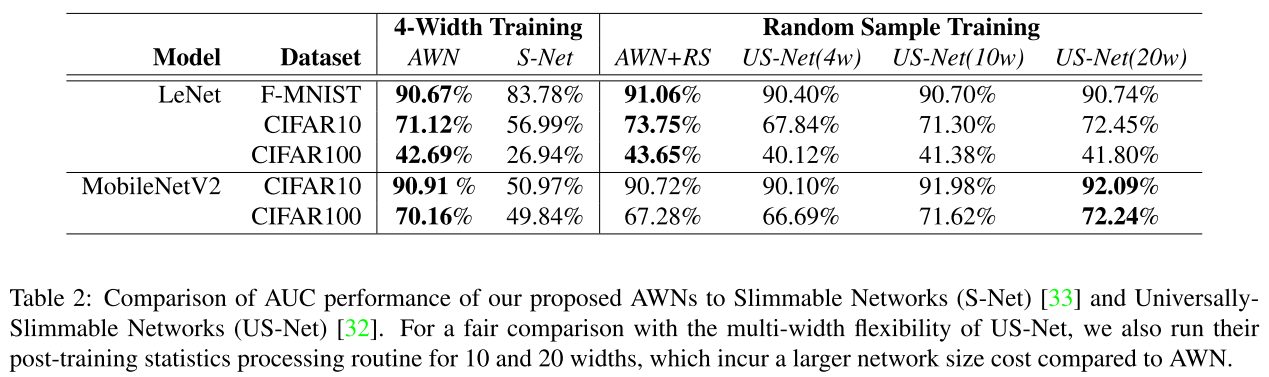
Area Under the Curve(AUC)

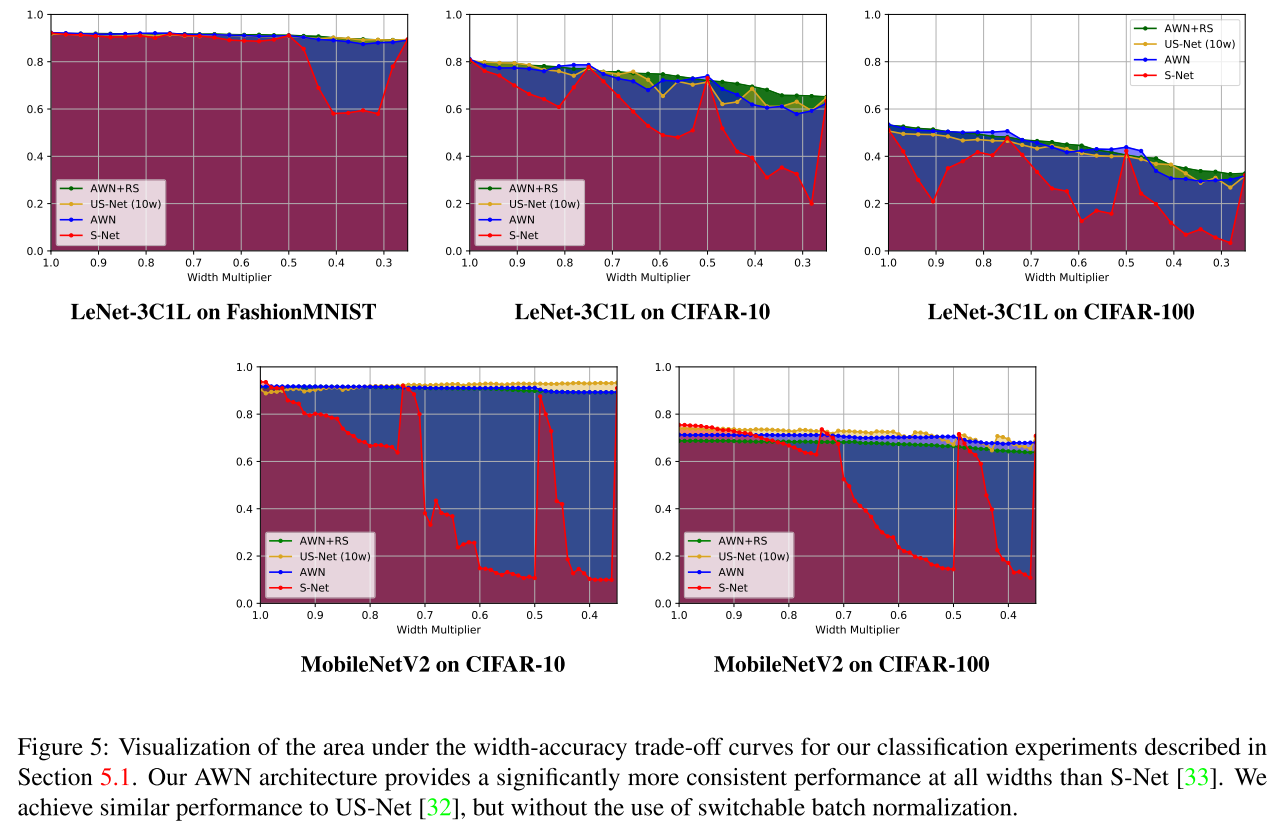
Conclusion

Summary

pros:

• 提出了一种天然支持不同宽度, 不改变bn统计量的卷积/全连接层, 下三角权重矩阵

cons:

• 扩大了网络的宽度, 一定程度上是不公平的比较
• MobileNetV2上的实验设置很复杂, 有的epoch数特别大, 其他参数像是精心选择过, 且代码只开源了 lenet cifar10
• 估计在大数据集上效果不佳

Question:

• 使用下三角的conv/fc替代原始conv/fc后, 参数量计算量都减半? 宽度扩大为原来的 \(\sqrt 2\) 倍, 参数量, 计算量都恢复到和原网络一致?

Reference

Thanh Vu (thanhmvu.com)