【Fast Scaling】2021-CVPR-Fast and Accurate Model Scaling-论文阅读
Fast Scaling
2021-CVPR-Fast and Accurate Model Scaling
来源: ChenBong 博客园
- Institute:Facebook AI Research (FAIR)
- Author:Piotr Dollar Mannat Singh Ross Girshick
- GitHub:https://github.com/facebookresearch/pycls
- Citation: /
Introduction
RegNet的后续工作
通过对小模型进行缩放(主要是放大)来得到一系列大模型, 从而获得一系列性能优秀的模型族。
对模型缩放,在增加同样的计算量下,可以有不同的不同的缩放策略(例如要对一个300M的模型放大到400M,这增加的100M计算量可以全部增加在宽度w/深度d/分辨率r的维度上,也可以在不同维度上都分配一部分,多个维度同时缩放),且不同的缩放策略带来的性能增益acc,开销增益 flops/latency/epoch time 都不尽相同。
我们希望通过研究不同的缩放策略,来获得一种通用的性能增益多,但开销增益少的快速缩放策略。
我们通过实验证明了不同的缩放策略产生的不同flops的模型有着相似的性能增益,但在开销增益上有着较大的区别。在总结了大量缩放规则的基础上,提出了一种简单的复合缩放策略,在模型宽度的维度上缩放多,在深度/分辨率的维度上缩放少。
Motivation
- 模型缩放是获得一组不同规模下的模型族的方法之一,具有简单快速的特点(相比nas,手工设计等)
- 对于优化小模型(手工设计,随机搜索,nas)是很容易的,但如果获得一个优化大模型就是一个很大的问题
- 模型缩放是从优质小模型快速获得一组优质大模型的一种简单快速的方法
- 虽然目前已经有了一些多维度的缩放策略(e.g. EfficientNet),但主要集中在 flops-acc 的 tradeoff 上,很少关注部署中的因素(e.g. 2个具有相同flops的模型的 latency 可能会有很大的区别)
- 且之前的工作对不同维度之间的定量的 tradeoff 分析还不够
- 如何设计一种既能优化模型精度,又能优化 latency (性能增益多,开销增益少)的缩放策略?
Contribution
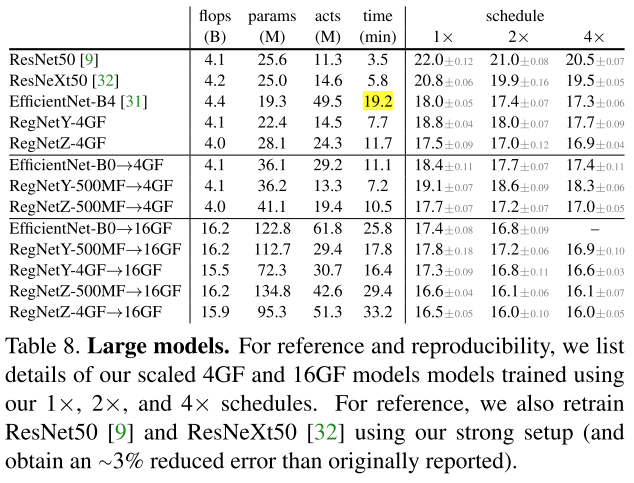
- 观察:
- 不同的缩放策略,可以再相同的flops下产生精度acc相近的模型(图1左上);
- 但缩放后模型的latency却有很大的不同(图1右下)
- 从flops=f 缩放到flops=sf,只缩放w,latency 的增长速度 \(O(\sqrt s)\),复合缩放的增长速度 \(O(s)\)
- 图1左下,右下:在一定范围内,缩放模型的 latency-activation 的相关性比 latency-flops的相关性更强,因此我们可以用activation作为预测latency的proxy
- ps. activation的定义:conv的output feature map中的元素数量
- 基于分析和观察,我们提出了一种 fast scaling 的缩放策略,由一个单一参数 \(\alpha, (0<<\alpha<1)\) 控制,由 fast scaling 缩放得到的模型又快又准,通过 fast scaling 可以获得与sota相当的大模型,但速度更快(e.g. RegNetY-4GF fast scaling to 16GF,获得比EfficientNet-B4更快,更准,占用内存更少的模型)
Related Work
- Manual network design
- Automated network design(NAS)
- Design space design
- Network scaling
- Going bigger
Method
Complexity of Scaled Models
本节研究了不同维度的缩放对模型的3个复杂度 metric 的影响
Complexity Metrics
度量模型复杂性该用什么指标?
- 模型的3个属性:\(flops(f), parameters(p), activations(a)\)
- parameter与输入分辨率无关,不能反映模型容量或latency,因此不作为复杂度度量的主要指标
- 因此我们将flops作为主要的复杂性度量指标,关注activation与latency的关系
Network Complexity
- 模型层的类型很多(bn,pool,activation),但这些层一般都与conv的数量成正比,且计算也主要集中在conv层中,因此我们认为conv层的Complexity是整个network complexity的proxy
- 考虑一个conv层:cin × cout × k × k,cin=cout=w(设一个stage每个conv layer的cout都相同), input feature map: r × r × w,因此一个conv的复杂度为: \(f=w^2r^2k^2,\ p=k^2w^2,\ a=wr^2\) ,
- 由于k不参与scale,不是一般性地设k=1,因此一个conv的复杂度为: \(f=w^2r^2,\ p=w^2,\ a=wr^2\) ,
- 每个stage有d个conv layer,因此一个stage的复杂度为: \(f=dw^2r^2,\ p=dw^2,\ a=dwr^2\)
- 简单起见,我们对每个stage使用相同的缩放策略,因此对stage复杂度的分析与整个网络的复杂度相同
Complexity of Simple Scaling
simple scaling:单一维度(d/w/r)的缩放,从 \(flops=f\) 缩放到 \(flops=sf\)

3种 simple scaling 中,flops的增益的相同的,但p和a的增益是不同的:
- 在w维度上缩放对 activations 的增益是最少的
- 在r维度上缩放对 parameters 的增益是最少的
Complexity of Compound Scaling
Compound Scaling:复合缩放,在多个维度上同时缩放,从 \(flops=f\) 缩放到 \(flops=sf\)
在之前的工作中证明了复合缩放可以比单一维度缩放获得更高的精度
将增加的倍数 s 均匀分配到多个维度上:

EfficientNet中的经验法则dwr scale的比例分别为1.2,1.1,1.5;和表2中在3个维度上均匀分配的比例相当 \(s=2 (\sqrt[3]{s}=1.26,\ \sqrt[6]{s}=1.12)\) ,因此我们将3个维度上的均匀缩放作为 Compound Scaling 的代表进行分析
Complexity of Group Width Scaling
很多sota模型都依赖 group conv 或 depthwise conv(depthwise 是g=1的 gruop conv)因此我们对g的维度也进行探究,模型复杂度为 \(f=wgr^2, p=wg, a=wr^2\)
为了获得和缩放常规卷积相当的结果 \(f=w^2r^2\) ,对于group conv,我们同步缩放w和g(但对于depthwise conv,只缩放w)

Runtime of Scaled Models
本节研究了3个模型复杂度metric与latency的关系
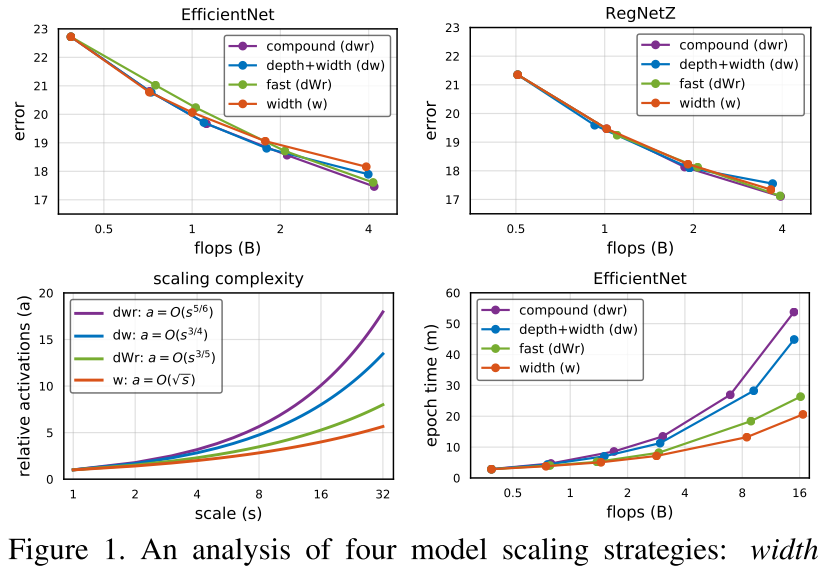
从图2左上,右上可以看出:沿着不同维度缩放模型时,flops和parameters与模型latency的相关性很弱(缩放到相同的flops/parameters,模型latency的差异很大)
从图2左下,右下可以看出:不论沿着什么维度扩展模型(不同的缩放策略),activations与latency的相关性总是很高
Fast Compound Model Scaling
由于activations与latency有很强的相关性,因此我们的目标是设计一种在相同flops下,使得activations增量最小的缩放策略。
根据表1-3的结论,我们知道(相同的flops)在宽度w和组数g上的缩放对 activations 的增量最小(开销增益最小),但只在这2个维度上进行缩放不能达到最好的性能(性能增益不够)。
为了解决这个问题,我们设计了一种 Fast Compound Model Scaling(简称Fast Scaling)的方法,简单来说就是主要在宽度w的维度上扩展,较小地在另外2个维度d/r上扩展(并且在剩下2个维度均匀缩放)。
w维度上的扩展比例由单一参数 \(\alpha\) 决定, \(\alpha\) 为0-1,
- \(\alpha=0\) 就是不在w维度上扩展
- \(\alpha=1/3\) 就是w维度上缩放(带来的flops增量)占总flops增量的1/3,相当于在3个维度均匀缩放
- \(\alpha=1\) 就是只在w维度上扩展
一个stage的复杂度为: \(f=dw^2r^2,\ p=dw^2,\ a=dwr^2\)
根据 \(\alpha\) 定义3个维度的缩放倍数:
中间系数: \(e_{d}=\frac{1-\alpha}{2}, \quad e_{w}=\alpha, \quad e_{r}=\frac{1-\alpha}{2}\)
缩放倍数: \(d^{\prime}=s^{e_{d}} d, \quad w^{\prime}=\sqrt{s}^{e_{w}} w, \quad r^{\prime}=\sqrt{s}^{e_{r}} r .\)

多维度均匀缩放:

由于主要在w维度上缩放,因此我们实验的范围是 \(1/3<\alpha<1\)
无特别说明时, \(\alpha=0.8\) ,记为 \(dWr\)
Experiments
Baselines Network
baseline network
- EfficientNet
- RegNetY,RegNetZ
Optimization Settings
Our goal is to enable fair and reproducible results. However, we also aim to achieve state-ofthe-art results. This creates a tension between using a simple yet weak optimization setup (e.g., [22]) versus a strong setup that yields good results but may be difficult to reproduce (e.g., [31]).
不同baseline/不同模型大小配置不同,会公开训练配置
Simple and Compound Scaling
EfficientNet
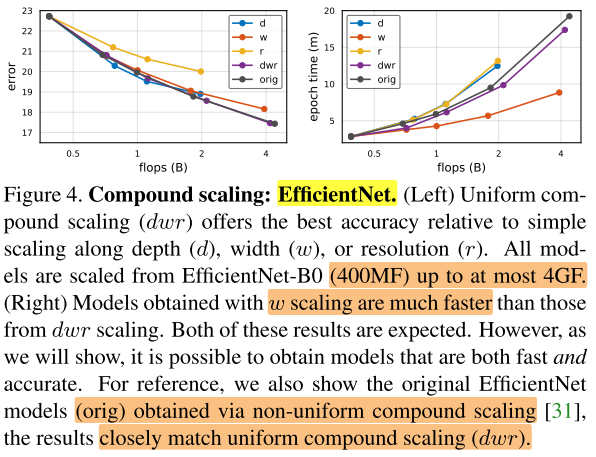
- 和预期的一样,dwr的缩放方式(性能高,速度慢),w的方式(性能低,速度快)。说明介于这之间有个一个tradeoff
- EfficientNet原始的非均匀缩放在acc-latency上与均匀缩放相当(但均匀缩放是更简单的,不需要仔细调参)
RegNet
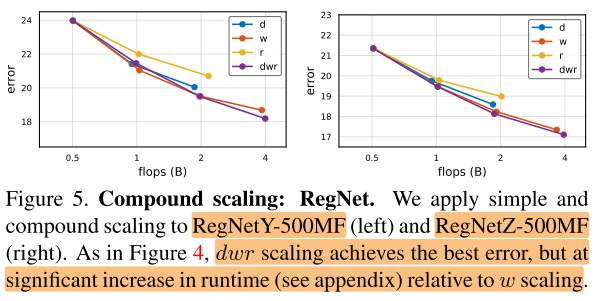
- 在RegNet上的实验的结果类似,dwr的缩放方式(性能高,速度慢),w的方式(性能低,速度快)
Fast Scaling
上面的实验证明了 dwr缩放 \((\alpha=1/3)\) 和 w缩放 \((\alpha=1)\) 之间存在tradeoff,特别地,我们将 \(\alpha=0.8\) 定义为Fast Scaling,记为dWr
EfficientNet
EfficientNet在不同 \(\alpha\) 缩放下的 err 和 latency:
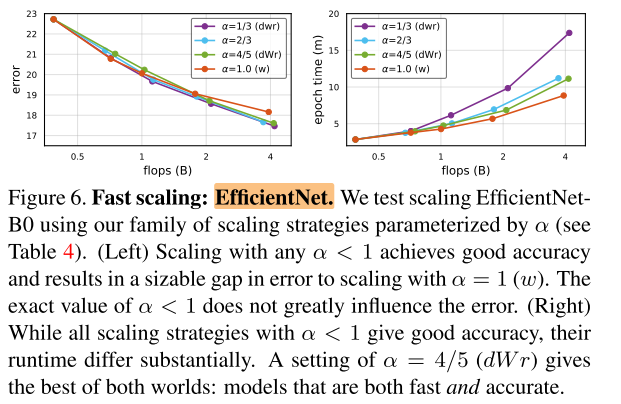
左图:在不同的 \(\alpha<1\) 缩放下,精度都相当,都高于仅在w上缩放 \(\alpha=1\) ;
右图:dWr 缩放比均匀缩放 dwr 的 latency 快得多(dwr和Effi ori接近,因此dWr比Effi快得多),已经接近w缩放
RegNet
RegNet上的结果也是相似的:
RegNet在不同 \(\alpha\) 缩放下的 err :
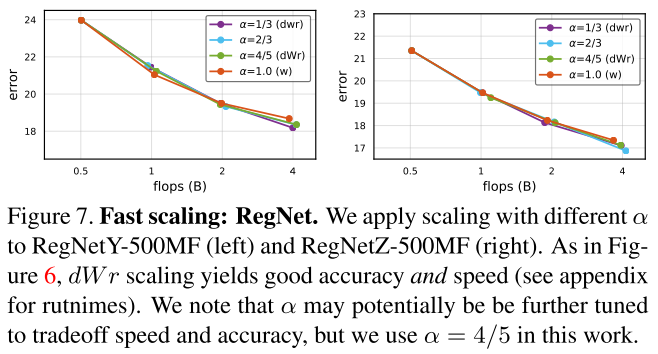
图7:在不同的 \(\alpha<1\) 缩放下,精度都相当,都高于仅在w上缩放 \(\alpha=1\) ;
RegNet在不同 \(\alpha\) 缩放下的 latency :
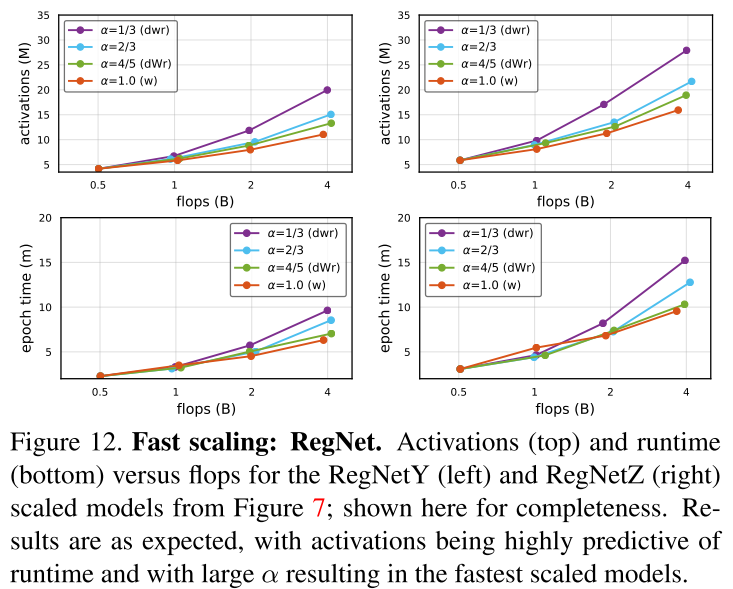
图12下:dWr 缩放比均匀缩放 dwr 的 latency 快得多,已经接近w缩放
Scaling versus Search

- 直接随机搜索的4G RegNet 模型比从小模型放大的要好0.6/0.1个点,且有着更少的参数量。说明
- 对最优的小模型做Fast Scaling不一定能得到一个最优的大模型
- 直接放大模型存在无法对不同stage重新分配block的限制
- 但当目标模型大小非常大(16GF)时,快速缩放策略还是有用的,折中的策略是搜索中等模型,再 Fast Scaling 放大得到大模型
Comparison of Large Models
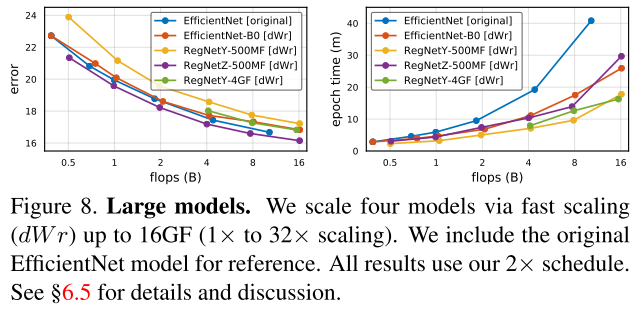
- 图8左:缩放性能的一致性,缩放不改变模型的相对性能,RegNetZ获得了最好的性能
- 图8右:dWr缩放得到的模型都比 Effi ori 快得多
- 对RegNetY使用折中策略缩小了,Y/Z之间的差距
- RegNetY-4GF→16GF 比EfficientNet-B4使用的内存更少,速度快4了倍