【ManiDP】2021-CVPR-Manifold Regularized Dynamic Network Pruning-论文阅读
ManiDP
2021-CVPR-Manifold Regularized Dynamic Network Pruning
来源：ChenBong 博客园
- Institute：PKU，Huawei Noah
- Author：Yehui Tang，Yunhe Wang
- GitHub：/
- Citation：
Introduction
动态剪枝，对不同的输入样本使用不同的剪枝子网，实现了更高的精度和加速比（FLOPs剪枝率）。动态剪枝的核心问题是如何为不同样本分配不同的子网，即如何学习一个从样本到子网的映射函数。本文考虑了样本和模型的复杂度和相似度的对齐，从而使模型更好地将样本映射到对应的子网。
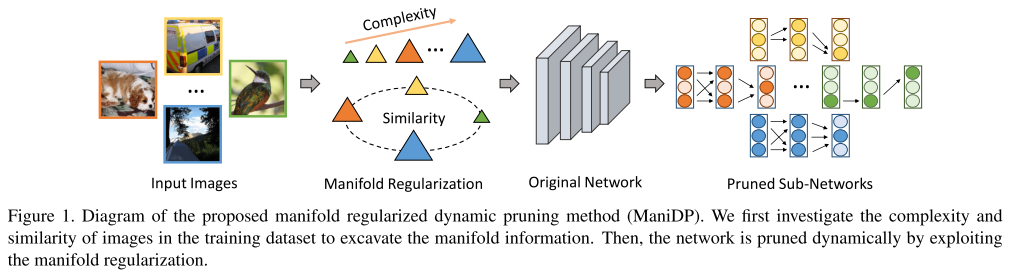
动态网络的方法保留了完整的网络结构和参数，因此网络参数其实没有减少；且 FLOPs 对不同的样本是不同的，因此本文汇报的是测试集上所有样本的平均 FLOPs。
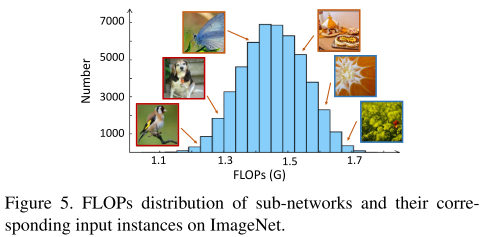
Related Work
- Channel Pruning
- Static Pruning：GAL，HRank
- Dynamic Pruning
- Weight Pruning
Motivation
- 之前的静态剪枝方法不考虑输入的差异，用同样的静态剪枝网络处理所有输入
- 卷积核的重要性是 highly input-dependent 的，即不同输入对应的冗余卷积核应该是不同的；这其实就是动态网络的思想，动态网络是不同样本选择不同的结构（宽度，深度），本文的动态剪枝是不同样本剪掉不同的卷积核（宽度）
- 之前的动态网络/剪枝方法没有利用不同样本之间的关系，例如：简单的样本使用简单的子网（复杂度对齐）；相似的样本使用相似的子网（相似度对齐）
Contribution
- 考虑了（样本，模型）复杂度和相似度对应关系的一种动态剪枝新范式
Method
静态剪枝
优化目标：
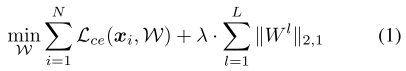
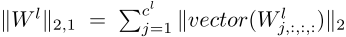
传统的动态剪枝
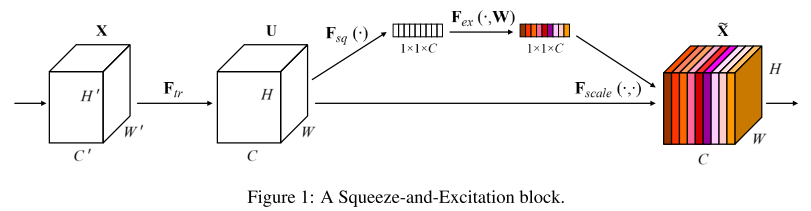
每一层都有一个control module \(\mathcal{G}^{l}\) （如SE：avgpool-fc-sigmoid），根据上一层的输出 feature map，来计算当前层的输出通道显著性vector： \(\boldsymbol{\pi}^{l}\left(\boldsymbol{x}_{i}, \mathcal{W}\right)=\mathcal{G}^{l}\left(F^{l-1}\left(\boldsymbol{x}_{i}\right)\right) \in \mathbb{R}^{c^{l}}\)
通道显著性vector \(\pi^l\) 再过一个阈值 \(\xi^{l}\) （大于阈值的取1，否则取0），得到该层输出通道的稀疏mask：\(\hat{\boldsymbol{\pi}}^{l}\left(\boldsymbol{x}_{i}\right)=\mathcal{I}\left(\boldsymbol{\pi}^{l}\left(\boldsymbol{x}_{i}\right), \xi^{l}\right)\)
这里的阈值 \(\xi^{l}\) 需要 layer-by-layer 地设置，进而决定 layer-wise 的剪枝率，某一层的阈值越大，该层的剪枝率越大。
前向过程：
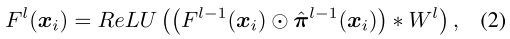
优化目标：
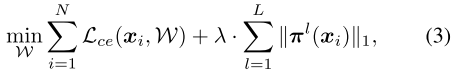
Manifold 动态剪枝
传统的动态剪枝虽然考虑了输入的差异来选择不同的子网，但只利用了 input 本身的信息，还有其他维度的信息可以进一步挖掘，例如：简单的样本分配简单的子网（复杂度对齐）；相似的样本分配相似的子网（相似度对齐）。
manifold 假说：input samples 到其对应子网的映射函数，在高维空间下应是平滑的，即 input samples 之间的关系，在对应的子网上也依然要保持。（复杂度空间，相似度空间）
多维信息可以有效地 regularize 解空间中的 instance-subnetwork pairs ，其实就是说 Manifold 动态剪枝 可以更好地学习一个 instance-subnetwork 的映射函数，从而更好地为每个 instance 分配对应的子网。
Instance Complexity 样本复杂度
intuition：不同难度的样本预测难度是不同的，困难的样本（小目标，背景混乱等）需要更大的 model capacity，更强的 model representation ability，来更有效地提取信息。
这个 intuition 说明了样本之间还存在一个一维的 complexity space，可以利用该空间的信息帮助学习一个更好的 instance-subnetwork 映射函数。
首先用 metric 来衡量 instances 和 sub-networks 的复杂度，然后用自适应的函数来对齐实例之间和子网之间的复杂度关系。
- instances复杂度：用 Loss 来衡量当前输入实例的复杂度，Loss小说明当前实例简单，Loss大说明实例复杂
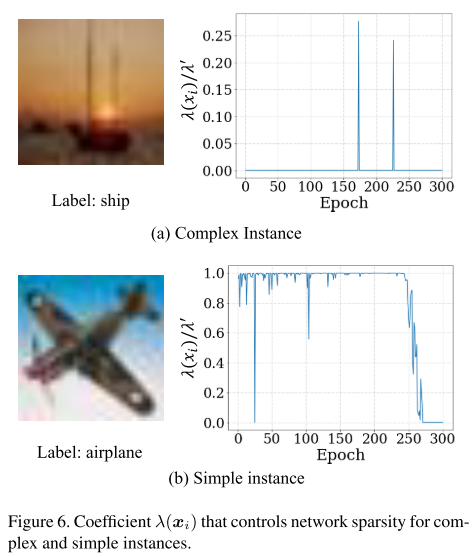
- subnetwork复杂度：用通道显著性vector \(\pi^{l}({x}_{i})\) 来衡量子网的复杂度，根据公式(3)， \(\pi^{l}({x}_{i})\) 的稀疏性是由系数 \(\lambda\) 来控制的，更大的 \(\lambda\) 会诱导更强的稀疏性。
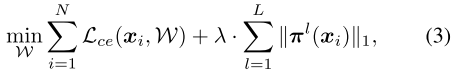
因此，当某个实例的 Loss 下降时，对应的稀疏惩罚系数 \(\lambda\) 要提高，反之亦然。极端情况下，当一个样本 Loss 很大时（over complex），对应的稀疏惩罚系数 \(\lambda=0\)
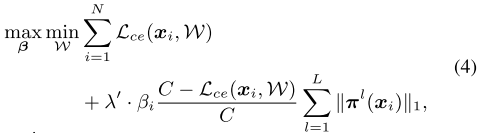
\(\lambda'\) 是超参，对所有实例共享； \(C\) 是预先定义的阈值，如果某个实例的 Loss > C，则认为该实例 over complex，稀疏惩罚项 \(\beta_i=0\) ，否则 \(\beta_i=1\) ：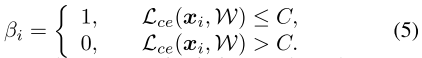
记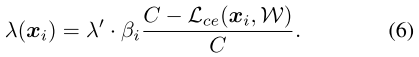 
，其中 \(\lambda(x_i)\) 范围为 \([0, \lambda']\)
公式(4)重写为：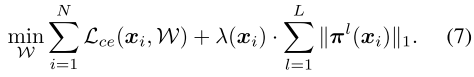
Instance Similarity 样本相似度
intuition：除了复杂度空间，实例之间的相似度也是重要的信息，可以帮助学习一个更好的（instance-subnetwork）映射函数。例如：样本相似，对应分配的子网也要相似。
首先用 metric 来衡量样本相似度，要么用原始图片，要么用中间特征。作者认为中间特征是不同样本更有效的表示（高层的语义信息，在更高维度上的相似度）。
子网的结构可以用每一层的通道显著性 \(\pi^{l}({x}_{i})\) 来编码，通道显著性 \(\pi^{l}({x}_{i})\) 和中间特征都是layer-wise的，因此作者去计算每一层 \(\pi^{l}({x}_{i})\) 相似矩阵 \(T^{l} \in \mathbb{R}^{N \times N}\) 和 中间特征 的相似矩阵 \(R^{l} \in \mathbb{R}^{N \times N}\) ：
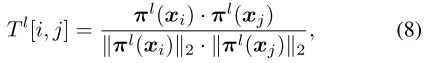
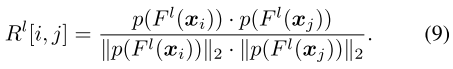，其中 \(p(\cdot)\) 表示平均池化操作
添加相似度Loss：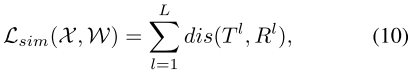
，其中 \(\operatorname{dis}\left(T^{l}, R^{l}\right)=\left\|T^{l}-R^{l}\right\|_{F}\) ，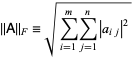
总Loss变为：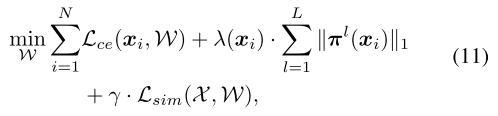
，其中 \(\gamma\) 是超参
设置 layer-wise 剪枝率
通道显著性vector \(\pi^l\) 再过一个阈值 \(\xi^{l}\) （大于阈值的取1，否则取0），得到该层输出通道的稀疏mask：\(\hat{\boldsymbol{\pi}}^{l}\left(\boldsymbol{x}_{i}\right)=\mathcal{I}\left(\boldsymbol{\pi}^{l}\left(\boldsymbol{x}_{i}\right), \xi^{l}\right)\)
这里的阈值 \(\xi^{l}\) 需要 layer-by-layer 地设置，进而决定 layer-wise 的剪枝率，某一层的阈值越大，该层的剪枝率越大。
本文的方法是需要手工设置每一层的阈值 \(\xi^{l}\) 的，而我们一般有的是 layer-wise 剪枝率（本文 layer-wise 剪枝率 follow 之前的动态剪枝工作 FBS），那么如何通过 layer-wise 剪枝率计算 \(\xi^{l}\) ？
以第 \(l\) 层为例，取N个样本，计算第 \(l\) 层的 \(c^l\) 个通道的平均通道显著性，并排序： \(\overline{\boldsymbol{\pi}}^{l}[1] \leq \overline{\boldsymbol{\pi}}^{l}[2] \leq \cdots \leq \overline{\boldsymbol{\pi}}^{l}\left[c^{l}\right]\) ，则阈值 \(\xi^{l}\) 设置为第 \(\lceil\eta c^{l}\rceil\) 个 \(\overline{\boldsymbol{\pi}}^{l}[\cdot]\) ，即 \(\xi^{l}=\boldsymbol{\pi}^{l}\left[\left\lceil\eta c^{l}\right\rceil\right]\)
推理时，只有大于阈值的通道才会被计算，其余的会被跳过，从而减少计算量。
Experiments
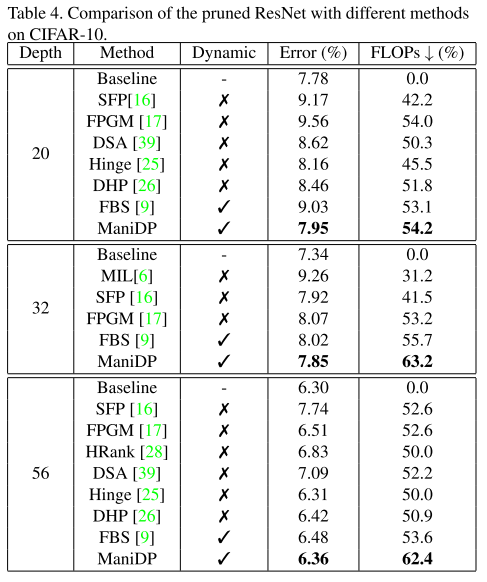
CIFAR10
由于每张图片的FLOPs都是不同的，表格里报告的是整个数据集每张图片的平均FLOPs剪枝率
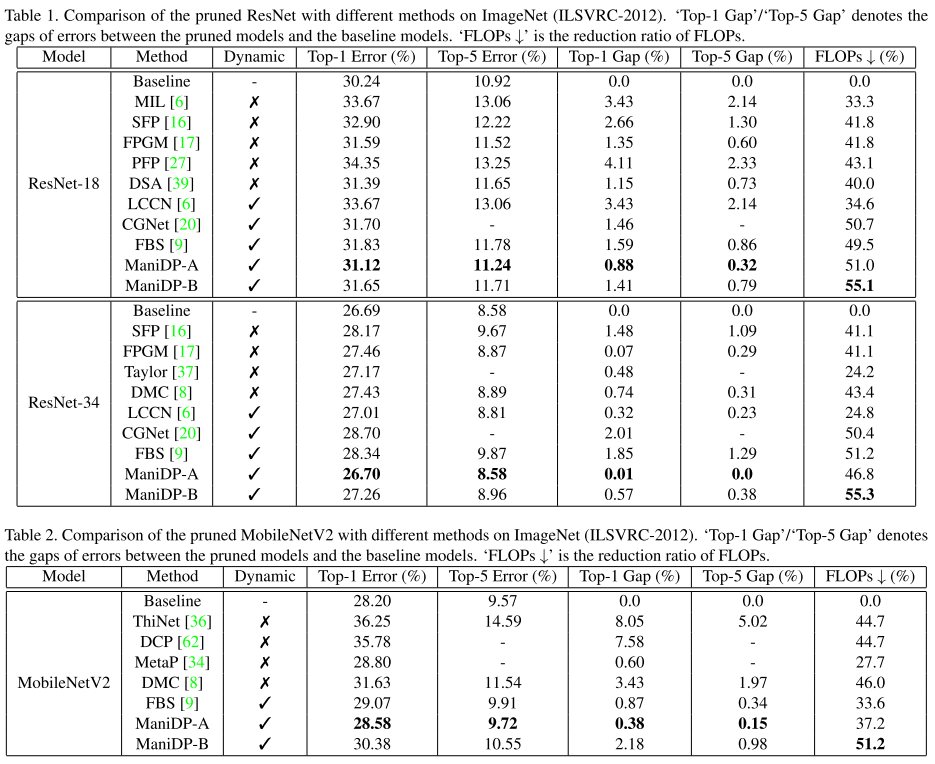
ImageNet
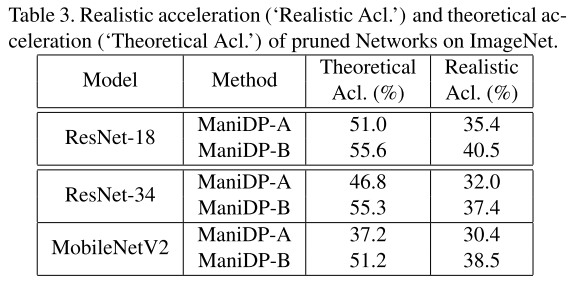
理论加速比（FLOPs）与实际加速比（实际推理时间）
同理，报告的是所有图片的平均实际推理时间
Ablation Study
复杂度/相似度Loss的有效性
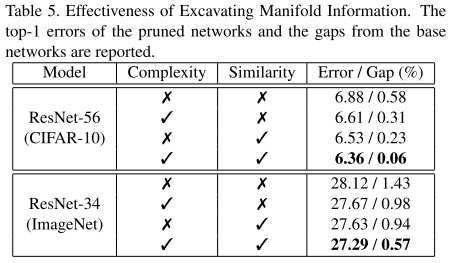
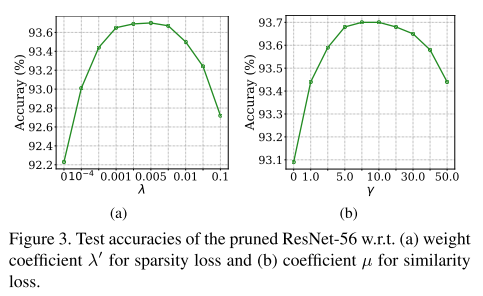
超参 \(\lambda'\) 和 \(\gamma\)
记
总Loss变为：
可视化
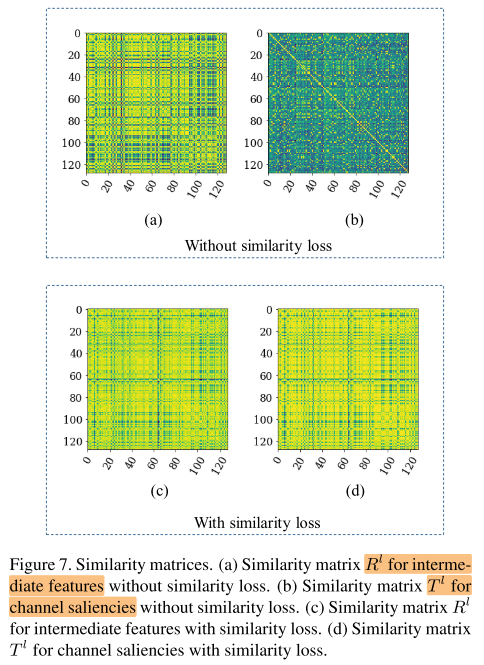
Conclusion
Summary
pros：
- 把动态网络的方法，从动态剪枝的角度来解释
- 用平均 FLOPs 的方式来和静态剪枝方法做对比，在之前动态网络的方法中比较少见
- 逻辑清晰，实验丰富（小数据集，大数据集，实际加速比，模块有效性，超参，可视化）
cons：
- 剪完的模型的加速比（FLOPs）只对当前数据集有参考价值，换个数据集估计加速比就不同了
- 泛化能力，超参的选择（样本复杂度/相似度的学习）结果都十分依赖当前的数据集，换个数据集可能要重新搜索，可能会影响泛化能力
To Read
Reference
https://www.zhihu.com/question/446299297/answer/1755955558
