【WeightNet】2020-ECCV-WeightNet: Revisiting the Design Space of Weight Networks-论文阅读
WeightNet
2020-ECCV-WeightNet: Revisiting the Design Space of Weight Networks
来源:ChenBong 博客园
- Institute:HKUST,MEGVII
- Author:Ningning Ma,Xiangyu Zhang,Jian Sun
- GitHub:https://github.com/megvii-model/WeightNet 100+
- Citation: 3
Prepare
CondConv
条件参数生成
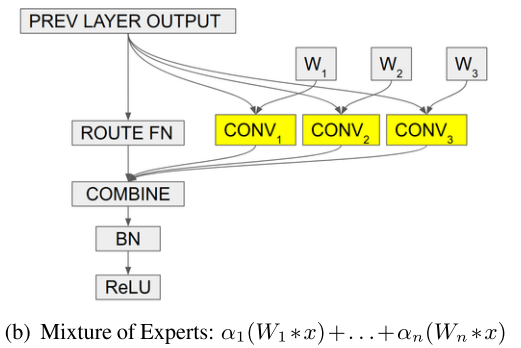
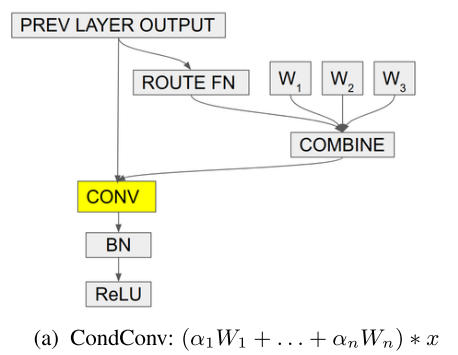
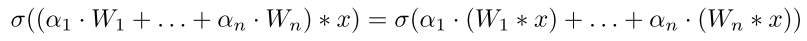
\(\alpha\) 如何得到?
- \(α=r(x)=sigmoid(fc(avg pool(x)))\)
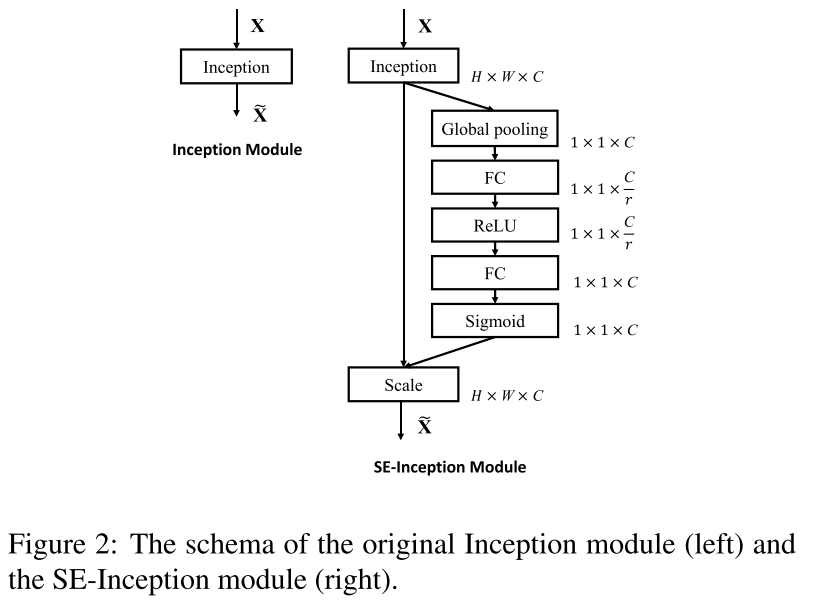
SENet
channel attention 的模块,对卷积层的不同输出通道学习不同的权重 \(α\) :
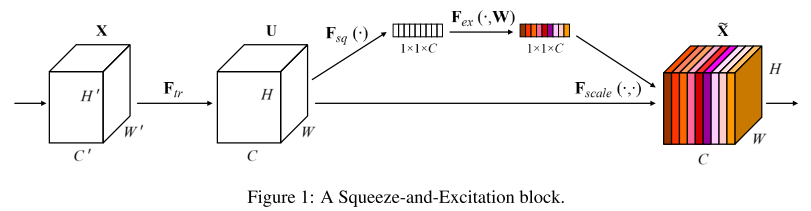
具体细节:GAP ==> FC+relu ==> FC+sigmoid
Introduction
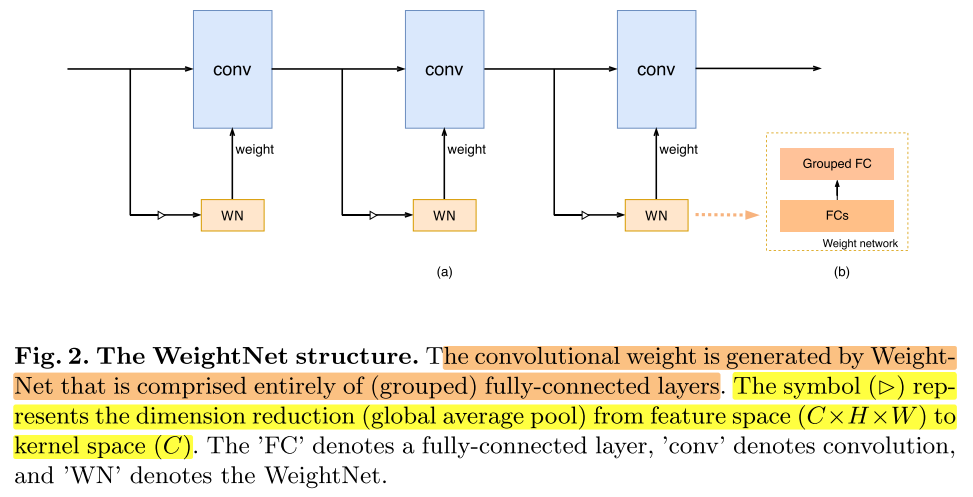
卷积核的参数生成网络,对CondConv和SENet的重新思考,将两种看起来不同的方法统一到一个通用的框架下。
Motivation
Contribution
Method
Group FC

统一两种方法
input feature map: \(X ∈ \mathbb{R}^{C×h×w}\)
output feature map: \(Y ∈ \mathbb{R}^{C×h'×w'}\)
real kernel: \(W' ∈ \mathbb{R}^{C×C×k^h×k^w}\)
\((h,w), (h', w'), (k^h, k^w)\) denote the input, output, and kernel size
第一步:SENet 和 CondConv 的第一步都是使用卷积层的输入x,学习一个attention vector \(α\)
- CondConv
- \(\boldsymbol{\alpha}=\sigma\left(\mathbf{W}_{f c 1} \times \frac{1}{h w} \sum_{i \in h, j \in w} \mathbf{X}_{c, i, j}\right)\)
- 其中,\(W_{fc1} ∈R^{m×c}, X_c∈R^{c×1}\) ,所以 \(\alpha∈R^{m×1}\),m为 expert 的数量
- SENet
- \(\boldsymbol{\alpha}=\sigma\left(\mathbf{W}_{f c_{2}} \times \delta\left(\mathbf{W}_{f c 1} \times \frac{1}{h w} \sum_{i \in h, j \in w} \mathbf{X}_{c, i, j}\right)\right)\)
- 其中 \(\mathbf{W}_{f c 1} \in \mathbb{R}^{C / r \times C}\) \(\mathbf{W}_{f c 2} \in \mathbb{R}^{C \times C / r}\) , \(\mathbf{W}_{f c 2} \in \mathbb{R}^{C \times C / r}\)
第二步:
- CondConv
- \(\mathbf{W}^{\prime}=\alpha_{1} \cdot \mathbf{W}_{1}+\alpha_{2} \cdot \mathbf{W}_{2}+\ldots+\alpha_{m} \cdot \mathbf{W}_{m}\)
- 可以改写为: \(\begin{aligned} \mathbf{W}^{\prime} &=\mathbf{W}^{T} \times \boldsymbol{\alpha} , \text { where } \mathbf{W} =\left[\mathbf{W}_{1} \mathbf{W}_{2} \ldots \mathbf{W}_{m}\right] \end{aligned}\)
- 其中 \(\mathbf{W} \in \mathbb{R}^{m \times C C k_{h} k_{w}}\) , $\alpha \in \mathbb{R}^{m \times 1} $ ,所以 \(\mathbf{W}' \in \mathbb{R}^{C C k_{h} k_{w}}\)
- 可以看成一个全连接层,输入是 \(\alpha\) ,输出新的卷积层权重
- 左边的矩阵为一个稠密矩阵,gruop=1
- SENet
- \(\begin{aligned} \mathbf{Y}_{c} &=\left(\mathbf{W}_{c}^{\prime} * \mathbf{X}\right) \cdot \boldsymbol{\alpha}_{c} \\ &=\left(\mathbf{W}_{c}^{\prime} \cdot \boldsymbol{\alpha}_{c}\right) * \mathbf{X} \end{aligned}\)
- \(\mathbf{W}_c''=\mathbf{W}_{c}^{\prime} \cdot \boldsymbol{\alpha}_{c}\)
- 其中,\(\mathbf{W}_{c}' \in \mathbb{R}^{C \times C \times k_h \times k_w},\ \alpha \in \mathbb{R}^{C \times 1}\)
- 可以看成一个分组全连接层,gruop=C, 输入是 \(\alpha\) ,输出新的卷积层权重
- 左边的矩阵为一个稀疏矩阵,gruop=C
两种方法都可以看成是先使用 input 计算α,再利用α计算当前卷积核的实际推理权重
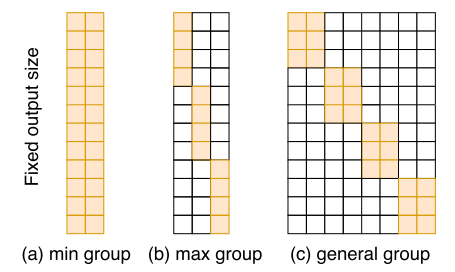
(a) CondConv
- input: m
- output:\(C ×C × k_h × k_w\)
- gruop:1
(b) SENet
- input: \(C\)
- output:\(C ×C × k_h × k_w\)
- gruop:C
(c) WeightNet
- input:\(M × C\)
- output:\(C ×C × k_h × k_w\)
- gruop:\(G×C\)
引入M和G,2个超参数

WeightNet
第一步:计算attention vector α
- \(\boldsymbol{\alpha}=\sigma\left(\mathbf{W}_{f c_{2}} \times \mathbf{W}_{f c 1} \times \frac{1}{h w} \sum_{i \in h, j \in w} \mathbf{X}_{c, i, j}\right)\)
- 其中, \(\mathbf{W}_{f c 1} \in \mathbb{R}^{C / r \times C}, \mathbf{W}_{f c 2} \in \mathbb{R}^{M C \times C / r}\) ,r取16
第二步:gruop fc layer,输入α,输出当前卷积层的实际推理权重
- input:\(M × C\)
- output:\(C ×C × k_h × k_w\)
- gruop:\(G×C\)
将实际卷积核的参数 实际上可以看成存储在第二步中分组全连接层的参数当中
复杂度
计算复杂度
每一层的实际推理有2个步骤,1)权重生成,2)卷积计算
1)权重生成:\(O(MCCk_hk_w/G)\) ,和2比起来很小,可以忽略
2)卷积计算:\(O(hwCCk_hk_w)\)
参数复杂度
1)权重生成:\(O(M/G×C×C×k_h×k_w)\) ,这里应该忽略了第一步中计算α的2个fc的参数
2)卷积计算:0
将 \(M/G\) 记为 \(λ\) (参数倍数)
Experiments
ImageNet
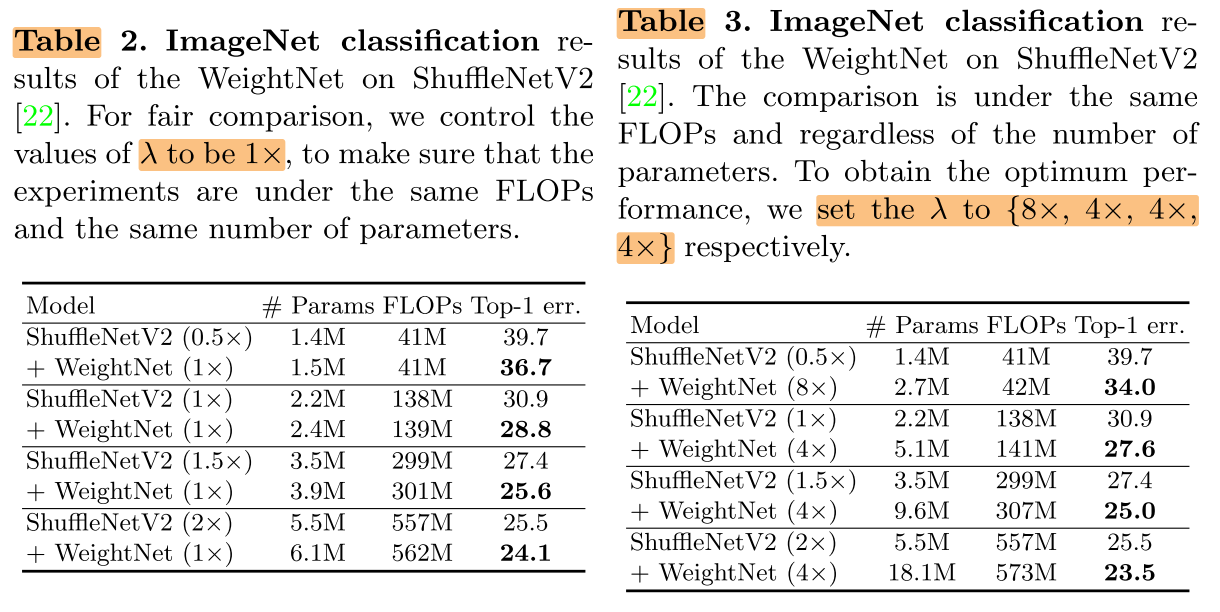
G=2,λ=1/2/4/8
在计算量不变的情况下,提升模型性能,模型越小提升效果越明显
attention modules
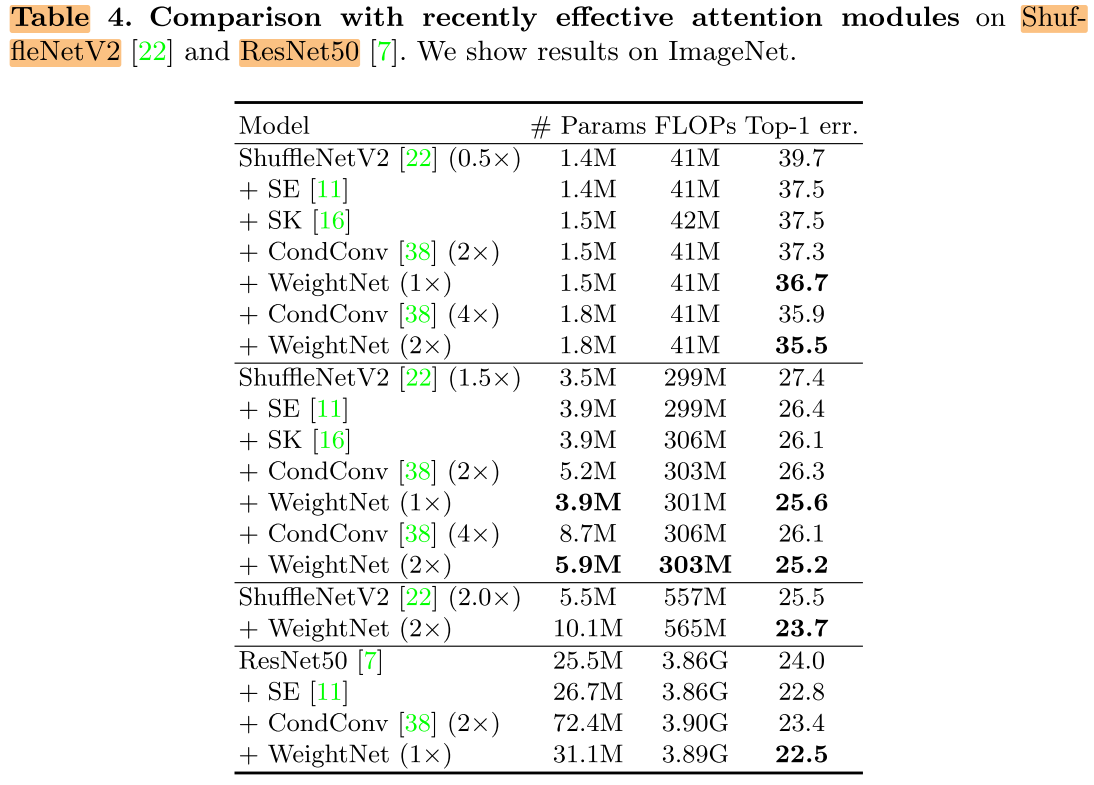
小网络上,CondConv性能更好
Ablation
λ

λ越大,模型参数量越大
G
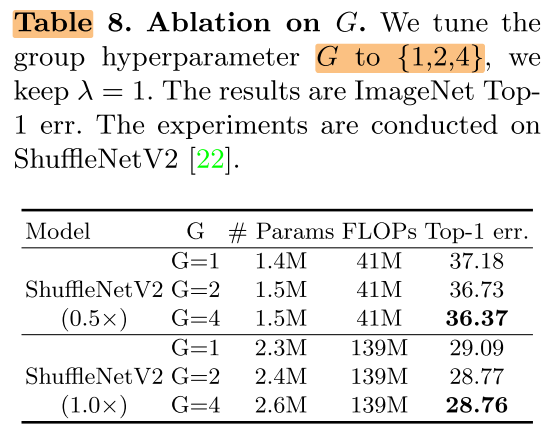
分组数G越大,性能越好
kernel相似性
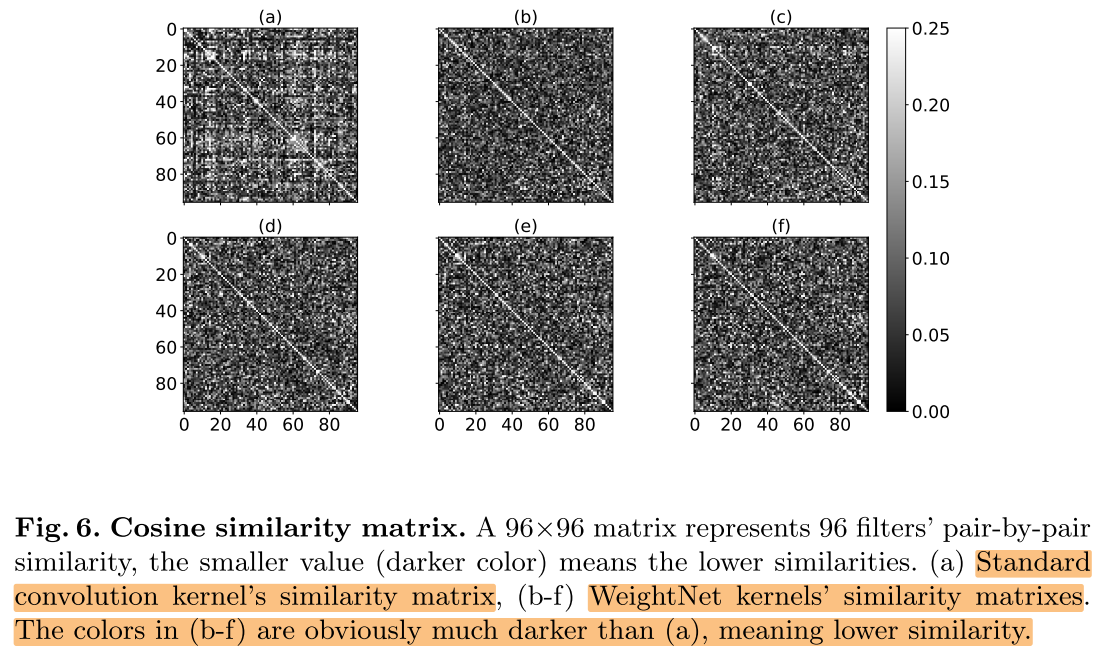
本文的方法生成的卷积核的kernel之间的相似性更低
Conclusion
Summary
To Read
Reference
SENet:
https://zhuanlan.zhihu.com/p/32702350
https://www.cnblogs.com/bonelee/p/9030092.html
WeightNet:
https://mp.weixin.qq.com/s/uI1oEXqlqeyJ4NfyT0f40Q
https://mp.weixin.qq.com/s/EhdrYfM25xGiVKWXhh8reQ

