【PENNI】2020-ICML-PENNI: Pruned Kernel Sharing for Efficient CNN Inference-论文阅读
PENNI
2020-ICML-PENNI: Pruned Kernel Sharing for Efficient CNN Inference
来源：ChenBong 博客园
- Institute：Duke University
- Author：Shiyu Li、Yiran Chen
- GitHub：https://github.com/timlee0212/PENNI
- Citation：/
Introduction
kernel granularity decomposition
weight sparsity ==> channel sparsity
Method
Notion
layer \(l\) weight： \(θ^{(l)}\)
Network weight: \(\Theta=\{θ^{(l)}\}\)
layer l input feature map: \(I^{l-1}\)
layer l output feature map: \(S^{l}\)
\(S_{i}^{(l)}=\sigma^{(l)}\left(\left(\sum_{j=1}^{c_{l-1}} I_{j}^{(l-1)} * \theta_{i, j}^{(l)}\right)+b_{j}^{(l)}\right)\)
Decomposition
\(θ^{(l)}∈R^{c_l×c_{l+1}×k×k}\)
reshape： \(θ'^{(l)}∈R^{c_lc_{l+1}×k^2}\)
each kernel \(w\) can be seen as its row vertor: \(w∈R^{k^2}\)
\(R^{k^2}\) 的一个子空间 \(R^{d}, d<d^2\)
将 \(θ'^{(l)}∈R^{c_lc_{l+1}×k^2}\) 近似为矩阵 \(B∈R^{k^2×d}\)
分解过程的目标是最小化 近似矩阵B 与原始 权重矩阵的误差：
\(\min _{\alpha_{w} \in \mathbb{R}^{d}} \sum_{w \in \theta^{\prime}}\left\|w-\alpha_{w} \mathbf{B}^{T}\right\|^{2}\)
其中 \(α_ω\) 为投影向量
Retraining
虽然近似矩阵已经尽量逼近原始 权重矩阵 θ，但依然会有很大的精度损失，
重训练过程，θ 替换为 \(αB^T\)
\(S_{i}^{(l)}=\sigma^{(l)}\left(\left(\sum_{j=1}^{c_{l-1}} I_{j}^{(l-1)} *\left(\alpha_{i, j}^{(l)} \mathbf{B}^{(l) T}\right)+b_{j}^{(l)}\right)\right.\)
损失函数：
\(\mathcal{L}^{\prime}=\mathcal{L}(\Theta, X, Y)+\gamma \sum_{l} \sum_{i}^{c_{l} c_{l+1}}\left\|\alpha_{i}^{(l)}\right\|_{1}\)
第一项是原始loss， 第二项作用是使得投影向量稀疏化
如果联合训练B和α，则α会在原来的B上进行更新，这会导致模型难以收敛。为此，作者采取了交替训练的方式：冻结α，训练B；然后冻结B训练α。
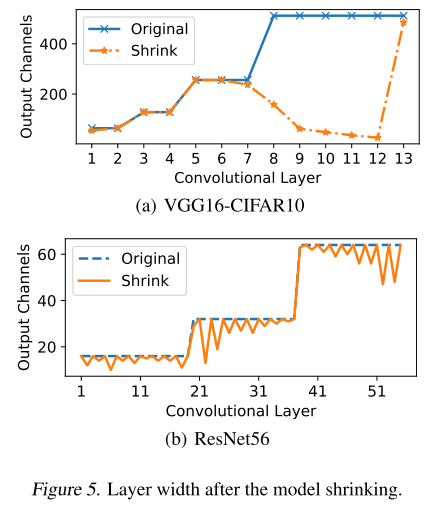
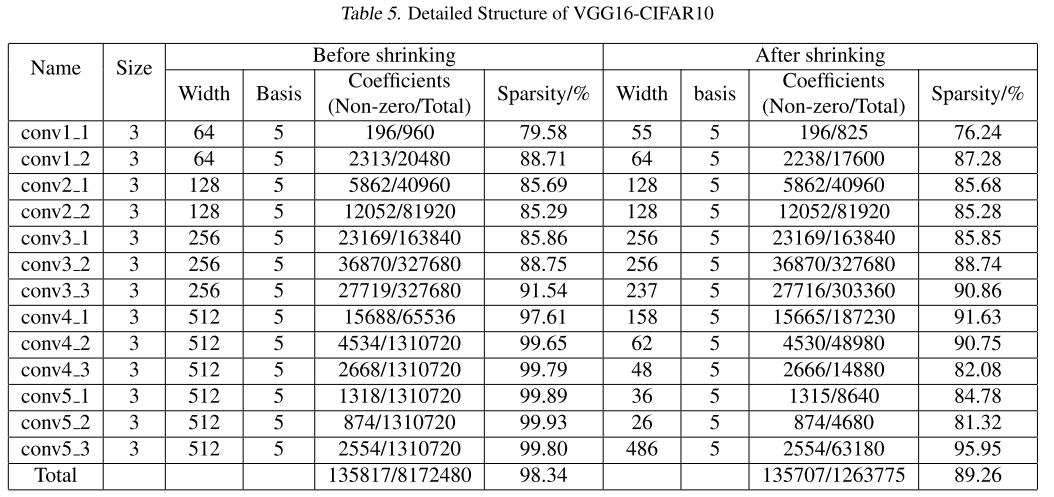
Model Shrinking/Pruning
经过上一步的 Retraining，会使得重构权重稀疏化，
将重构权重矩阵 reshape 为 \(c_{l} \times c_{l+1} \times k^{2}\)
对重构矩阵 保持 \(c_{in}\) 维度的基础上 sum，得到一维向量 \(p_i\) ，其中低于阈值的输入通道置零
对重构矩阵 保持 \(c_{out}\) 维度的基础上 sum，得到一维向量 \(p_o\) ，其中低于阈值的输出通道置零
输入/输出通道不对齐，取交集：
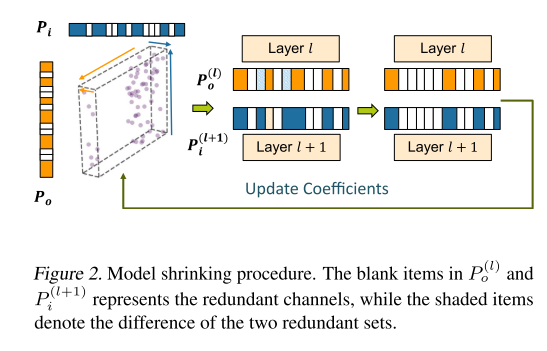
完成 filter 剪枝
Experiments
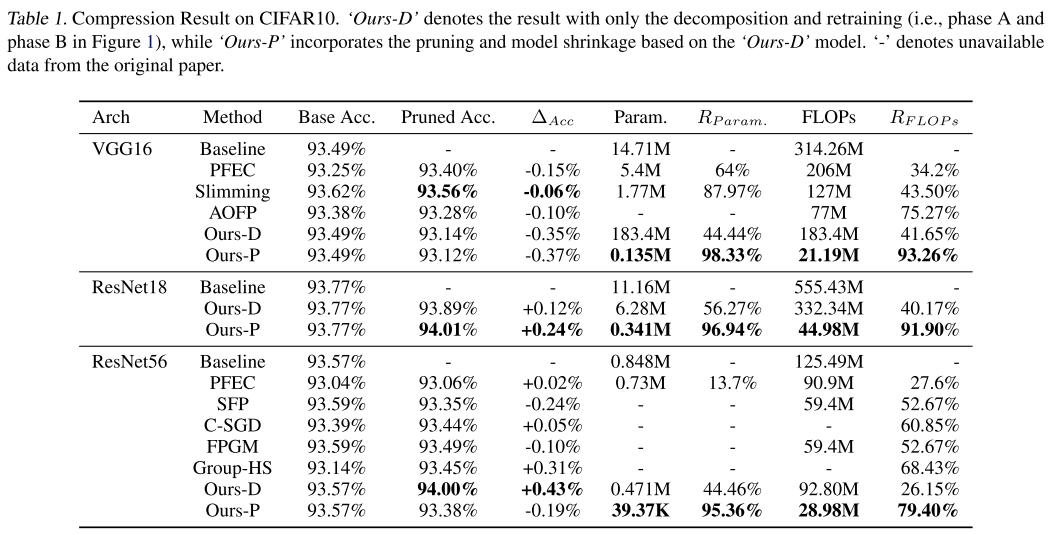
CIFAR-10
D-只分解
P-分解+剪枝
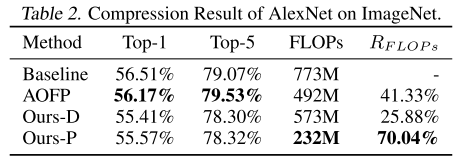
ImageNet
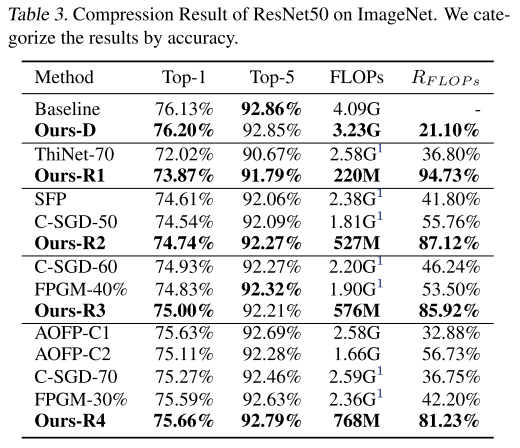
Visualization
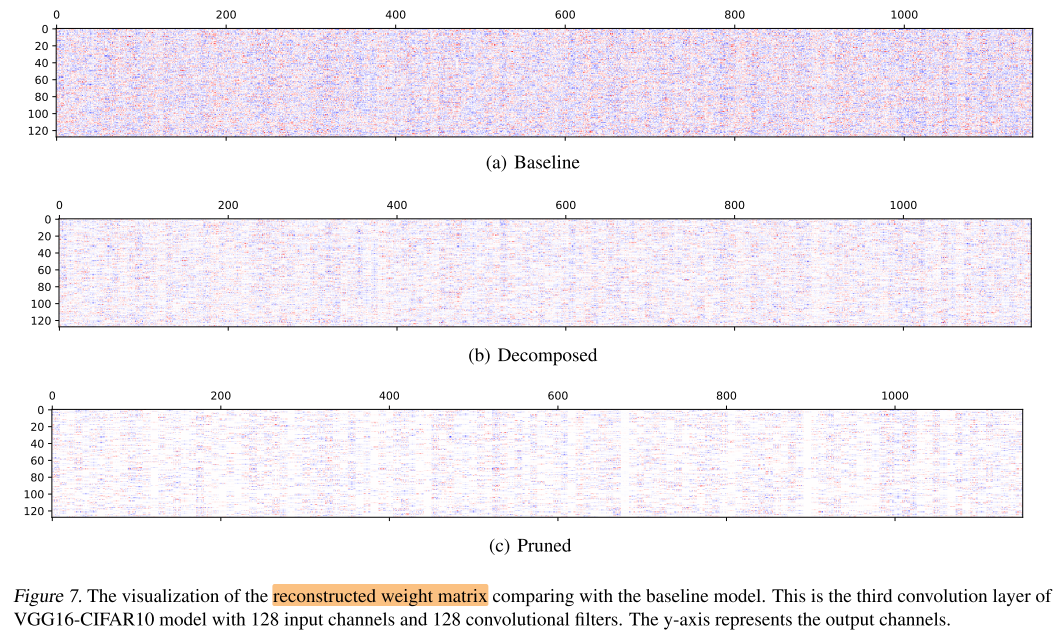
Conclusion
Summary
权重稀疏 到 结构化稀疏 的转化
