Loading

【DARTS】2019-ICLR-DARTS: Differentiable Architecture Search-论文阅读

DARTS

2019-ICLR-DARTS Differentiable Architecture Search

来源：ChenBong 博客园


问题

&& 更新结构参数α时, 有用到指数移动平均EMA吗?

没有


&& op的padding操作, 是先padding再卷积, 还是先卷积再padding?

先padding再卷积


&& FactorizedReduce() 函数的作用?

将feature map缩小为原来的一半


&& Reduction Cell的哪个Node的Stride=2? Reduction Cell中Node的具体输入输出?

不是reduction cell中的node 的stride=2，而是reduction cell的预处理的stride=2，具体见离散网络结构 部分


&& Cell_3 Node_0 的size预处理是什么?

# 如果[k-1] cell 是reduction cell, 当前cell的input size=[k-1] cell 的 output size, 因此不匹配[k-2] cell 的 output size
# 因此[k-2] cell 的output需要 reduce 处理
if reduction_p:
 # 如果[k-1] cell 是reduction cell: 将feature map缩小为原来的一半
 # input node_0: 处理[k-2]cell的output
 self.preproc0 = ops.FactorizedReduce(channels_pp, channels, affine=False)
 else:
     # 如果[k-1] cell 不是reduction cell: 标准1x1卷积
     # input node_0: 处理[k-2]cell的output
     self.preproc0 = ops.StdConv(channels_pp, channels, 1, 1, 0, affine=False)

&& α/w的更新, 是以batch为单位还是epochs为单位?

以batch为单位


&& 更新α用的优化器是什么? 具体参数? 具体操作?

self.ctrl_optim = torch.optim.Adam(self.mutator.parameters(), arc_learning_rate, 
                                   betas=(0.5, 0.999),weight_decay=1.0E-3)

&& 实际上权重的更新时怎么做的? 只更新一步吗?

一阶近似时，更新一次；

二阶近似时，


&& 用val set 更新α, 用train set 更新w, 数据集划分?

val set 为 cifar10 的 test set


Introduction


Motivation

之前的NAS方法：

  • 高昂的计算代价：2000/3000 GPU days
  • 离散的搜索空间，导致大量的结构需要评估

Contribution

  • 基于梯度下降的可微分方法
  • 可以用在CNN和RNN上
  • 在CIFAR-10和PTB数据集上达到SOTA
  • 高效性：2000 GPU days vs 4 GPU days
  • 可迁移性：在cifar10上搜索的结构迁移到ImageNet上，在PTB上搜索的结构迁移到WikiText-2上

Method

搜索空间

搜索cell结构作为最终网络结构的构建块（building block）

搜素到的cell可以堆叠构成CNN或者RNN

一个cell是一个包含N个节点的有向无环图（DAG）

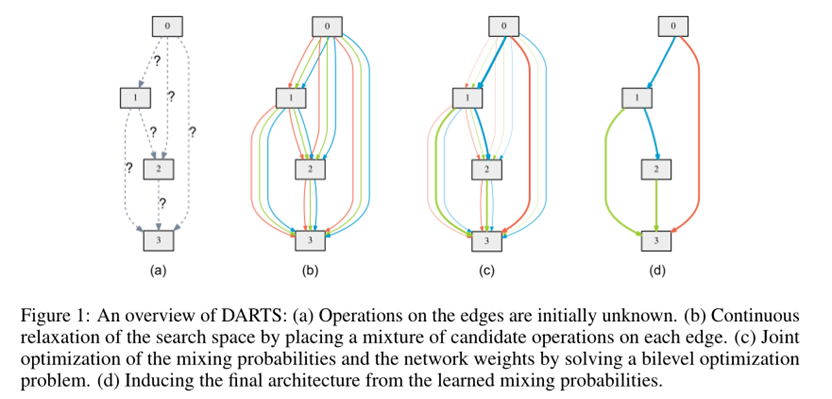
image-20200524185550276

图1说明：

图1表示一个cell结构；每个节点都会连接到比自身编号小的节点上；

节点 i 表示feature maps（\(x^{(i)}\)），节点之间不同颜色的箭头表示不同op，每个op都有自己的权重；

节点之间的操作选自op集O, 两个节点之间的op数=|O|;

节点 i, j 之间的每个op都对应一个结构参数（\(α^{(i, j)}\)）(可以理解为该op的强度/权重等)，\(α^{(i,j)}\) 是一个|O|维的向量;

\(x^{(j)}=\sum_{i<j} o^{(i, j)}\left(x^{(i)}\right) \qquad (1)\)

公式（1）说明：

  • \(x^{(i)}\) 表示第i个节点的feature map
  • \(o^{(i, j)}\) 是一组op集合
  • \(o^{(i, j)}\left(x^{(i)}\right)\) 表示对feature map \(x^{(i)}\) 执行op集 \(o^{(i, j)}\) 得到新的feature map
  • 对所有小于j的节点i，都执行 \(o^{(i, j)}\left(x^{(i)}\right)\) ，并将结果求和，得到 j 节点的feature map

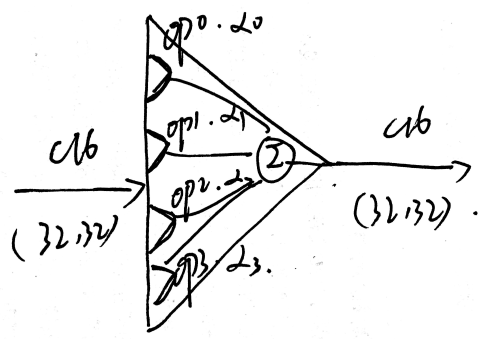
\(\bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x) \qquad (2)\)

公式（2）说明：

  • 向量 \(α^{ij}\) 的维度是|O|
  • 对 \(α^{(i, j)}\) 执行softmax，得到softmax后的结构参数 \(\hat{α}^{(i, j)}=\frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)}\)
  • 将op集合O中的每个op都施加在x上，并乘以对应的结构参数 \(\hat{α}^{(i, j)}\) ，再求和，得到 \(\bar{o}^{(i, j)}(x)\)
  • 则mix op 记为 \(\bar{o}^{(i, j)}(·)\)

&& 两个node之间, 不同颜色的op的output feature map size 不一样怎么办?

两个node之间, input size相同, 由于op类型不同, 会导致不同op输出的output size不同, 代码中是通过padding来保持不同op的output feature map维度统一的

image-20200807222744639


&& 两个node之间, 不同颜色的op的output feature maps 是如何整合的? 求和还是concat?

不同op的的output feature maps (通道数和size都相同) 会进行求和 (对应位置元素相加), 因此多个op的output feature maps 整合后, feature map的通道数和size都不变


&& 来自不同node的 output feature maps 如何整合？求和还是concat？

求和


\(o^{(i, j)}=\operatorname{argmax}_{o \in \mathcal{O}} \alpha_{o}^{(i, j)}\)

公式说明：

在搜索的最后阶段三条不同颜色的线会保留对应结构参数 \(α^{(i, j)}\) 最大的那一条

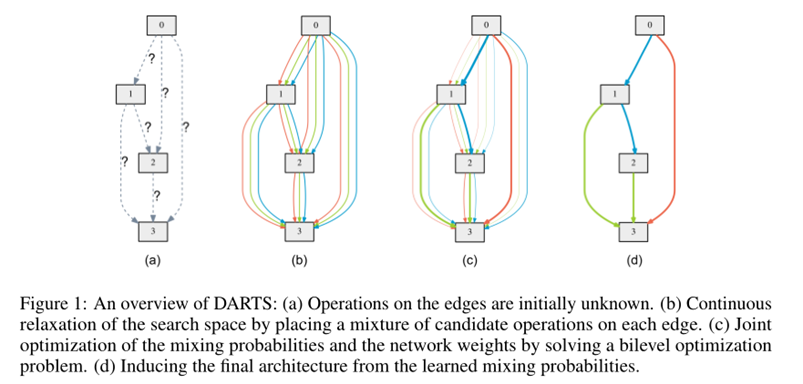
image-20200524185838715


结构图例说明

**CNN cell结构: **

image-20200808160326838

其中每个三角形代表图1中两个node之间的一组操作, 即每个三角形表示公式(2)的操作: \(\bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x) \qquad (2)\) , 到最后, 图1中的每组线会只保留一个op, 即每个三角形到最后也只保留1个强度最大的op. 而且每个node会选择n个op中强度最大的2个.

image-20200808160542699

最后每个三角形(对应图1中两个node之间的一组操作)

CNN结构:

666

一个三角形表示图1中两个node之间的一组op:

\(\bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x) \qquad (2)\)

image-20200808160542699

优化目标

我们的目标是联合学习结构参数（α）和网络权重（w）：

\(\min _{\alpha} \mathcal{L}_{v a l}\left(w^{*}(\alpha), \alpha\right) \qquad (3)\)

s.t. \(\quad w^{*}(\alpha)=\operatorname{argmin}_{w} \mathcal{L}_{\text {train}}(w, \alpha) \qquad (4)\)

公式（3）（4）说明：

  • \(w^{*}(\alpha)\) 是结构参数取值为 \(α\) 时最佳的网络权重，即不同的 \(α\) 对应不同的最佳网络权重 \(w^{*}(\alpha)\)
  • 训练流程：
    • 每次改变 \(α\) ，先将网络权重训练到对应的最佳网络权重 \(w^{*}(\alpha)\) ，——公式（4）
    • 对结构参数 \(α\) 梯度下降，尝试不同的结构参数 \(α\) ，找到使得loss最小的结构参数 \(α\)，即找到了最佳的结构——公式（3）

image-20200524185951756

算法（1）DARTS-可微分的结构搜索 说明：

  • 根据结构参数 \(α^{(i, j)}\) 构建mix op \(\bar{o}^{(i, j)}(·)\)
  • 若（还未收敛），执行：
    • 梯度下降更新结构参数 \(α\) ： \(\nabla_{\alpha} \mathcal{L}_{v a l}\left(w-\xi \nabla_{w} \mathcal{L}_{t r a i n}(w, \alpha), \alpha\right)\)
    • 梯度下降更新网络权重 w： \(\nabla_{w} \mathcal{L}_{t r a i n}(w, \alpha)\)
  • 根据收敛后的 \(α\) 导出最终结构

近似处理

每次更新 \(α\) 后，如果重新训练网络权重到收敛，需要消耗大量时间，我们希望通过简化公式（3），只更新一次，来近似逼近 \(w^{*}(\alpha)\) ，而不是通过训练到收敛来获得 \(w^{*}(\alpha)\)

\(\nabla_{\alpha} \mathcal{L}_{v a l}\left(w^{*}(\alpha), \alpha\right) \qquad (5)\)

\((5)\approx \nabla_{\alpha} \mathcal{L}_{v a l}\left(w-\xi \nabla_{w} \mathcal{L}_{t r a i n}(w, \alpha), \alpha\right) \qquad(6)\)

公式(6) 说明:

\(\xi\) 是一个超参, 代表权重一步优化的学习率, 在结构参数 \(α\) 更新后, 该公式通过只更新一步网络权重(本来要更新到收敛), 来近似收敛后的网络权重. 注意到如果w已经是最优时, 即 \(\nabla_{w} \mathcal{L}_{\text {train}}(w, \alpha)=0\) 时, (6)将退化为 \(\nabla_{\alpha} \mathcal{L}_{v a l}(w, \alpha)\)


\((6)=\nabla_{\alpha} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right)-\xi \nabla_{\alpha, w}^{2} \mathcal{L}_{t r a i n}(w, \alpha) \nabla_{w^{\prime}} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right) \qquad (7)\)

(7)式中的 \(w^{\prime}=w-\xi \nabla_{w} L_{t r a i n}(w, \alpha)\)

公式(7)说明:

式(6)应用链式法则, 可得式(7)

&& (7)式后面包含了一个计算复杂度很高的矩阵乘法 $\xi \nabla_{\alpha, w}^{2} \mathcal{L}{t r a i n}(w, \alpha) \nabla{w^{\prime}} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right) $ ，文中提出有限差分近似的方法解决, 如下.


设 \(w^{\pm}=w \pm \epsilon \nabla_{w^{\prime}} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right)\) 则:

\(\nabla_{\alpha, w}^{2} \mathcal{L}_{t r a i n}(w, \alpha) \nabla_{w^{\prime}} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right) \approx \frac{\nabla_{\alpha} \mathcal{L}_{t r a i n}\left(w^{+}, \alpha\right)-\nabla_{\alpha} \mathcal{L}_{t r a i n}\left(w^{-}, \alpha\right)}{2 \epsilon} \qquad (8)\)

公式(8)说明:

&& 评估该 有限差分 仅需要两次前向传播即可得到 weights，两次反向传播，就可以得到 α，运算复杂度大大的降低了： \(O(|\alpha||w|)\) to \(O(|\alpha|+|w|)\)

理论上 \(\epsilon\) 要足够小, 经验上取 \(\epsilon=0.01 /\left\|\nabla_{w^{\prime}} \mathcal{L}_{v a l}\left(w^{\prime}, \alpha\right)\right\|_{2}\) 即可足够精确.


\(\xi\) 取值讨论:

  • 当 \(\xi = 0\) , 式(7)中的二阶导数将消失, 因此
    • 设 \(\xi = 0\) , 此时为一阶近似
    • 设 \(\xi > 0\) , 此时为二阶近似, 这种情况下, 简单的策略是将 \(\xi\) 设置为网络权重w的学习率

\(\xi\) 取值实验:

设置简单的损失函数:

  • \(\mathcal{L}_{\text {val}}(w, \alpha)=\alpha w-2 \alpha+1\)
  • \(\mathcal{L}_{\text {train}}(w, \alpha)=w^2-2\alpha w+ \alpha^2\)

\(\xi\) 取不同的值, 优化过程如下图:

image-20200524190209578

image-20200524190443350


连续结构=>离散结构

为了构造离散的结构的cell中的每个节点（即边上不存在结构参数 或者说 结构参数均为1），对于每个节点，我们都保留op强度最强的k个边，对于CNN来说k=2，对于RNN来说k=1。

即下图中，CNN cell 的每个node 都有k=2个输入，RNN cell 的每个node 都有k=1个输入。

&& 代码中如何实现？

&& 堆叠cell以后, 多个cell是否是相同的? 如何实现?

op强度定义为： \(\frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)}\)

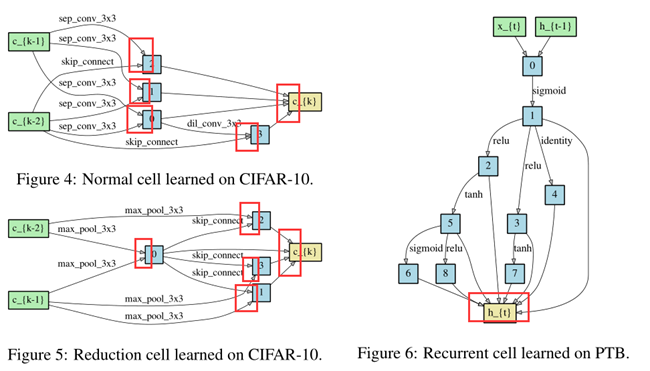
image-20200524190637100


Experiments

以下是op集 O 中的op：

  • 3 × 3 and 5 × 5 separable convolutions,
  • 3 × 3 and 5 × 5 dilated separable convolutions,
  • 3 × 3 max pooling,
  • 3 × 3 average pooling,
  • identity (skip connection?)
  • zero.

所有的op：

  • stride = 1（如有需要的话）
  • 不同操作的feature map（分辨率可能不同）都进行pad以保持相同的分辨率

我们使用：

  • 对于卷积操作，使用 ReLU-Conv-BN的顺序
  • 每个可分离卷积都应用两次
  • CNN cell包含N=7个Nodes，output node定义为所有中间节点（feature maps）的concat

&& concat维度不同如何处理？

image-20200524190900372

每个cell包含2个input node，和1个output node

  • 第k个cell 的 2个input node 分别等于 第k-2个cell 和 第 k-1 个cell的output node
  • 位于网络深度 1/3 和 2/3 的2个cell，设置为reduction cell，即cell中的op 的stride=2
  • 因此有2种不用的cell，分别称为Normal cell 和 Reduce cell，两种cell的结构参数不同，分别称为 \(α_{normal}, α_{reduce}\)
  • 其中 \(α_{normal}\) 在所有 Normal cell 中共享，\(α_{reduce}\) 在所有 Reduce cell 中共享

  • 为了确定最终的结构，我们用不同的 random seeds运行DARTS 4次，并将4次的结果train from scratch 少量epochs（100 epochs for CIFAR-10，300 epochs for PTB），根据训练少量epochs后的性能来挑选最佳cell
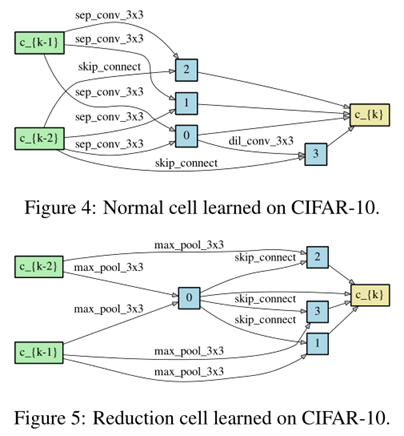
  • 由于cell要进行多次堆叠，因此运行多次搜索是必要的，而且结果可能是初始值敏感的，如下图2,4：

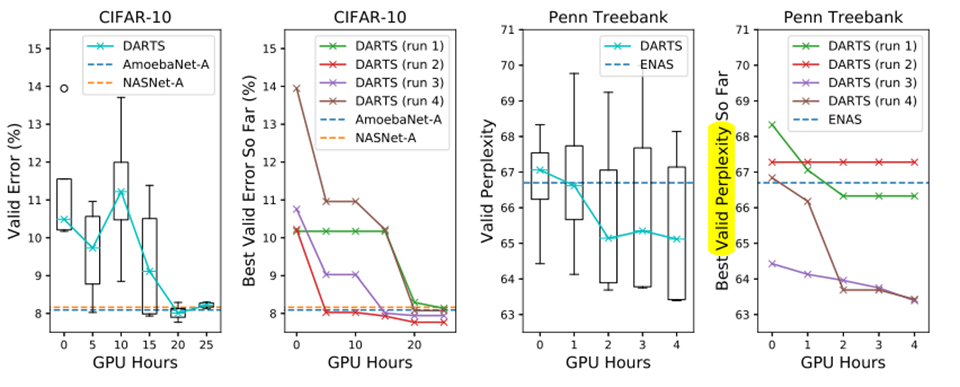
image-20200524191124715


结构评估

为了评估搜索到的结构，我们随机初始化结构的权重（在搜索过程中学习的权重被抛弃），train from scratch，并报告了其在测试集上的权重。


image-20200524191204869


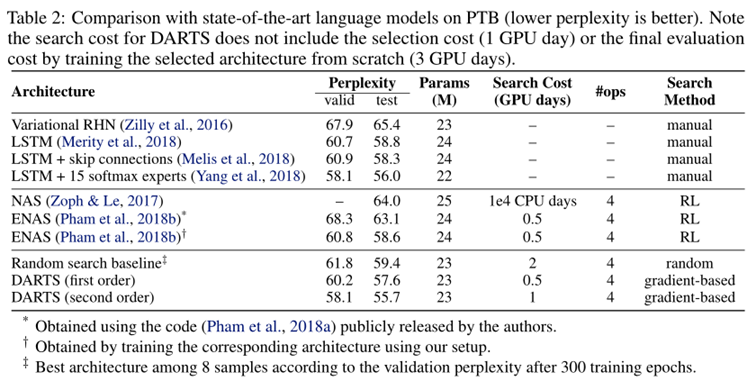
image-20200524191223691


结果分析

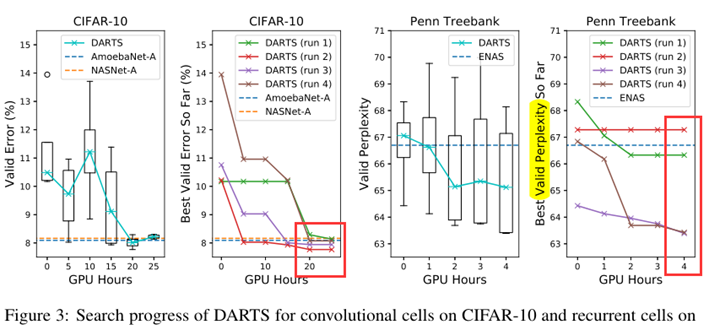
image-20200524191305687

图3说明:

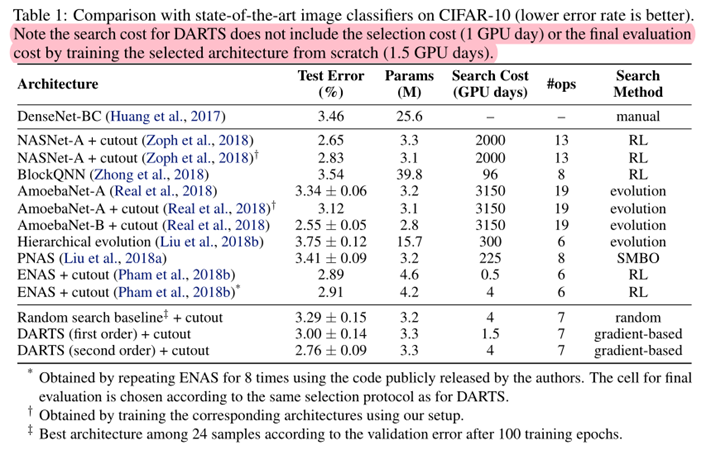
  • DARTS在减少3个数量级的计算量的基础上达到了与SOTA相当的结果
    • (i.e. 1.5 or 4 GPU days vs 2000 GPU days for NASNet and 3150 GPU days for AmoebaNet)
  • 较长的搜索时间是由于我们对cell 的选择重复搜索了4次，这种做法对CNN cell 来说不是特别重要，CNN cell 的初值敏感性较不明显，RNN cell 的初值敏感性较大

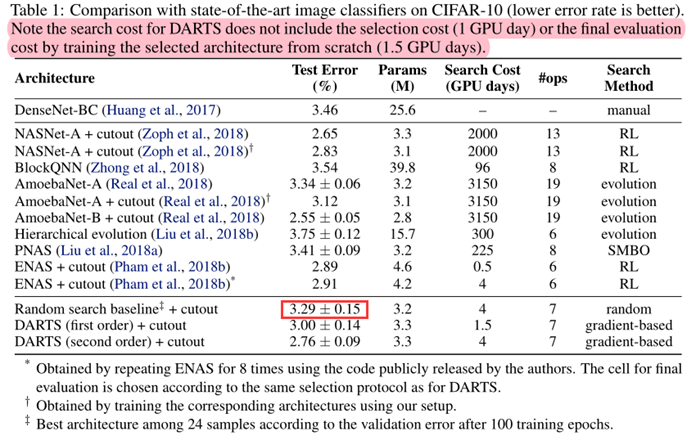
image-20200524191326038

表1说明：

  • 从表1可以看出，随机搜索的结果也具有竞争力，说明本方法搜索空间设计的较好。

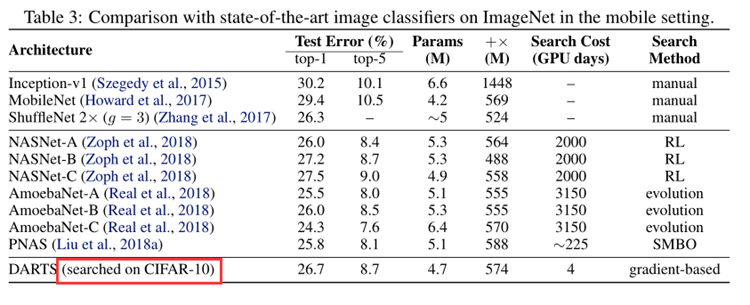
image-20200524191354234

表3说明：

  • 在cifar10上搜索的cell，确实可以被迁移到ImageNet上。

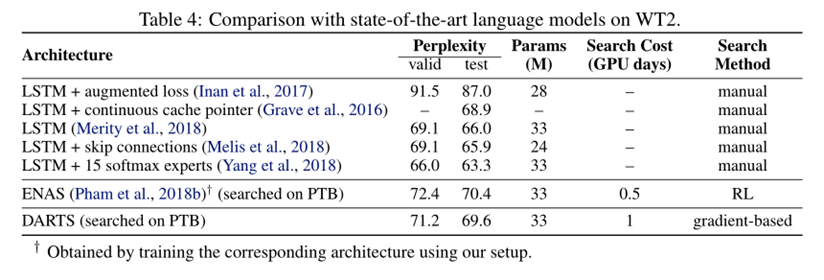
image-20200524191620480

表4说明：

  • 表4中可看出，PTB与WT2之间的可迁移性较弱（与CIFAR-10和ImageNet的可迁移性相比），原因是用于搜索结构的源数据集（PTB）规模较小
  • 可以直接对感兴趣的数据集进行结构搜索，可以避免迁移性的问题

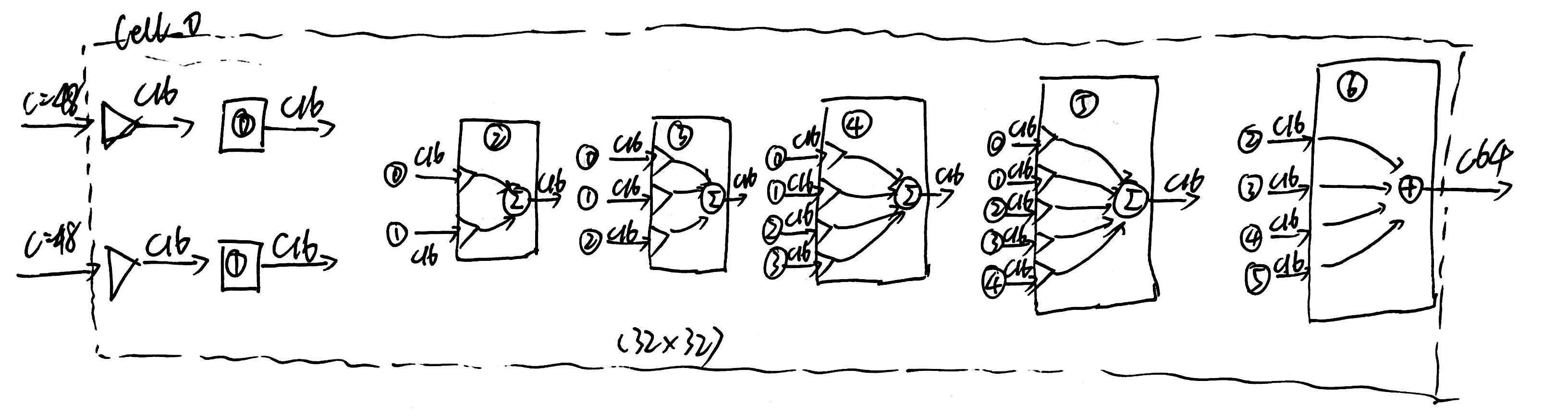
搜索过程中网络输入输出的变化

CNN:==================================================================
CNN In:  torch.Size([32, 3, 32, 32])
CNN stem In : torch.Size([32, 3, 32, 32])
CNN stem Out: torch.Size([32, 48, 32, 32]), torch.Size([32, 48, 32, 32])

Cell_0:========================
Cell_0 In:  torch.Size([32, 48, 32, 32]) torch.Size([32, 48, 32, 32])

Preproc0_in:  torch.Size([32, 48, 32, 32]), Preproc1_in: torch.Size([32, 48, 32, 32])
Preproc0_out: torch.Size([32, 16, 32, 32]), Preproc1_out: torch.Size([32, 16, 32, 32])

  Node_0 In:    1 x torch.Size([32, 16, 32, 32])
  Node_0 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_1 In:    1 x torch.Size([32, 16, 32, 32])
  Node_1 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_2 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_2 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_3 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_3 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_4 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_4 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_5 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_5 Out:   1 x torch.Size([32, 16, 32, 32])

Cell_0 Out: torch.Size([32, 64, 32, 32])

Cell_1:========================
Cell_1 In:  torch.Size([32, 48, 32, 32]) torch.Size([32, 64, 32, 32])

Preproc0_in:  torch.Size([32, 48, 32, 32]), Preproc1_in: torch.Size([32, 64, 32, 32])
Preproc0_out: torch.Size([32, 16, 32, 32]), Preproc1_out: torch.Size([32, 16, 32, 32])

  Node_0 In:    1 x torch.Size([32, 16, 32, 32])
  Node_0 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_1 In:    1 x torch.Size([32, 16, 32, 32])
  Node_1 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_2 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_2 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_3 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_3 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_4 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_4 Out:   1 x torch.Size([32, 16, 32, 32])

  Node_5 In:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node pre_Out:
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
     torch.Size([32, 16, 32, 32])
  Node_5 Out:   1 x torch.Size([32, 16, 32, 32])

Cell_1 Out: torch.Size([32, 64, 32, 32])

Cell_2:========================
Cell_2 In:  torch.Size([32, 64, 32, 32]) torch.Size([32, 64, 32, 32])

Preproc0_in:  torch.Size([32, 64, 32, 32]), Preproc1_in: torch.Size([32, 64, 32, 32])
Preproc0_out: torch.Size([32, 32, 32, 32]), Preproc1_out: torch.Size([32, 32, 32, 32])

  Node_0 In:    1 x torch.Size([32, 32, 32, 32])
  Node_0 Out:   1 x torch.Size([32, 32, 32, 32])

  Node_1 In:    1 x torch.Size([32, 32, 32, 32])
  Node_1 Out:   1 x torch.Size([32, 32, 32, 32])

  Node_2 In:
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 32, 32])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_2 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_3 In:
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_3 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_4 In:
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_4 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_5 In:
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 32, 32])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_5 Out:   1 x torch.Size([32, 32, 16, 16])

Cell_2 Out: torch.Size([32, 128, 16, 16])

Cell_3:========================
Cell_3 In:  torch.Size([32, 64, 32, 32]) torch.Size([32, 128, 16, 16])

Preproc0_in:  torch.Size([32, 64, 32, 32]), Preproc1_in: torch.Size([32, 128, 16, 16])
Preproc0_out: torch.Size([32, 32, 16, 16]), Preproc1_out: torch.Size([32, 32, 16, 16])

  Node_0 In:    1 x torch.Size([32, 32, 16, 16])
  Node_0 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_1 In:    1 x torch.Size([32, 32, 16, 16])
  Node_1 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_2 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_2 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_3 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_3 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_4 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_4 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_5 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_5 Out:   1 x torch.Size([32, 32, 16, 16])

Cell_3 Out: torch.Size([32, 128, 16, 16])

Cell_4:========================
Cell_4 In:  torch.Size([32, 128, 16, 16]) torch.Size([32, 128, 16, 16])

Preproc0_in:  torch.Size([32, 128, 16, 16]), Preproc1_in: torch.Size([32, 128, 16, 16])
Preproc0_out: torch.Size([32, 32, 16, 16]), Preproc1_out: torch.Size([32, 32, 16, 16])

  Node_0 In:    1 x torch.Size([32, 32, 16, 16])
  Node_0 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_1 In:    1 x torch.Size([32, 32, 16, 16])
  Node_1 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_2 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_2 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_3 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_3 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_4 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_4 Out:   1 x torch.Size([32, 32, 16, 16])

  Node_5 In:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node pre_Out:
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
     torch.Size([32, 32, 16, 16])
  Node_5 Out:   1 x torch.Size([32, 32, 16, 16])

Cell_4 Out: torch.Size([32, 128, 16, 16])

Cell_5:========================
Cell_5 In:  torch.Size([32, 128, 16, 16]) torch.Size([32, 128, 16, 16])

Preproc0_in:  torch.Size([32, 128, 16, 16]), Preproc1_in: torch.Size([32, 128, 16, 16])
Preproc0_out: torch.Size([32, 64, 16, 16]), Preproc1_out: torch.Size([32, 64, 16, 16])

  Node_0 In:    1 x torch.Size([32, 64, 16, 16])
  Node_0 Out:   1 x torch.Size([32, 64, 16, 16])

  Node_1 In:    1 x torch.Size([32, 64, 16, 16])
  Node_1 Out:   1 x torch.Size([32, 64, 16, 16])

  Node_2 In:
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 16, 16])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_2 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_3 In:
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_3 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_4 In:
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_4 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_5 In:
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 16, 16])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_5 Out:   1 x torch.Size([32, 64, 8, 8])

Cell_5 Out: torch.Size([32, 256, 8, 8])

Cell_6:========================
Cell_6 In:  torch.Size([32, 128, 16, 16]) torch.Size([32, 256, 8, 8])

Preproc0_in:  torch.Size([32, 128, 16, 16]), Preproc1_in: torch.Size([32, 256, 8, 8])
Preproc0_out: torch.Size([32, 64, 8, 8]), Preproc1_out: torch.Size([32, 64, 8, 8])

  Node_0 In:    1 x torch.Size([32, 64, 8, 8])
  Node_0 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_1 In:    1 x torch.Size([32, 64, 8, 8])
  Node_1 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_2 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_2 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_3 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_3 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_4 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_4 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_5 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_5 Out:   1 x torch.Size([32, 64, 8, 8])

Cell_6 Out: torch.Size([32, 256, 8, 8])

Cell_7:========================
Cell_7 In:  torch.Size([32, 256, 8, 8]) torch.Size([32, 256, 8, 8])

Preproc0_in:  torch.Size([32, 256, 8, 8]), Preproc1_in: torch.Size([32, 256, 8, 8])
Preproc0_out: torch.Size([32, 64, 8, 8]), Preproc1_out: torch.Size([32, 64, 8, 8])

  Node_0 In:    1 x torch.Size([32, 64, 8, 8])
  Node_0 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_1 In:    1 x torch.Size([32, 64, 8, 8])
  Node_1 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_2 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_2 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_3 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_3 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_4 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_4 Out:   1 x torch.Size([32, 64, 8, 8])

  Node_5 In:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node pre_Out:
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
     torch.Size([32, 64, 8, 8])
  Node_5 Out:   1 x torch.Size([32, 64, 8, 8])

Cell_7 Out: torch.Size([32, 256, 8, 8])

CNN Out:  torch.Size([32, 10])

离散网络结构

每个Node取结构参数最大的2个操作，构造离散的网络结构

// epoch_49.json
{
  "normal_n2_p0": "sepconv3x3",
  "normal_n2_p1": "sepconv3x3",
  "normal_n2_switch": [
    "normal_n2_p0",
    "normal_n2_p1"
  ],
  "normal_n3_p0": "skipconnect",
  "normal_n3_p1": "sepconv3x3",
  "normal_n3_p2": [],
  "normal_n3_switch": [
    "normal_n3_p0",
    "normal_n3_p1"
  ],
  "normal_n4_p0": "sepconv3x3",
  "normal_n4_p1": "skipconnect",
  "normal_n4_p2": [],
  "normal_n4_p3": [],
  "normal_n4_switch": [
    "normal_n4_p0",
    "normal_n4_p1"
  ],
  "normal_n5_p0": "skipconnect",
  "normal_n5_p1": "skipconnect",
  "normal_n5_p2": [],
  "normal_n5_p3": [],
  "normal_n5_p4": [],
  "normal_n5_switch": [
    "normal_n5_p0",
    "normal_n5_p1"
  ],
  "reduce_n2_p0": "maxpool",
  "reduce_n2_p1": "avgpool",
  "reduce_n2_switch": [
    "reduce_n2_p0",
    "reduce_n2_p1"
  ],
  "reduce_n3_p0": "maxpool",
  "reduce_n3_p1": [],
  "reduce_n3_p2": "skipconnect",
  "reduce_n3_switch": [
    "reduce_n3_p0",
    "reduce_n3_p2"
  ],
  "reduce_n4_p0": [],
  "reduce_n4_p1": [],
  "reduce_n4_p2": "skipconnect",
  "reduce_n4_p3": "skipconnect",
  "reduce_n4_switch": [
    "reduce_n4_p2",
    "reduce_n4_p3"
  ],
  "reduce_n5_p0": [],
  "reduce_n5_p1": "avgpool",
  "reduce_n5_p2": "skipconnect",
  "reduce_n5_p3": [],
  "reduce_n5_p4": [],
  "reduce_n5_switch": [
    "reduce_n5_p1",
    "reduce_n5_p2"
  ]
}

Conclusion

  • 提出了DARTS，一种简单高效的CNN和RNN 结构搜索算法，并达到了SOTA

  • 较之前的方法的效率提高了几个数量级


未来改进：

  • 连续结构编码与离散搜索之间的差异
  • 基于参数共享的方法？

Summary


Reference

【论文笔记】DARTS: Differentiable Architecture Search

论文笔记：DARTS: Differentiable Architecture Search

PyTorch 中的 ModuleList 和 Sequential: 区别和使用场景

DARTS代码分析

nni-Search Space-Mutable

nni-Mutable

posted @ 2020-05-24 19:20  ChenBong  阅读(840)  评论(1)  编辑  收藏  举报