折腾的心，颤抖的手，只因在 main 函数中执行了一次 int 强转 byte 的操作，输出结果太出所料，于是入坑，钻研良久，遂有此篇。
我们都知道，Java中有8中基本数据类型，每种类型都有取值范围，比如 1 个字节的 byte 取值范围是【-128~127】，4 个字节的 int 取值范围是 【-231~231-1】。因为能表示的值的范围不同，如果我们将 int 类型强转为 byte 类型的话，是很可能损失精度的，比如：
byte a = (byte) 127; // a = 127 byte b = (byte) 128; // b = -128 byte c = (byte) 256; // c = 0
以人脑的主观意识，128 只比 byte 范围上限多 1 而已，如果损失精度，把多的 1 舍去变 127 就好了啊，怎么就变成了 -128？也曾看到一些园友说，这种强转造成的精度损失后的结果是毫无意义的，博主不以为然；稍微深究一下，你会发现，这结果并不是编译器随便给的数字，而是经过逻辑运算后的结果——虽然，表面上你看不出这种结果有什么运算逻辑，但你不要忘了，计算机的逻辑都是二进制逻辑，不是你我的人脑逻辑啊。
二进制
二进制，是计算机唯一能识别、存储的数，用0和1两个数码来表示，基数为2，“逢二进一”，”借一当二”。
要搞清楚上面 Java 代码的运算逻辑，我们首先要做的是将对我们人脑直观的十进制数字转换成对计算机直观的二进制，这里就用到了一个概念叫比特位（bit），这是计算机最小的存储单元了，表示二进制的存储位。而我们说 一个字节占用 8 个长度位，就是指一个字节占用了八个比特位的长度，也就是八个二进制位。布衣博主画了一份草图，来将上文中的十进制数转换成二进制比特存储位，这里先以十进制的 256 为例：
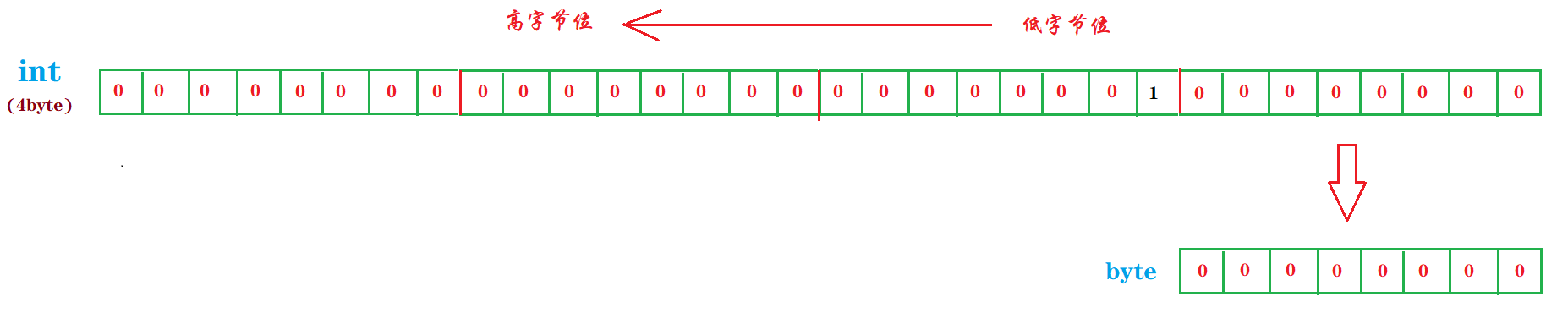
将4字节的int类型数据转换成单字节的byte，最高位的三个字节的存储单元将被舍弃掉，这才是损失精度的要义所在！所以，根据上图高位舍弃的强转后，你自己也可以看出来，最后得到的 byte 十进制表示数字 0 。嗯，似乎也就那么回事，还是很好理解，但是，沿用上面的图，我们换成 128 试试？
看草图，似乎也很简单，128强转后，按照高位舍弃理论，无非是舍弃掉了高字节位无意义的 24 个 0 而已，最后的 byte 字节表示的还是原来那么大，还应该是 128 才对啊，为什么实际程序运行的结果却变成了 -128 ？ 咳咳！老师有没有告诉过你，Java的数据是带符号的？你知道二进制中如何表示一个数的正负的吗？所以，上诉理论中，我们还遗漏了一个很重要的知识点，那就是符号位的表示。对于有符号二进制来说，为了区分数的正负，约定以最高位作为符号位，0表示正数，1 表示负数，除去符号位剩下的就是这个数的绝对值部分：
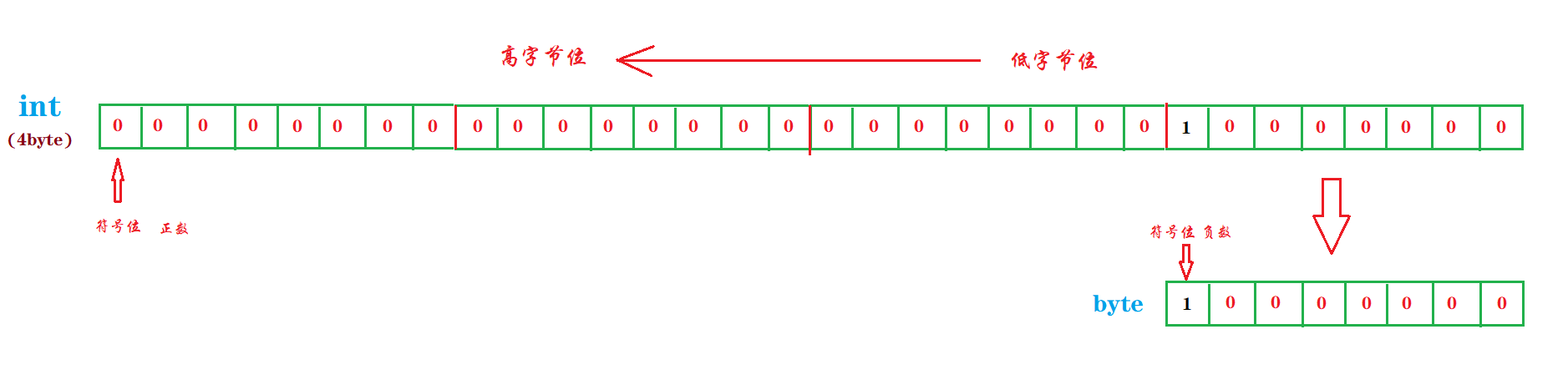
我们带上符号位，回过头来重新分析上面对 128 的强转：当高位的三个字节被舍弃掉之后，连同舍弃的还有它的符号位 0 ，最终的结果就是强转成单字节后，原来表示数值部分的 1 变成了符号位，表示为负，除去符号位，能表示值的就只有后7位的 0000000 了。这样表示的十进制值为 -0，在带符号的二进制中，-0 被规定用来指代 -128，+0 才表示 0 。看来，只要带上符号位，本文最开始的输出结果是很好分析的。至此，我们引出了二进制中的符号位，并用此解答了本文一开始的疑惑。但是，有了符号位，这里又有疑问了，如果符号位占据了字节高位（第一位），当我们在进行算数运算的时候，符号位又该如何处理呢？
原码、反码和补码
虽然人类用计算器算账的时候，是按十进制的思维来进行加减乘除的，但是对于计算机来说，它最终会将人类的输入转化成底层的二进制来操作。如果我们的二进制操作都是带符号的，这就会有上面提到的符号位该如何处理的问题。比如 5-3，21-25，21+15，-3-8 等等，两个数字相加减，结果可能是正数也可能是负数，如果将符号位加入运算，如何进行进位和借位操作？如果符号位不加入运算，单独区分符号位肯定会增加计算机底层设计的复杂度。不管怎样，有一点可以肯定，那就是带符号的二进制数是不能直接拿来运算的！肿么办呢？为了不增加计算机底层设计的复杂度，人类还是决定在符号位上下功夫，于是有了我们熟知的二进制领域中的 原码，反码以及补码等等概念，下面是三种码基本的表示的方法：
- 原码：符号位（字节序列的最高位）加上原数值绝对值的二进制表示；
- 反码：正数的反码是其本身，负数的反码为保持符号位不变其余位置按位取反；
- 补码：正数补码依旧是其本身，负数补码为反码加1；
其实，引入反码，我么已经可以将减法统一变作加法【 1-1=1+（-1）】进行正确的计算了，已经解决了符号位的问题了，但会产生 -0 和 +0 的问题，也就是 0 被带上了符号。虽然在人脑看来是正负 0 一样的，但是计算机可不那么认为，而且按照定义 0 会有两种原码表示，即 000 0000 和 1000 0000，这显然是有问题的。于是在反码的基础之上加 1 变补码，彻底解决了正负 0 的问题，以前表示 -0 的1000 0000 现在可以用来表示 -128，因为 -128 = -1-127=（-1）+（-127）=（1111 1111）补+（1000 0001）补=1000 0000。——这也是带符号位二进制能够多表示一个数的原因。下面是博主探究二进制运算的过程中画的原码和补码计算的结果差异图：
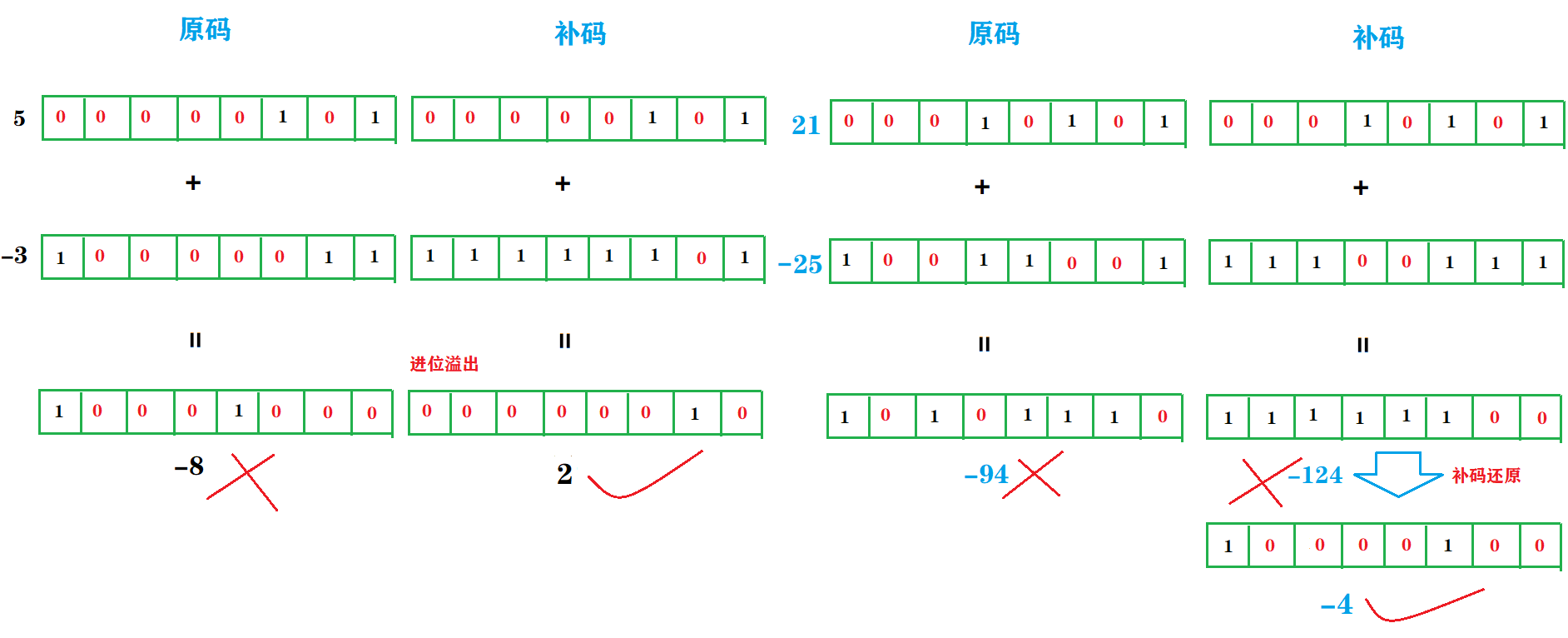
上图至少说明了两点：
第一，带符号二进制直接用原码进行加减运算特别不靠谱，而通过补码进行加法(减也看作加)运算很靠谱；
第二，如果运算结果是正数，由于正数的原码和补码相同，所以结果和十进制数是正确匹配的，如果结果是负数，需要将补码转成原码方能匹配正确的十进制结果；
虽然补码解决了问题，但是博主还是有疑问——难道计算机科学家是先知，他们怎么知道将原码求反码后再加 1 得到的补码就能够解决符号位的运算问题？感觉像是碰巧一样，毫无道理嘛！但正确无比的结果又似乎在告诉我，补码的产生背后，肯定有某种隐含的逻辑。。。（思考ing）。。。补码补码，为什么叫补码，没学过计算机的我只听过补数啊？咦，会不会和补数有关系呢，不然为什么都姓 补 呢？一番琢磨，卧槽，还真的有关系。在十进制中，如果两个数相加能凑成十或成百的整数，我们就可以把其中一个数叫另一个数的补数，因此可以说 4 和 6 互为补数；同样的对于二进制来说，我们也是可以凑个整数的，凑整就有补数，而补数对于运算往往大有帮助！这里拿一个 4 位二进制来说，若不考虑符号位，其能表示的最大数为 1111，包含 0 在内总共能表示 16 个数，那么这个 16 就是一个 整数。如果要计算 7-3，我们可以尝试带入补数的思想，先用 7 加 3 的补数 13 看会有什么发现。这是很简单的算术问题， 7+13 等于 20，和 7-3 的结果 4 差的有点远。但是，差的是什么呢？恰好就是我们前面提到的那个整数啊，如果我们用 20 减掉整数 16，恰恰就是我们要的结果 4 ！巧合吗？这可不是巧合，这是因为 20 已经超出了4 位二进制所能表示的最大数，产生进位溢出，这个溢出的数刚好就是那个整数 16。换成二进制表示你一定就了然了：
7-3 = 0111-0011=0111+1101=0100（10100进位溢出舍弃高位的1）
如果你还是不太理解，那么，博主将上面表述中特意强调的整数换成计算机术语中更常用的 模 你应该就恍然有感了。为什么上述中的整数也可以表述成模呢？因为二进制的进位溢出其实同模运算中遇整舍弃只留余数是一样的道理。具体到生活中我们可以用时钟来作比。时针在表盘上走一圈是12个点，因此 12 这个整就是一个模长，如果现在时针停在 12 点处，要让它指向 10 点，可以怎么做？顺时针（+）走10个点也行，逆时针（-）回 2 个点也行，而恰好 10 和 2 之间是互补的，于是，根据模长和补数的关系，我们就成功的将减法转换成了加法运算，这就是为什么上面的 7-3 可以换成 7+13的原因，由此可见，在带符号二进制的算数运算中，引入补码，其意思很明确，就是为了统一运算符。
回过头来可以解答开头的问题——为什么科学家先知一样的就知道负数的补码是其反码加 1 呢？ 根据博主对补数和模的粗浅解释，我们可以自己来算下。带符号的 4 位 二进制能表示的最大数是 7，最小数是 -8，模长依然是 16。在这个单字节范围内的负数，比如 -3 ，二进制表示为 1011 。以上面博主说过减法变加法的方式，取 3 的补数 13，二进制表示为 1101，这不正是 -3 的补数嘛！所以，负数的补码真不是科学家先知一般知道就是反码加 1，只不过运算出来恰好就是反码加 1 ，这也是算出补码最简单的方法了，于是也就那样去表述，并不是理论基础。
位运算
二进制的运算其实还不止于上面看到的基本的算数运算，还有一种运算叫逻辑运算——直接操作二进制中的位，而不涉及算术运算中的进位和借位，所以也叫位运算。面试你可能遇到过诸如 "写出 2*8 最有效率的运算方法"之类的问题，无非就是考你对于底层二进制的熟悉程度。不用说，当然是用位运算效率最高咯。所以，掌握一点位运算，在一些问题解决上，常常会有一些巧技（延伸阅读）。博主简述一下常见的逻辑运算，为最后的阐述做铺垫。
按位与（&）
相对应的二进制位同为 1 结果才为 1，否则都是 0，形如：0&0=0,0&1=0,1&0=0,1&1=1 。 利用这个特性，我们判断奇偶数就可以不用再传统的 n%2的方式了，直接用 n&1，结果为 1 就是奇数，为 0 就是偶数。why? 因为 0或正数，补码和原码相同，由于 1 的前 n 位都是 0 ，与 1 相与，结果肯定是 0 ，我们只关心最后一位，奇数肯定是 1，1与1相与结果为1；若为负数，原码转反码时，奇数最后一位由 1 变 0，但转补码后有加 1 操作，末尾为 1 ，判定同理。
按位或（|）
相对应的二进制位只要有一个为 1 ，结果即为 1，形如：0|0=0,0|1=1,1|0=1,1|1=1。
按位异或（^）
相对应的二进制位数字不同，结果为 1 ，否则都是 0 ，形如：0^0=0,0^1=1,1^0=1,1^1=0。异或有个特性就是，任何数与 0 异或，结果都是其本身。利用这个特性，可用于数的交换，以此可以解决一些面试***难：如何在不采用临时变量的情况下实现两个数的交换？当然，不用位运算也是可以实现的，只是不那么高级。常见写法奉上：
int a = 2; int b = 3; //方式一 a=a+b; b=a-b; a=a-b; // 方式二 a=a^b; b=a^b; a=a^b;
取反（~）
二进制位按位取反，0 变 1 ，1 变 0 。
左移（<<）
形如 a<<b，将 a 的各二进制位整体向左移 b 位，高位溢出位移出，低位补 0。在数值没有溢出的情况下，左移n位相当于乘 2 的n次方。例如 2<<3，即由二进制的 00000010 变成了 0010000，相当于 2 乘 2 的 3 次方，结果为 16。因为位运算是 CPU 直接支持的，这也就是上面提到的 2*8 最有效率的运算方法了。
右移（>>）
形如 a>>b ，原理同左移，只不过由于符号位在最高位，所以，如果右移的是负数，会在高位补 1 ，如果为正数，高位补 0 。
无符号右移（>>>）
与右移唯一的不同在于，不论原来最左边是什么数，移动后都在高位补 0。注意，没有无符号左移， 因为左移始终是在右边补 0 ，而符号位在左边，不存在补符号位的问题。
终章
哔哔了这么多，还是回到开始吧。看了博主上面无头无脑的分析，相信你早已明白，长字节的数要往短了转，直接强来，肯定是不行的。那就不转呗，反正也很少遇到。NO,NO,NO！只需要翻看一下Java的IO包中的各种输入输出流的读写方法，就可以发现，很多参数都是字节数组，因为字节可以说是计算机中能表示信息含义的最小单位了，尤其在网络编程中，为了不同通讯终端的数据兼容，发送和接受的数据基本都是字节序列，所以，知道如何将长字节数变短，也是很有必要滴。
那么，在Java中，我们怎么将一个int类型，转换成byte 还能成功的还原呢？直接强转，超过范围的部分，肯定是装不下的，不过我们知道，一个 int 占用 4个 byte，换句话说，我们可以用一个长度为 4 的 byte数组来装：
看图就知道，装进byte数组是容易的（这里的装法也可以反序来，即byte[0]装低8位，以此类推，还原相应调整顺序，只要明白原理，都OK），主要的问题在于如何将 int 拆分成单个字节放进数组。看图就知道，其实也比较简单，就是进行位运算中的右移（>>）操作，不然博主上面位运算铺垫个铲铲啊，不多说，代码一目了然：
public static byte[] int2Bytes(int i) { byte[] bytes = new byte[4]; bytes[0] = (byte) (i >> 24); bytes[1] = (byte) (i >> 16); bytes[2] = (byte) (i >> 8); bytes[3] = (byte) i; return bytes; }
装是装进去了，怎么还原呢？我们刚刚是进行了进行了右移操作，要还原的话，很自然的我们想到要左移（<<），稍微有点位运算基础，似乎实现起来也简单：
public static int bytes2Int(byte[] bytes) { // 左移将原来的数先还原到对应的位置，再 按位或 将几个数进行合并 return bytes[3] | bytes[2] << 8 | bytes[1] << 16 | bytes[0] << 24; }
如果你真这样搞，那就等着大大的bug吧！如上图博主画图是 256 的二进制存储位序列图，用上面的方法还原出来倒是没问题，你多换几个数试试，比如-258， 245677，-2677等等？这都是博主随便举的数字，没有啥特殊，但结果会让你大跌眼镜。为什么通过右移装进数组再按照同样的思维方式左移还原就不行了呢？那是因为计算机对二进制的运算和存储都是以补码方式来进行的啊，亲。-258 在 int 中存的样子不是你以为的这个样子：
而应该是下面这个样子：
因此，我们装到字节数组中的就是第二份草图中存储位序列中的每一个字节段。而当我们用左移想进行还原的时候，byte 数组中每个byte左移后的结果其实是下面这样的：
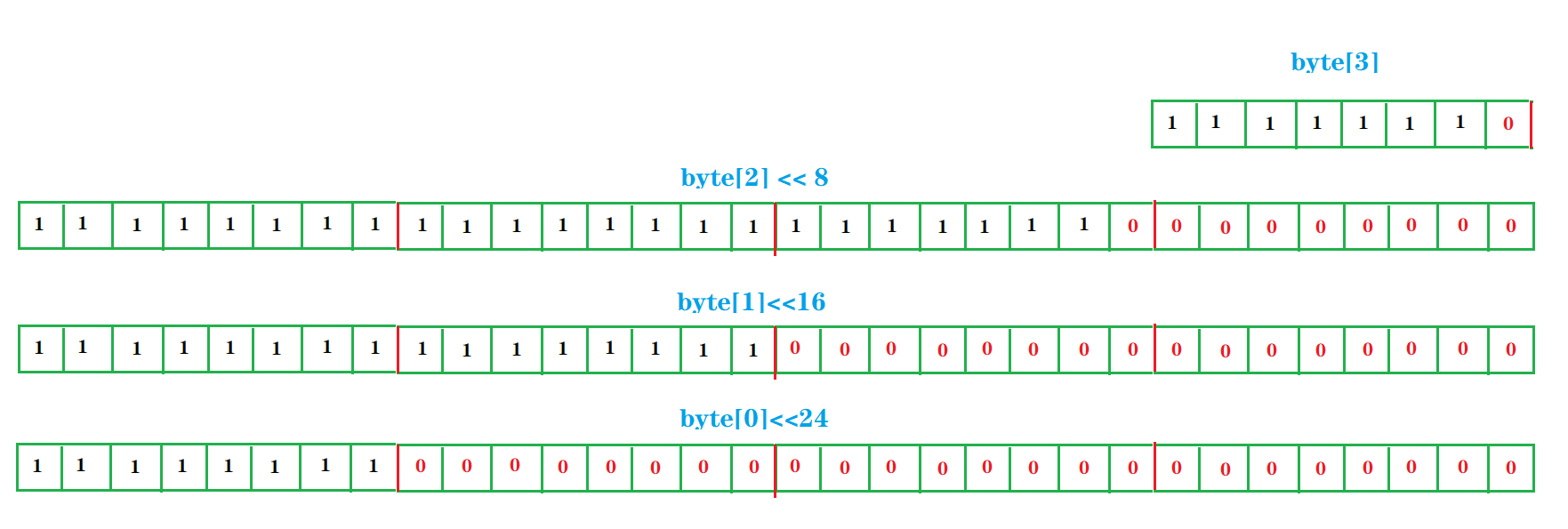
对于上面的草图，博主解释一下。在进行移位运算时，byte，short，char 的类型会提升为 4 字节 32 位的 int 型，就需要用 0 或 1 进行补位，如果是负数，会在前面补 1 ，如果是正数则补 0 。从上图左移补齐后的存储序列来看，如果此时将得到的 4 个 int 值进行 按位或（|）操作（未移位的byte[3]此时也会补位到 32 位），结果就是下面这样：
哇，这个结果，看起来这个数好大的样子，其实不大，因为博主早就说过了计算机是以补码的形式存储二进制的，将该补码转回原码你会发现，才等于 -2 ，挺小的，不过和原来的 -258相差太多了。分析下来，其实你已经发现了，还是因为符号位在捣乱：当还原前字节数组中有负数的时候，在提升为 int 补位的时候补1 就补出了问题。如何解决呢，很简单，将负数本来补的 1 置为 0 。通常的做法是采取将字节数先和 0xff（00000000 00000000 00000000 11111111）进行 按位与（&）操作，在电计算机补 1 之前，我们自己先给补 0 到32位，形如布衣草图：
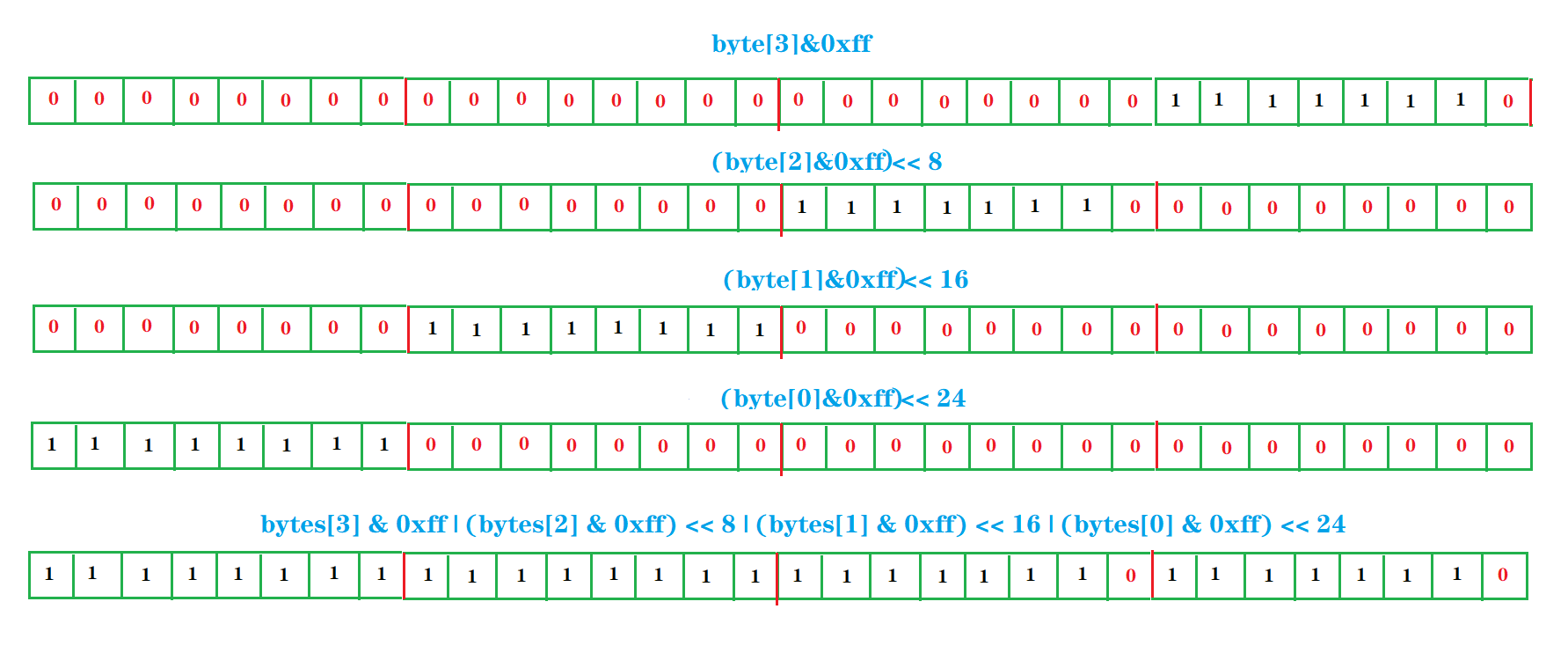
所以，上面还原 int 的方法该这样写：
public static int bytes2Int(byte[] bytes) { return bytes[3] & 0xff | (bytes[2] & 0xff) << 8 | (bytes[1] & 0xff) << 16 | (bytes[0] & 0xff) << 24; }
好了，结尾勿煽情，哔完收工！若博主阐述有不恰当的地方，欢迎留言指正；推不推荐的，随缘随便随你吧。
