算法与数据结构 6 - 进阶一

前言

闻道于 GTYZ，说，作此篇。

目录

• 势能线段树
  • 介绍
  • 例题
• 01 Trie
  • 介绍
  • 变体一：可持久化 01 Trie
  • 变体二：“满子树压缩” 01 Trie
  • 例题
• 平衡树 FHQ-Treap
  • 介绍
  • 变体一：带标记的 Treap
  • 变体二：可持久化 Treap
  • 变体三：值域有交 Treap
  • 例题
• 参考资料

0x01 势能线段树

介绍

势能线段树时间复杂度的正确性来源于势能的总大小可以接受。简单来说，就是多次操作会使得该操作失效。
例如，单次区间开根的时间复杂度很高，但同一个数被多次开根会使其迅速变为 \(1\)。而 \(\sqrt{1}=1\)，所以操作“失效”了。

\(\sqrt{1145141910810}=1070113\)
\(\sqrt{1070113}=1034\)
\(\sqrt{1034}=32\)
\(\sqrt{32}=5\)
\(\sqrt{5}=2\)
\(\sqrt{2}=1\)
（以上结果均已向下取整）

例题

上帝造题的七分钟 2 / 花神游历各国
TEST_69

0x02 01 Trie

介绍

01 Trie 主要用来解决和二进制位运算有关的问题。将数的二进制表示看做一个字符串，就可以建出字符集为 \(\{0,1\}\) 的 Trie。

变体一：可持久化 01 Trie

参考主席树。这里不再展开。

变体二：“满子树压缩” 01 Trie

意思是将 Trie 上的满子树用一个点代替。

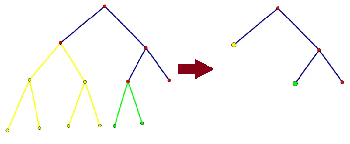
由于 01 Trie 是二进制对齐的，因此可以用单个节点表示形如区间 \([2^kp,2^k(p+1)-1]\) 这样的区间中的所有信息。

例题

魔法手杖
最大异或和
Cowmistry P

0x03 FHQ-Treap

介绍

FHQ-Treap 是一种常用 Treap。详细资料可参阅往期文章。

变体一：带标记的 Treap

和线段树类似。当需要进行区间操作时，为降低均摊复杂度，可以使用标记暂停递归。

变体二：可持久化 Treap

参考主席树。这里不再展开。

变体三：值域有交 Treap

考虑将“优先级”更高的 Treap 按权值拆分为两儿子，并分别于“优先级”更低的 Treap 进行合并。

例题

普通平衡树
文艺平衡树
可持久化平衡树
线段树分裂

参考资料

[1] 2025广东省集Div2数据结构1
[2] 数据结构 Trick 之：平衡树有交合并
[3] 均摊复杂度·势能分析
[4] 字典树 (Trie)·维护异或极值