Codeforces 1450 题目研讨
本文将会对 Codeforces 1450 A-H 进行探讨。
题目链接
题目分析
A
难度：入门
算法标签：字符串
题目描述：对给定的字符串内字符的顺序进行调换，使 trygub 不是该字符串的子串。
解题思路：
本题有多种思路。下面介绍其中两种。
- 将字符串内所有
b字符移到字符串开头 - 对字符串进行排序
容易证明这两种方法都是正确的。
B
难度：普及−
算法标签：贪心（？）
题目描述：平面上有 \(n\) 个点。每次操作选择一个点，将到这个点的曼哈顿距离不超过 \(k\) 的点删除。问最少多少次操作后平面上只剩下一个点，或者无法做到这一点（此时输出 \(-1\)）。
解题思路：答案必然 \(\in \{-1, 1\}\)。证明如下：
用反证法。假设存在一种情况使得最优解为 \(t\) 且 \(t \ge 2\)。设第 \(t-1\) 次操作选择点 A，则分类讨论：
- 若第 \(t\) 次操作选择点 A，则情况不会有任何变化（因为前一次操作已经清空了 A 周围的点），与“最优解为 \(t\)”矛盾；
- 若第 \(t\) 次操作不选择点 A，则点 A 一定不会被删除，因为其他点到 A 的距离一定大于 \(k\)，不满足结束条件，矛盾。
综上所述，不存在情况使得最优解为 \(t\) 且 \(t \ge 2\)。因此 \(t\in \{-1, 1\}\)。
\(O(Tn^2)\) 判断即可。
C1 + C2
难度：普及+/提高 - 提高+/省选−
算法标签：构造、数学
题目描述：
有一个 \(n\) 行 \(n\) 列的井字棋棋盘，棋盘中的每一个格子要么是空的，要么包含一个棋子。 这里有两种棋子分别为 X 和 O 。如果有三个同种类的棋子连续横着或竖着排列，则称这是获胜局。（注意：斜着不算） 如果棋盘中没有这样的连续三个同种类的排列，则称这是一个平局。
在一次操作中，你可以将某一枚棋子替换为另一颗棋子。令 \(k\) 为初始棋盘中棋子的总数，你可以做最多 \(\lfloor\frac{k}{3}\rfloor\) 次上述操作使得最后的局面为平局。注意：你不需要最小化操作次数。
C1 与 C2 的不同在于 C2 的初始棋局中含有两种棋子，而 C1 只有一种。
解题思路：
注意到斜线不算三连，因此考虑构造斜线。
将格子分为三种，第 \(i(i\in\{0, 1, 2\})\) 种格子的坐标 \((x, y)\) 满足 \((x+y)\%3=i\)。于是任意的横竖三连都被拆分为三部分。由于每种格子互相不连续，因此每种格子内部可以由相同的棋子构成。于是棋盘三染色，枚举其中两种，每次操作令两种颜色格子上的棋子不同。由抽屉原理可知答案合法。
D
难度：普及+/提高
题目描述：
给定长度为 \(n\) 的序列 \(a\) 和正整数 \(k\)，以如下方式生成 \(b\)：
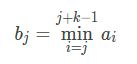
给定 \(a\)，求有哪些 \(1 \le k \le n\)，使得生成的 \(b\) 是一个排列。
解题思路：
\(k=1\) 或 \(n-1\) 时特判。
不难发现对于 \(k=n-1\)，当 \(1\) 和 \(2\) 分别位于整个 \(a\) 的两头才合法。
对于 \(k=n-2\)，同样要求 \(1\) 在序列头部和尾部之一，而 \(2\) 需要在序列去除 \(1\) 后的部分的头围之一;
对于 \(k\in[2, n-3]\)，同理可得：每次递归地判断当前数字在剩余区间内是否在头尾。
另外注意到：当 \(k(k > 2)\) 不合法时，\(k-1\) 也不合法。
因此有分类讨论：对于 \(k=1\) 特判，对于 \(k>1\) 递归求解。
E
难度：省选/NOI−（个人感觉评高了）
算法标签：差分约束、图论
题目描述：
整个社会可以用一张由 \(n\) 个顶点和 \(m\) 条边组成的无向联通图来表示。顶点代表人，一条边 \((i,j)\) 代表人 \(i\) 和 \(j\) 之间的友谊。
在社会上，第 \(i\) 个人有收入 \(a_i\)。一个人 \(i\) 羡慕一个人 \(j\)，等价于 \(j\) 比 \(i\) 多出1个单位的收入，也就是 \(a_j=a_i+1\)。
如果对于每一对朋友，都有一个人羡慕另一个人，这个社会就叫资本主义社会。对于一些朋友关系，你知道哪个人在羡慕另一个人。对于其余的朋友关系，你不知道谁羡慕谁。
社会收入不等值的定义是：\(\max_{i=1}^na_i - \min_{i=1}^na_i\)，也就是社会中收入最多的人的收入与收入最少的人的收入之差。
你只知道一些朋友关系，不知道每个人的收入。对于一部分朋友关系，你知道谁羡慕谁；对于另外一部分，你不知道。你要判断这个社会是否可能成为资本主义社会。如果是，你要构造一个 \(a\) 满足所有条件，且这是个资本主义社会。要求你给出的 \(a\) 让社会收入不等值最大。
解题思路：
不难发现当图中有奇环时无解。而当图中没有奇环时可以转换为差分约束。此时可以跑 Floyd 然后找到极差最大的那一组解。所以直接做就做完了。
F
难度：省选/NOI−
