hdu 6161--Big binary tree(思维--压缩空间)
Problem Description

You are given a complete binary tree with n nodes. The root node is numbered 1, and node x's father node is ⌊x/2⌋. At the beginning, node x has a value of exactly x. We define the value of a path as the sum of all nodes it passes(including two ends, or one if the path only has one node). Now there are two kinds of operations:
1. change u x Set node u's value as x(1≤u≤n;1≤x≤10^10)
2. query u Query the max value of all paths which passes node u.
Input
There are multiple cases.
For each case:
The first line contains two integers n,m(1≤n≤10^8,1≤m≤10^5), which represent the size of the tree and the number of operations, respectively.
Then m lines follows. Each line is an operation with syntax described above.
For each case:
The first line contains two integers n,m(1≤n≤10^8,1≤m≤10^5), which represent the size of the tree and the number of operations, respectively.
Then m lines follows. Each line is an operation with syntax described above.
Output
For each query operation, output an integer in one line, indicating the max value of all paths which passes the specific node.
Sample Input
6 13
query 1
query 2
query 3
query 4
query 5
query 6
change 6 1
query 1
query 2
query 3
query 4
query 5
query 6
Sample Output
17
17
17
16
17
17
12
12
12
11
12
12
题意:有一棵 由 n 个节点构成的完全二叉树,节点编号1~n,对于i节点其父亲节点为i/2,并且其初始权值为 x ,现在有m次操作:1、修改节点 i 权值为 x 。 2、求经过i节点的所有路径中路径上节点最大权值和。
思路:由于n很大1e8,所以不能直接建树进行计算,不能建树怎么计算呢?发现询问的m为1e5 ,所以我们可以用map保存修改的节点。对于每次修改一个节点u时,我们可以计算并用map存下u的子树中从u到其叶子节点的最大权值和,并且向上搜索u的祖先节点,也用map存下相应的最大路径权值和。 对于询问经过 u 的最大的路径权值和,我们只需要从u向上搜索祖先节点即可。
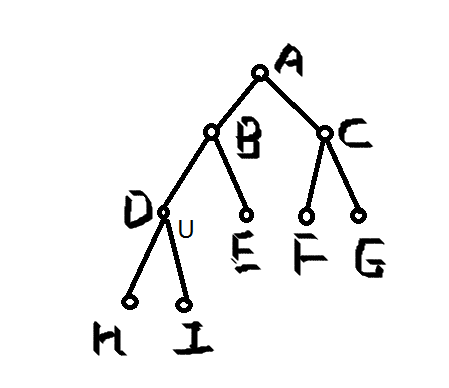
如求经过D的最大路径权值和。有以下的路径:1、起始为从D的叶子节点经D到D的另一个叶子节点。 2、从D的叶子节点经D B 到B的一个叶子节点。 3、从D的一个叶子节点经B D A 到A的一个叶子节点。所以求经过D的最大路径权值和时就是由D开始向上搜索D的祖先节点,进行计算。
代码如下:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <cmath> #include <map> using namespace std; typedef long long LL; map<int,LL>mp; map<int,LL>mx; LL ans; int n,m; int pos[100]; void init() { int tmp=n; int deep=(int)log2(n)+1; for(int i=deep;i>=1;i--) { pos[i]=tmp; tmp>>=1; } } void cal(int x) { if(mp.count(x)) return ; if(x>n) { mp[x]=0; return ; } int deep=(int)log2(x)+1; LL tmp=0; for(int i=x;i<=n;i=(i<<1|1)) tmp+=i; if(pos[deep]==x){ LL sum=0; for(int i=deep;;i++) { sum+=pos[i]; if(pos[i]==n) break; } tmp=max(tmp,sum); } mp[x]=tmp; } void update(int x) { if(!x) return ; LL y; if(mx.count(x)==0) y=x; else y=mx[x]; cal(x<<1); cal(x<<1|1); mp[x]=max(mp[x<<1],mp[x<<1|1])+y; update(x>>1); } void query(LL sum,int x,int son) { if(!x) return ; cal(x<<1); cal(x<<1|1); if(!mx.count(x)) mx[x]=x; ans=max(ans,sum+mp[son^1]+mx[x]); sum+=mx[x]; query(sum,x>>1,x); } int main() { char s[10]; while(scanf("%d",&n)!=EOF) { init(); mp.clear(); mx.clear(); scanf("%d",&m); while(m--) { scanf("%s",s); if(s[0]=='q') { int x; scanf("%d",&x); cal(x<<1); cal(x<<1|1); if(!mx.count(x)) mx[x]=x; ans=mp[x<<1]+mp[x<<1|1]+mx[x]; cal(x); query(mp[x],x>>1,x); printf("%lld\n",ans); } else { int x; LL y; scanf("%d%lld",&x,&y); mx[x]=y; update(x); } } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号