Dijkstra算法
对于普通的BFS算法,无法解决有权图中的最短路径问题,因为它不能保证处于队列前面的顶点是最接近源s的顶点,所以需要对BFS加以改进,保证每次访问的节点到源点的长度是最短的。
基本思想:
1.将图上的初始点看作一个集合S,其它点看作另一个集合
2.根据初始点,求出其它点到初始点的距离d[i] (若相邻,则d[i]为边权值;若不相邻,则d[i]为无限大)
3.选取最小的d[i](记为d[x]),并将此d[i]边对应的点(记为x)加入集合S
(实际上,加入集合的这个点的d[x]值就是它到初始点的最短距离)
4.再根据x,更新跟 x 相邻点 y 的d[y]值:d[y] = min{ d[y], d[x] + 边权值w[x][y] },因为可能把距离调小,所以这个更新操作叫做松弛操作。
(仔细想想,为啥只更新跟x相邻点的d[y],而不是更新所有跟集合 s 相邻点的 d 值? 因为第三步只更新并确定了x点到初始点的最短距离,集合内其它点是之前加入的,也经历过第 4 步,所以与 x 没有相邻的点的 d 值是已经更新过的了,不会受到影响)
5.重复3,4两步,直到目标点也加入了集合,此时目标点所对应的d[i]即为最短路径长度。
(注:重复第三步的时候,应该从所有的d[i]中寻找最小值,而不是只从与x点相邻的点中寻找。想想为什么?)
图解:(动图很快,不容易理解,最好结合上面的步骤自己画一个图,一步一步消化)
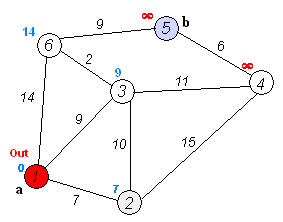
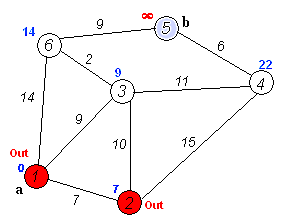
原理:Dijkstra的大致思想就是,根据初始点,挨个的把离初始点最近的点一个一个找到并加入集合,集合中所有的点的d[i]都是该点到初始点最短路径长度,由于后加入的点是根据集合S中的点为基础拓展的,所以也能找到最短路径。算法实现方面可以使用堆优化,堆优化的主要思想就是使用一个优先队列(就是每次弹出的元素一定是整个队列中最小的元素)来代替最近距离的查找,用邻接表代替邻接矩阵,这样可以大幅度节约时间开销。
python代码实现:
#!/usr/bin/env python # -*- coding: utf-8 -*- # 定义不可达距离 _ = float('inf') # points点个数,edges边个数,graph路径连通图,start起点,end终点 def Dijkstra(points, edges, graph, start, end): map = [[_ for i in range(points + 1)] for j in range(points + 1)] pre = [0] * (points + 1) # 记录前驱 vis = [0] * (points + 1) # 记录节点遍历状态 dis = [_ for i in range(points + 1)] # 保存最短距离 road = [0] * (points + 1) # 保存最短路径 roads = [] map = graph for i in range(points + 1): # 初始化起点到其他点的距离 if i == start: dis[i] = 0 else: dis[i] = map[start][i] if map[start][i] != _: pre[i] = start else: pre[i] = -1 vis[start] = 1 for i in range(points + 1): # 每循环一次确定一条最短路 min = _ for j in range(points + 1): # 寻找当前最短路 if vis[j] == 0 and dis[j] < min: t = j min = dis[j] vis[t] = 1 # 找到最短的一条路径 ,标记 for j in range(points + 1): if vis[j] == 0 and dis[j] > dis[t] + map[t][j]: dis[j] = dis[t] + map[t][j] pre[j] = t p = end len = 0 while p >= 1 and len < points: road[len] = p p = pre[p] len += 1 mark = 0 len -= 1 while len >= 0: roads.append(road[len]) len -= 1 return dis[end], roads # 固定map图 def map(): map = [[_, _, _, _, _, _], [_, _, 2, 3, _, 7], [_, 2, _, _, 2, _], [_, 3, _, _, _, 5], [_, _, 2, _, _, 3], [_, 7, _, 5, 3, _] ] s, e = input("输入起点和终点:").split() dis, road = Dijkstra(5, 7, map, int(s), int(e)) print("最短距离:", dis) print("最短路径:", road) # 输入边关系构造map图 def createmap(): a, b = input("输入节点数和边数:").split() n = int(a) m = int(b) map = [[_ for i in range(n + 1)] for j in range(n + 1)] for i in range(m + 1): x, y, z = input("输入两边和长度:").split() point = int(x) edge = int(y) map[point][edge] = float(z) map[edge][point] = float(z) s, e = input("输入起点和终点:").split() start = int(s) end = int(e) dis, road = Dijkstra(n, m, map, start, end) print("最短距离:", dis) print("最短路径:", road) if __name__ == '__main__': map()
java实现:
PriorityQueue:
package com; //优先队列 public class PriorityQueue { private int size;//元素个数 private int capacity;//容量 private Entry[]arr;//保存元素 private int[]pos;//同步根据index和位置的对应关系 public PriorityQueue(int capacity) { this.capacity=capacity; arr=new Entry[capacity+1]; pos=new int[capacity+1]; } //添加一个节点 public void offer(int index,int dis) { if(size==0) { arr[++size]=new Entry(index,dis); pos[index]=size; }else { arr[++size]=new Entry(index,dis); pos[index]=size; int j=size; for(int i=j/2;i>0;j=i,i/=2) {//上滤 if(arr[j].dis<arr[i].dis) { Entry p=arr[i]; arr[i]=arr[j]; arr[j]=p; pos[arr[i].index]=i; pos[arr[j].index]=j; } } } } public int peek() {//获取头部元素 return arr[1].index; } //删除头部元素 public int poll() { Entry temp=arr[size]; int res=arr[1].index; --size; int j=1; int i=j*2; while(i<=size) {//下滤 if(i+1<=size&&arr[i+1].dis<arr[i].dis) { ++i; } if(arr[i].dis<temp.dis) { arr[j]=arr[i]; pos[arr[j].index]=j; j=i; i*=2; }else { break; } } arr[j]=temp; pos[arr[j].index]=j; return res; } //更新操作 public void increase(int index,int inc) { Entry temp=null; int i; // for(i=1;i<=size;++i) { // if(index==arr[i].index) { // temp=arr[i]; // break; // } // } i=pos[index]; temp=arr[i]; temp.dis+=inc; if(inc>0) {//下滤 int j=i; i*=2; while(i<=size) { if(i+1<=size&&arr[i+1].dis<arr[i].dis) { ++i; } if(arr[i].dis<temp.dis) { arr[j]=arr[i]; pos[arr[j].index]=j; j=i; i*=2; }else { break; } } arr[j]=temp; pos[arr[j].index]=j; }else {//上滤 int j; for(j=i,i/=2;i>0;j=i,i/=2) { if(temp.dis<arr[i].dis) { arr[j]=arr[i]; pos[arr[j].index]=j; }else { break; } } arr[j]=temp; pos[arr[j].index]=j; } } //优先队列中的节点类 public static class Entry{ int index; int dis; public Entry(int index,int dis) { this.index=index; this.dis=dis; } public int getIndex() { return index; } } public static void main(String[]args) { PriorityQueue pq=new PriorityQueue(20); pq.offer(1, 1); pq.offer(2, 2); pq.offer(3, 2); pq.increase(3, 1); pq.poll(); } }
Graph:
package com; import java.util.ArrayList; import java.util.Arrays; import java.util.LinkedList; import java.util.List; //图,使用邻接表存储 public class Graph { private int n; //the number of nodes public static final int INF=Integer.MAX_VALUE; List<List<Node>> table;//邻接表 public Graph(int n) { this.n=n; table=new ArrayList<List<Node>>(n+1);// the index 0 does not use; for(int i=0;i<n+1;++i) { table.add(new LinkedList<Node>()); } } //添加边 public void addEdge(int u,int v,int weight) {//u->v table.get(u).add(new Node(v,weight)); } //朴素的实现 public List<int[]>dijkstra1(int s){ int[]dis=new int[n+1]; int[]path=new int[n+1]; boolean[]mark=new boolean[n+1]; Arrays.fill(dis, INF); dis[s]=0; path[s]=0; for(int i=1;i<n;++i) { for(Node temp:table.get(s)) { if(dis[s]+temp.weight<dis[temp.index]) { dis[temp.index]=dis[s]+temp.weight; path[temp.index]=s; } } mark[s]=true; int minDis=INF,index=0; for(int j=1;j<=n;++j) { if(!mark[j]&&dis[j]<minDis) { minDis=dis[j]; index=j; } } s=index; } ArrayList<int[]>res=new ArrayList<int[]>(2); res.add(path); res.add(dis); return res; } //采用优先队列优化 public List<int[]>dijkstra2(int s){ int[]path=new int[n+1]; int[]dis=new int[n+1]; boolean[]mark=new boolean[n+1];//记录访问过的节点 Arrays.fill(dis, INF); dis[s]=0; path[s]=0; PriorityQueue pq=new PriorityQueue(n); for(int i=1;i<n;++i) { for(Node temp:table.get(s)) { if(!mark[temp.index]&&dis[s]+temp.weight<dis[temp.index]) { if(dis[temp.index]==INF) { dis[temp.index]=dis[s]+temp.weight; pq.offer(temp.index, dis[temp.index]); }else { pq.increase(temp.index, dis[s]+temp.weight-dis[temp.index]); dis[temp.index]=dis[s]+temp.weight; } path[temp.index]=s; } } mark[s]=true; s=pq.poll(); } ArrayList<int[]>res=new ArrayList<int[]>(2); res.add(path); res.add(dis); return res; } //递归获取路径信息 private List<Integer>getPath(int[]path,int s,int cnt) { if(cnt==s) { List<Integer>lt=new LinkedList<Integer>(); lt.add(s); return lt; } List<Integer>lt=getPath(path,s,path[cnt]); lt.add(cnt); return lt; } //打印路径信息 public void printPath(List<int[]>info,int s) { List<List<Integer>> pathInfo=new LinkedList<List<Integer>>(); for(int i=1;i<info.get(0).length;++i) { List<Integer>paths=getPath(info.get(0),s,i); int sz=paths.size(); System.out.print(paths.get(0)); for(int j=1;j<sz;++j) { System.out.print("->"+paths.get(j)); } System.out.println(" 距离:"+info.get(1)[i]); } } //图的节点类 private static class Node{ int weight; int index; public Node(int index,int weight) { this.index=index; this.weight=weight; } } }
StartUp:
package com; import java.io.FileNotFoundException; import java.io.FileReader; import java.util.List; import java.util.Scanner; //启动类,程序的入口 public class StartUp { public static void start() { try { Scanner scan=new Scanner(new FileReader("in.txt")); int t=scan.nextInt();//测试用例的数目 for(int i=0;i<t;++i) { int n=scan.nextInt();//节点数目 int m=scan.nextInt();//边的数目 int s=scan.nextInt(); Graph g=new Graph(n); for(int j=0;j<m;++j) { int u=scan.nextInt(); int v=scan.nextInt(); int w=scan.nextInt(); g.addEdge(u, v, w); } List<int[]>res=g.dijkstra2(s); g.printPath(res, s); } } catch (FileNotFoundException e) { e.printStackTrace(); } } public static void main(String[]args) { start(); } }
输入:
2 5 8 1 1 2 2 1 3 5 1 4 6 2 3 1 2 4 3 2 5 5 3 5 1 4 5 2 7 12 1 1 2 2 1 4 1 2 4 3 2 5 10 3 1 4 3 6 5 4 3 2 4 6 8 4 7 4 4 5 2 5 7 6 7 6 1
输出:
1 距离:0 1->2 距离:2 1->2->3 距离:3 1->2->4 距离:5 1->2->3->5 距离:4 1 距离:0 1->2 距离:2 1->4->3 距离:3 1->4 距离:1 1->4->5 距离:3 1->4->7->6 距离:6 1->4->7 距离:5


