算法16:Letcode_归并排序_相关面试题 (超难)
归并排序(Merge Sort)就是利用归并的思想实现排序方法。它的原理是假设初始序列含义n个记录,则可以看成是n个有序子序列,每个序列的长度为1,然后两两归并,得到【n/2】([x]表示不小于x的最小整数)个长度为2或1的有序咨询;再两两归并.......;如此重复,知道得到一个长度为n的有序序列为止,这种排序方法成为2路归并排序。
下面看一张图片,可以帮助我们更好的理解归并排序:
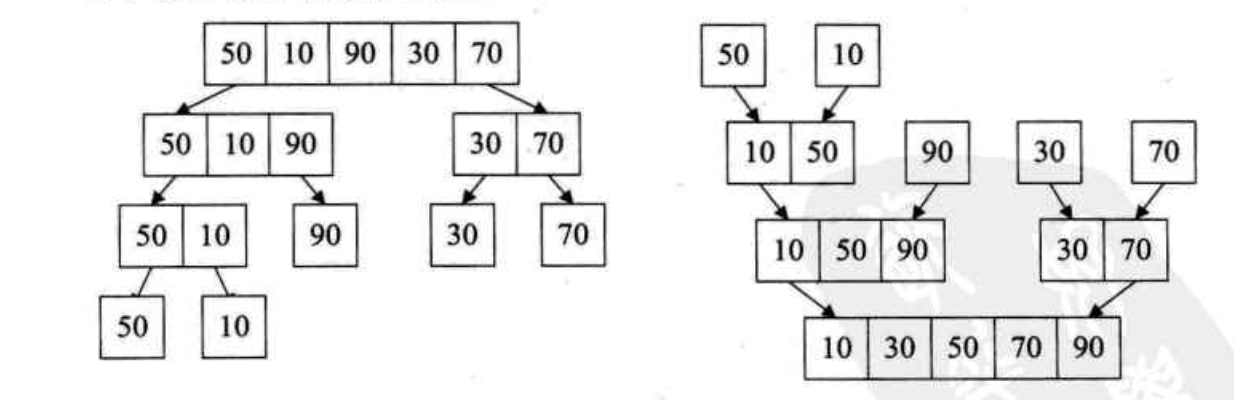
左侧是数组的初步拆分过程,右侧是逐步合并过程,并最终得到一个有序序列。
代码如下:
package code2.排序_03;
/**
* 归并排序
*/
public class Code01_MergeSort {
public void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
private void process (int[] arr, int left, int right)
{
if (left == right) {
return;
}
int mid = (left + right) >> 1;
process(arr, left, mid);
process(arr, mid + 1, right);
merge(arr, left, mid, right);
}
private void merge (int[] arr, int left,int mid, int right)
{
int[] help = new int[right - left + 1];
int p1 = left;
int p2 = mid +1;
int i = 0;
while (p1 <= mid && p2 <= right) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= right) {
help[i++] = arr[p2++];
}
for (int j =0; j < help.length; j++) {
arr[left+j] = help[j];
}
}
public static void main(String[] args) {
Code01_MergeSort sort = new Code01_MergeSort();
int[] arr = {8,6,7,9,10,5,7,3,2};
sort.printArray(arr);
sort.process(arr, 0, arr.length-1);
System.out.println("排序后:");
sort.printArray(arr);
}
}
如果代码看的有些吃力,可以结合下面我手绘的归并排序的过程进行理解
只会个归并排序,其实没啥意义。不仅仅是归并排序,任何算法都是一样的,我们必须要能够掌握原理,灵活运用才行。下面来看通过归并排序延伸出来的面试题。
面试题一:最小和问题
在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。
例子: [1,3,4,2,5]
1左边比1小的数:没有
3左边比3小的数:1
4左边比4小的数:1、3
2左边比2小的数:1
5左边比5小的数:1、3、4、 2
所以数组的小和为1+1+3+1+1+3+4+2=16
解题思路:
1. 普通两层遍历肯定是可以解出这道题的,但是两层遍历的时间的复杂度是O(N^2). 而归并排序的时间复杂度是 N*logN, 性能上更优。
2. 找到每个数左侧的比这个数小的数进行求和。变相也就是从左到右,找到当前数右侧比自己大的数出现了几次,出现一次,自己加一次。举个例子: 如果有序数组是{1,2,3,4}. 那么在我们从左到右遍历的时候,当前值为1,那么有3个值是比1大,因此1+1+1. 当前数为2时,有2个数比2大,那么 2 + 2. 如果当前数为3,值有一个数比3大,因此保留3. 最终的结果是1+1+1+2+2+3 = 10. 那么最终的最小和尾10. 代码如下:
package code2.排序_03;
/**
* 在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。
* 例子: [1,3,4,2,5]
* 1左边比1小的数:没有
* 3左边比3小的数:1
* 4左边比4小的数:1、3
* 2左边比2小的数:1
* 5左边比5小的数:1、3、4、 2
* 所以数组的小和为1+1+3+1+1+3+4+2=16
*/
public class Code02_SmallSum {
private int process (int[] arr, int left, int right)
{
if (left == right) {
return 0;
}
int mid = (left + right) >> 1;
return process(arr, left, mid) + process(arr, mid + 1, right) + merge(arr, left, mid, right);
}
private int merge (int[] arr, int left,int mid, int right)
{
int[] help = new int[right - left + 1];
int p1 = left;
int p2 = mid +1;
int i = 0;
int result = 0;
while (p1 <= mid && p2 <= right) {
result += arr[p1] < arr[p2] ? (right-p2+1)*arr[p1] : 0;
help[i++] = arr[p1] > arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= right) {
help[i++] = arr[p2++];
}
for (int j =0; j < help.length; j++) {
arr[left+j] = help[j];
}
return result;
}
public static void main(String[] args) {
Code02_SmallSum sort = new Code02_SmallSum();
int[] arr = {5,2,3,4,1};
//int[] arr = {1,2,3,4};
int smallSum =sort.process(arr, 0, arr.length-1);
System.out.println(smallSum);
}
}
面试题2:逆序对
在一个数组中,
任何一个前面的数a,和任何一个后面的数b,
如果(a,b)是降序的,就称为逆序对
返回数组中所有的逆序对
解题思路:上一题是找右侧比自己大的数,这一题则是找有侧比自己小的数。思路相同
package code2.排序_03;
/**
*在一个数组中,
* 任何一个前面的数a,和任何一个后面的数b,
* 如果(a,b)是降序的,就称为逆序对
* 返回数组中所有的逆序对
*/
public class Code03_ReverseParis {
private int process (int[] arr, int left, int right)
{
if (left == right) {
return 0;
}
int mid = (left + right)/2;
return process(arr, left, mid) + process(arr, mid + 1, right) + merge(arr, left, mid, right);
}
private int merge (int[] arr, int left,int mid, int right)
{
int[] help = new int[right - left + 1];
int p1 = left;
int p2 = mid +1;
int i = 0;
int result = 0;
while (p1 <= mid && p2 <= right) {
result += arr[p1] < arr[p2] ? 0 : (right - p2 + 1);
//降序
help[i++] = arr[p1] < arr[p2] ? arr[p2++] : arr[p1++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= right) {
help[i++] = arr[p2++];
}
for (int j =0; j < help.length; j++) {
arr[left+j] = help[j];
}
return result;
}
public static void main(String[] args) {
Code03_ReverseParis sort = new Code03_ReverseParis();
int[] arr = {3,8,4,1,0};
int num =sort.process(arr, 0, arr.length-1);
System.out.println(num);
}
}
上面2道题只是开胃菜,递归排序的经典写法都是从左到右进行递归。不知道你们发现没有,想要从左到右,找到右侧比自己大的数,得用升序归并。从左到右想要找到比自己小的数,得用降序归并。
思考: 面试题一是最小和,假设数组为 {5,2,3,4,1},而你使用降序,猜猜得到的最小和会是多少?为什么呢?
面试题3 (Hard):在一个数组中,对于每个数num,求有多少个后面的数 * 2 依然<num,求总个数
比如:[3,1,7,0,2]
3的后面有:1,0
1的后面有:0
7的后面有:0,2
0的后面没有
2的后面没有
所以总共有5个
package code2.排序_03;/**
*在一个数组中,
* 对于每个数num,求有多少个后面的数 * 2 依然<num,求总个数
* 比如:[3,1,7,0,2]
* 3的后面有:1,0
* 1的后面有:0
* 7的后面有:0,2
* 0的后面没有
* 2的后面没有
* 所以总共有5个
*
* 本题测试链接 : https://leetcode.com/problems/reverse-pairs/
*/
public class Code04_BiggerThanRightTwice {
public int reversePairs(int[] nums) {
return this.process(nums, 0, nums.length-1);
}
public int process (int[] arr, int left, int right)
{
if (left == right) {
return 0;
}
int mid = (left + right)/2;
return process(arr, left, mid)
+ process(arr, mid + 1, right)
+ merge(arr, left, mid, right);
}
private int merge (int[] arr, int left,int mid, int right)
{
int result = 0;
// 目前囊括进来的数,是从[M+1, windowR)
int windowR = mid + 1;
//第一次,左右两个大概率是一个数,直接比较
//最后一次,左侧和右侧都是有序的。在合并之前进行比较
for (int i = left; i <= mid; i++) {
while (windowR <= right && (long) arr[i] > (long) arr[windowR] * 2) {
windowR++;
}
result += windowR - mid - 1;
}
int[] help = new int[right - left + 1];
int p1 = left;
int p2 = mid +1;
int i = 0;
while (p1 <= mid && p2 <= right) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= right) {
help[i++] = arr[p2++];
}
for (int j =0; j < help.length; j++) {
arr[left+j] = help[j];
}
return result;
}
public static void main(String[] args) {
Code04_BiggerThanRightTwice sort = new Code04_BiggerThanRightTwice();
int[] arr = {3,1,7,0,2};
int num =sort.process(arr, 0, arr.length-1);
System.out.println(num);
}
}
理解不了归并排序,相信这一题会直接懵逼。
面试题4 (Super Hard):题目描述:https://leetcode.cn/problems/count-of-range-sum/ 给定一个数组arr,两个整数lower和upper,返回arr中有多少个子数组的累加和在[lower,upper]范围上。
package unit2.class05;
// 这道题直接在leetcode测评:
// https://leetcode.com/problems/count-of-range-sum/
public class Code01_CountOfRangeSum {
public static int countRangeSum(int[] nums, int lower, int upper) {
if (nums == null || nums.length == 0) {
return 0;
}
long[] sum = new long[nums.length];
sum[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
sum[i] = sum[i - 1] + nums[i];
}
return process(sum, 0, sum.length - 1, lower, upper);
}
public static int process(long[] sum, int L, int R, int lower, int upper) {
if (L == R) {
return sum[L] >= lower && sum[L] <= upper ? 1 : 0;
}
int M = L + ((R - L) >> 1);
return process(sum, L, M, lower, upper) + process(sum, M + 1, R, lower, upper)
+ merge(sum, L, M, R, lower, upper);
}
public static int merge(long[] arr, int L, int M, int R, int lower, int upper) {
int ans = 0;
int windowL = L;
int windowR = L;
// [windowL, windowR)
for (int i = M + 1; i <= R; i++) {
long min = arr[i] - upper;
long max = arr[i] - lower;
//归并排序,左右两侧都是有序的
while (windowR <= M && arr[windowR] <= max) {
windowR++;
}
//归并排序,左右两侧都是有序的
while (windowL <= M && arr[windowL] < min) {
windowL++;
}
ans += windowR - windowL;
}
long[] help = new long[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
return ans;
}
}
这一题属于相当难的,涉及到前缀和相关知识。后续会更新解题思路





