算法7：平衡二叉树（AVLTree）

二叉排序树（BST, Binary Sort Tree）也称二叉查找树（Binary Search Tree）, 或二叉搜索树。

定义：一颗二叉树，满足以下属性：

• 左子树的所有的值小于根节点的值
• 右子树的所有值大于根节点的值
• 左、右子树满足以上两点

  

   

   

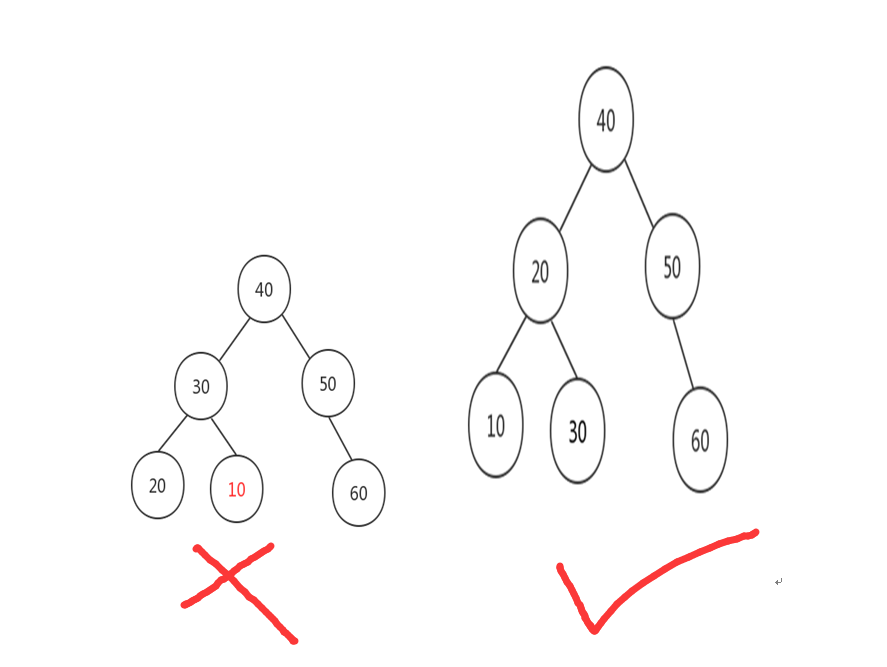
  那么我们如何去构建一个自己的二叉排序树呢？算法实现思路如下：

  

 

　　二叉排序树只是对值进行了排序，但是如果我们对二叉排序树进行树的平衡操作，即对树进行旋转，那么就引出了本文的重要知识点，平衡二叉树（AVL Tree）。《大话数据结构》是这样解释的：

 

 

 

 下面通过几张图片来对AVL树有一个基本的认识：

 

 

 

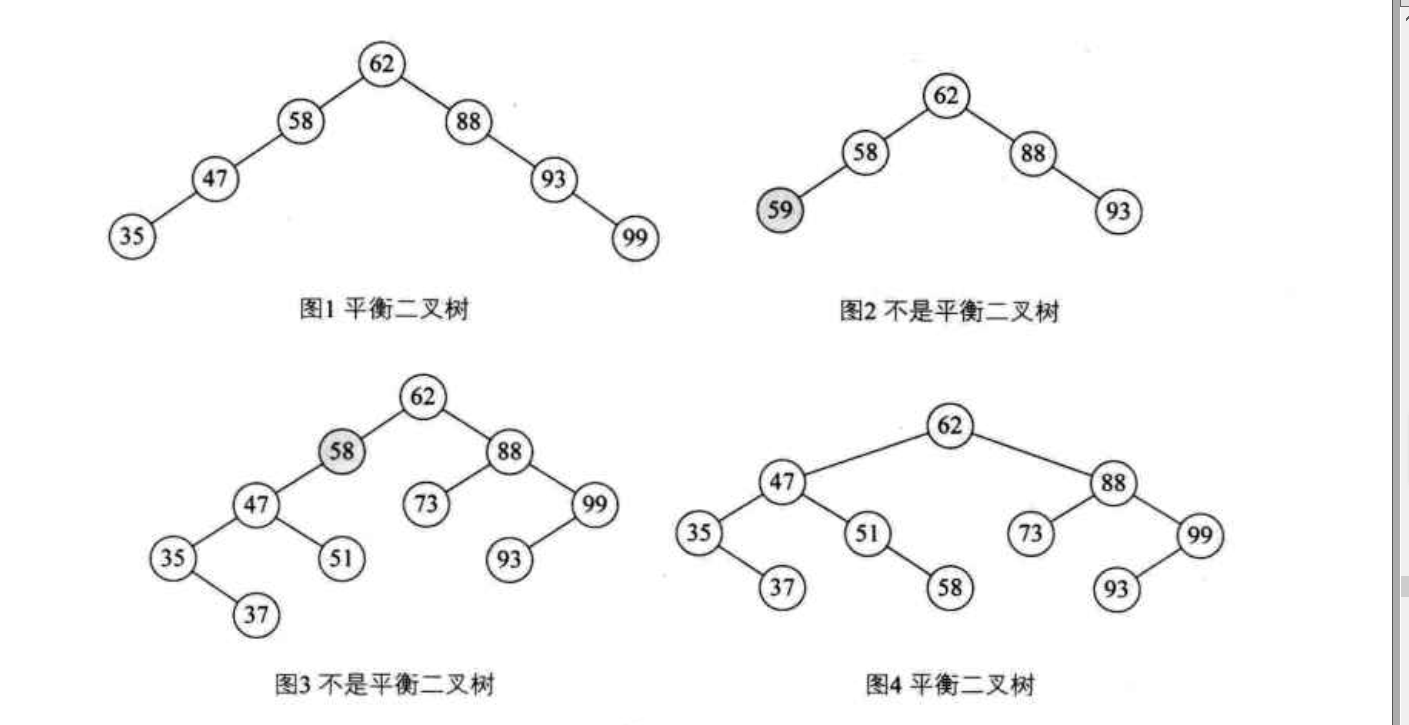
下面通过过右旋，左右旋来做一个简单的介绍。（左旋和右旋相反，左右旋和右左旋相反）

右旋：即对树的根节点重新判定，即左子树最下层的左节点新增节点值，那么可以通过将新生成的根节点往右拉，即可实现平衡。即将新的根节点40拉到旧的根节点50的位置。

 

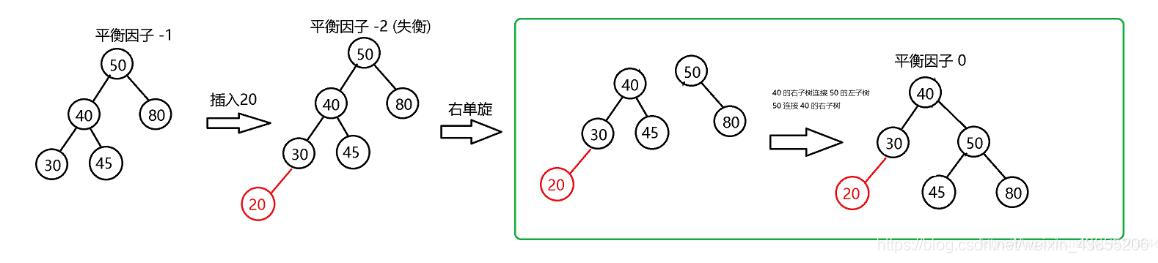
 左右旋：如下图中所展示，先对左子树进行左旋，将原来左子树根节点20变为30，即将30往左拉； 然后再进行右旋，即将整颗树的新的根节点30往右拉

 

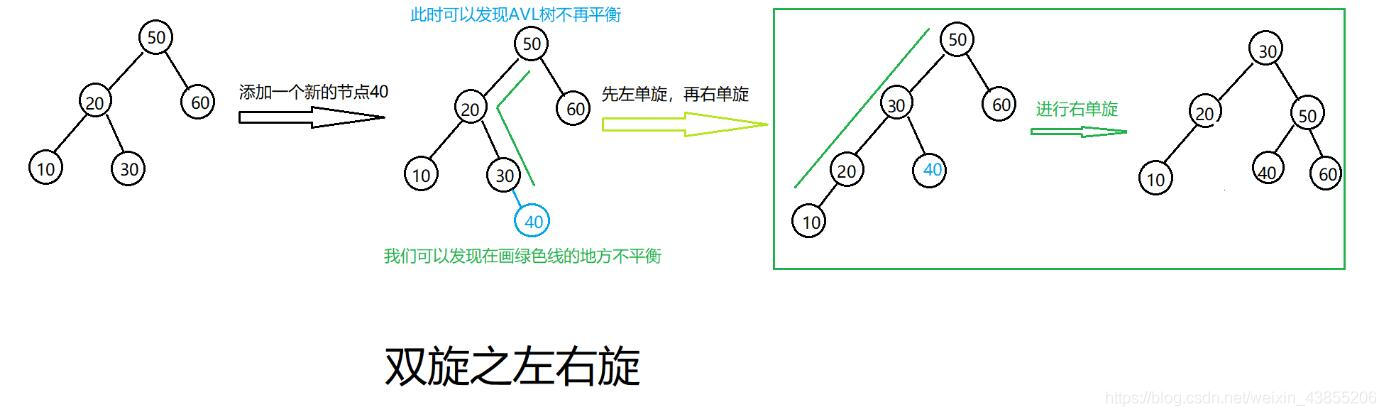
  下面直接接上代码，实现AVL Tree的构造

package code.code_04;

public class AVLTree {
    //节点
    public class Node {
        int data; //数据

        Node left; //左子节点
        Node right;//右子节点
        int height; // 记录该节点所在的高度

        public Node(int data) {
            this.data = data;
            this.height = 1; //只要右节点,那么当前节点的高度就为1.
        }
    }

    public static void printTree(Node root) {
        System.out.println(root.data);
        if(root.left !=null){
            System.out.print("left:");
            printTree(root.left);
        }
        if(root.right !=null){
            System.out.print("right:");
            printTree(root.right);
        }
    }

    //获取节点的高度
    public static int getHeight(Node p){
        return p == null ? 0 : p.height; // 空树的高度为0
    }

    /*
     * 右旋转
     * 右旋示意图(先把30的左节点指向25，然后再将节点20的右节点指向30，即对结点20进行右旋)
     *      30                       20
     *     /  \                     /  \
     *    20  40                  10   30
     *   /  \      --RR旋转-       /   /  \
     *  10   25                  5   25   40
     *  /
     * 5
     *
     */
    public Node RRRotate(Node p) {
        //记录下节点p的左子树，防止树断开
        Node node = p.left;     //失衡点的左子树的根结点20作为新的结点
        p.left = node.right;  //将新节点的右子树25成为失衡点30的左子树，等同于p.left = p.left.right
        node.right = p;         //将失衡点30作为新结点的右子树

        //重新设置失衡点30和新节点20的高度
        p.height = Math.max(getHeight(p.left), getHeight(p.right)) + 1;
        node.height = Math.max(getHeight(node.left), p.height) + 1;
        return node;
    }

    /*
     * LL旋转
     * 左旋示意图(先把20的右节点指向25，然后再将节点30的左节点指向20，即对结点30进行左旋))
     *      20                          30
     *     /  \                        /  \
     *    10  30                     20   40
     *       /  \      --LL旋转-     /  \   \
     *      25  40                 10  25  50
     *           \
     *           50
     *
     */
    public Node LLRotate(Node p){
        //记录下节点p的左子树，防止树断开
        Node node = p.right;     //失衡点的左子树的根结点20作为新的结点
        p.right = node.left;  //将新节点的右子树25成为失衡点30的左子树
        node.left = p;         //将失衡点30作为新结点的右子树

        //重新设置失衡点30和新节点20的高度
        p.height = Math.max(getHeight(p.left), getHeight(p.right)) + 1;
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        return node;
    }

    // LR旋转
    public Node LRRotate(Node p){
        p.left = LLRotate(p.left); // 先将失衡点p的左子树进行RR旋转
        return RRRotate(p); // 再将失衡点p进行LL平衡旋转并返回新节点代替原失衡点p

    }
    // RL平衡旋转
    public Node RLRotate(Node p){
        p.right = RRRotate(p.right); // 先将失衡点p的右子树进行LL平衡旋转
        return LLRotate(p); // 再将失衡点p进行RR平衡旋转并返回新节点代替原失衡点p
    }

    public Node insert(Node root, int data) {
        //如果节点不存在，则直接创建新节点返回，新节点的高度默认为1
        if (root == null) {
            root = new Node(data);
            return root;
        }

        if (data < root.data) {
            //递归一直往下找，直到找到合适的位置为止
            root.left = insert(root.left, data);

            //如果树失衡，则进行平行操作
            if (getHeight(root.left) - getHeight(root.right) > 1) {
                /**
                 * 如果data等于root.left.data，那说明root之前没有左节点。
                 *
                 * 如果data小于root.left.data，那说明data是插入在root.left的子节点中，此时
                 * 我们还需要判断data具体是插入在root.left的左子节点还是右子节点。
                 *
                 * 1.如果是插入root.left的左子节，那么需要进行右旋转
                 * 2.如果是插入root.left的右子节点，那么需要先左旋转，然后再右右（即左右旋转）
                 */
                if (data < root.left.data) { //插入节点在失衡结点的左子树的左边
                    System.out.println("RR旋转");
                    root = RRRotate(root);
                }
                else { //插入节点在失衡结点的左子树的右边
                    System.out.println("左右旋转");
                    root = LRRotate(root);
                }
            }
        }
        else {
            root.right = insert(root.right, data);
            if (getHeight(root.right) - getHeight(root.left) > 1) {
                if(data <= root.right.data){//插入节点在失衡结点的右子树的左边
                    System.out.println("RL旋转");
                    root = RLRotate(root);
                }else{
                    System.out.println("LL旋转");//插入节点在失衡结点的右子树的右边
                    root = LLRotate(root);
                }
            }
        }

        //重新调整root节点的高度值
        root.height = Math.max(getHeight(root.left), getHeight(root.right)) + 1;
        return root;
    }

    public static void main(String[] args) {
        AVLTree tree = new AVLTree();
        Node root = null;

       /* root = tree.insert(root,30);
        root = tree.insert(root,20);
        root = tree.insert(root,40);
        root = tree.insert(root,10);
        root = tree.insert(root,25);*/
        //插入节点在失衡结点的左子树的左边, demo逐个放开验证
        //root = tree.insert(root,5);   //右旋 demo1
        //root = tree.insert(root,15);  //右旋 demo2
        //root = tree.insert(root,24);  //左右旋 demo3
        //root = tree.insert(root,26); //左右旋 demo4

        //测试左旋，右左旋
        root = tree.insert(root,20);
        root = tree.insert(root,10);
        root = tree.insert(root,30);
        root = tree.insert(root,25);
        root = tree.insert(root,40);
        //root = tree.insert(root,39);  //左旋 demo5
        //root = tree.insert(root,41);  //左旋  demo6
        //root = tree.insert(root,24);  //右左旋 demo7
        root = tree.insert(root,26);  //右左旋 demo8

        //打印树，按照先打印左子树，再打印右子树的方式
        tree.printTree(root);
    }
}

 

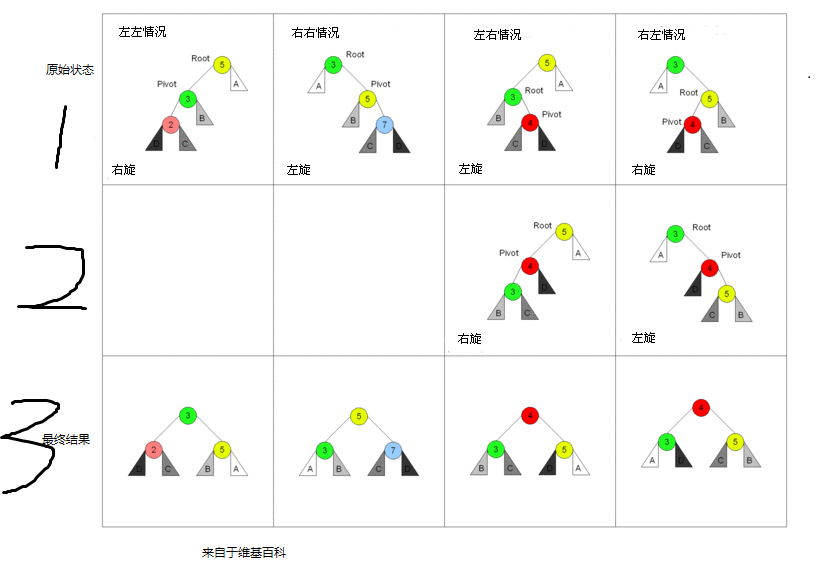
下面通过一张图片，总结一下分别在什么情况下需要左旋，左右旋，右旋，右左旋。 

左旋，右旋只需要一次旋转即可完成树的平衡

左右旋，右左旋需要2次旋转才能完成树的平衡

 

 

 

参考资料：

《大话数据结构》

https://blog.csdn.net/xiaojin21cen/article/details/97602146