算法第五章作业

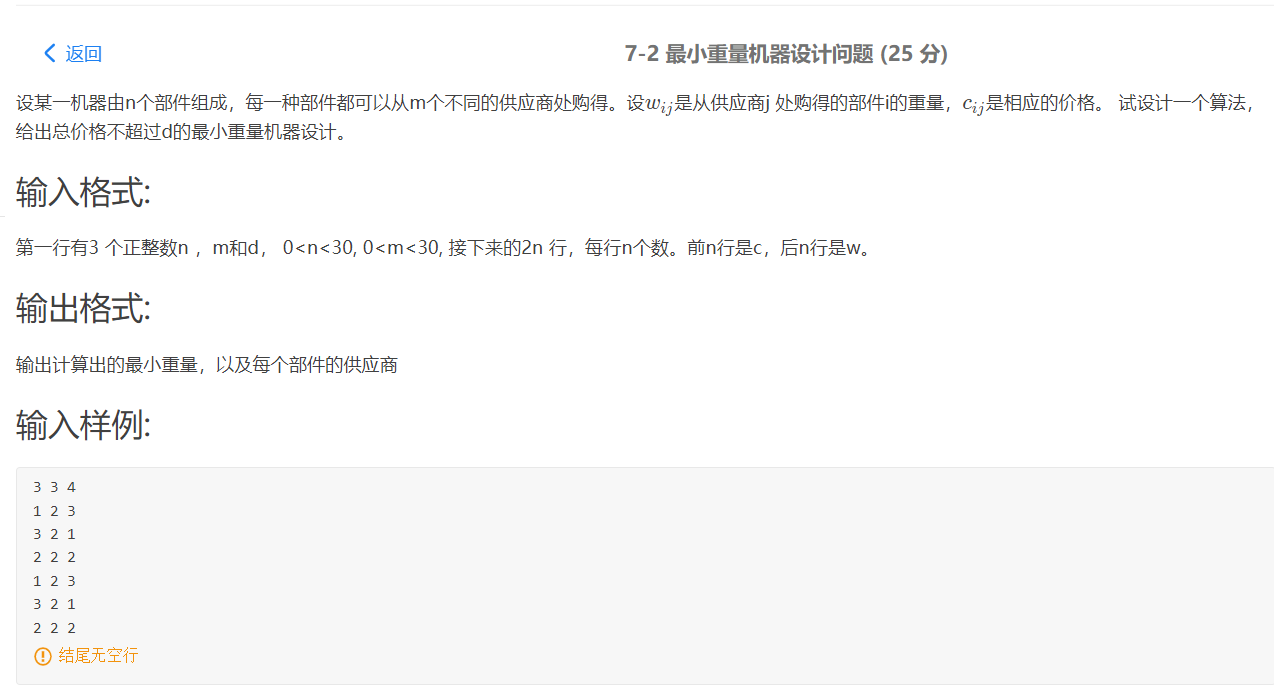
1. 请用回溯法的方法分析“最小重量机器设计问题”

算法描述：

 

 

 

 

代码描述：

 #include <bits/stdc++.h>

using namespace std;

int n,m,d;

int w[40][40];

int c[40][40];

int x[40],X[40];

int minw=100000;

int weight;

int dsum=0;

 

void backtrack(int t){

 if(t>n){

  if(weight<minw){

   minw=weight;

   for(int i=1;i<=n;i++){

    X[i]=x[i];

   }

  }   

  return;

 }

 else{

   for(int i=1;i<=m;i++){

    if(dsum+c[t][i]<=d&&weight+w[t][i]<minw){

     x[t]=i;

     weight+=w[t][i];

           dsum+=c[t][i];   

        backtrack(t+1);

           weight-=w[t][i];

           dsum-=c[t][i];     

    }   

  }

  }

 }

int main(){

 cin>>n>>m>>d;

 for(int i=1;i<=n;i++){

  for(int j=1;j<=m;j++){

   cin>>c[i][j];

  }

 }

 for(int i=1;i<=n;i++){

  for(int j=1;j<=m;j++){

   cin>>w[i][j];

  }

 }

 backtrack(1);

 cout<<minw<<endl;

 for(int i=1;i<=n;i++){

  cout<<X[i]<<" ";

 }

}

1.1 说明“最小重量机器设计问题"的解空间

解空间即进行穷举的搜索空间，包含所有的可能解，这里以样例为例写出解空间：

（i，j，k）表示第1个部件选择第i个供应商，第2个部件选择第j个供应商，第3个部件选择第k个供应商，以此类推。

（1，1，1）（1，1，2）（1，1，3）

（1，2，1）（1，2，2）（1，2，3）

（1，3，1）（1，3，2）（1，3，3）

（2，1，1）（2，1，2）（2，1，3）

（2，2，1）（2，2，2）（2，2，3）

（2，3，1）（2，3，2）（2，3，3）

（3，1，1）（3，1，2）（3，1，3）

（3，2，1）（3，2，2）（3，2，3）

（3，3，1）（3，3，2）（3，3，3）

 

 

1.2 说明 “最小重量机器设计问题"的解空间树

 

 

 

 

1.3 在遍历解空间树的过程中，每个结点的状态值是什么。

每个结点的状态值是该点的重量w和价格c。

2. 你对回溯算法的理解

应用回溯算法的三个步骤：

1.首先得构造解空间树：子集树和排列树；

2.以深度优先的方式搜索解空间：递归或迭代；

3.设计剪枝函数避免无效搜索：使用约束函数，剪去不满足约束条件的路径或使用限界函数，剪去不能得到最优解的路径。

回溯法解问题的一个显著特征是，解空间树是虚拟的，在任何时候，只需保存从根节点到当前扩展结点的路径。

在回溯问题中，若要求问题的所有解，就要回溯到根。