算法第三章上机实验报告
1.1 问题描述
题目名称:
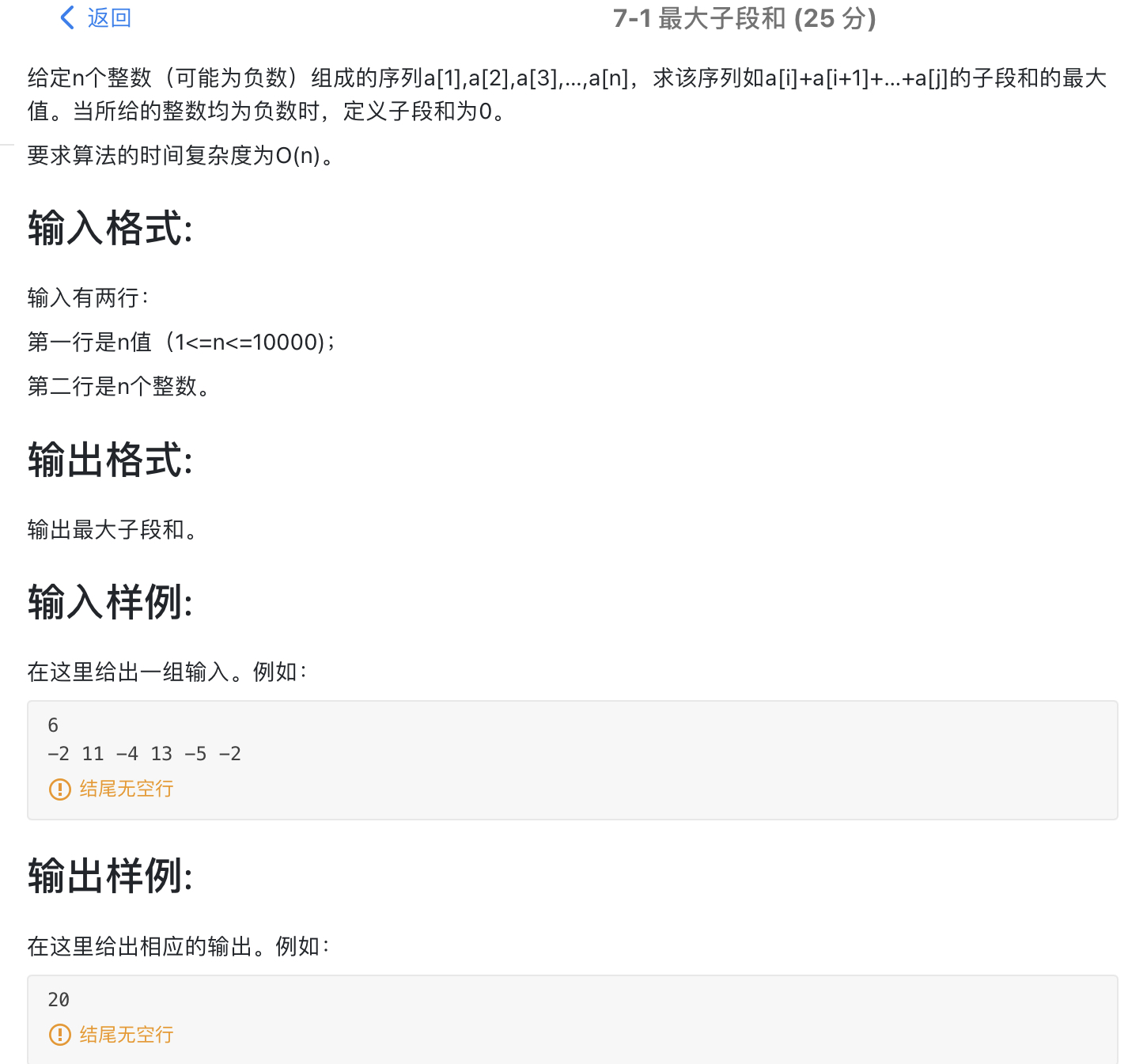
问题描述:给出一组序列,求其连续的一段子序列加起来的和最大,即最大子段和问题。
1.2 算法描述
(1)因为题目要求算法的时间复杂度为o(n),蛮力枚举法O(n^3),优化枚举法O(n^2)分而治之法O(nlogn)都不可以,因此我们考虑用到动态规划。
(2)
给出问题表示:Di:以X[i]开头的最大子数组和
明确原始问题:Smax = max{D[i]},1<=i<=n
1.3 问题求解:
1.3.1 根据最优子结构性质,列出递归方程式。
Di:以X[i]开头的最大子数组和
初始化:D[n]=X[n]
①当D[i+1]<0时:D[i]=X[i];
②当D[i+1]>0时: D[i]=X[i]+D[i+1];
1.3.2 给出填表法中表的维度、填表范围和填表顺序。
纬度:一维
填表范围:1~n
填表顺序:从右到左,自底向上
1.3.3 分析该算法的时间和空间复杂度
时间复杂度:O(n)
原因:因为只使用了一个for循环。
空间复杂度:只用了一个一维数组D[n]来记录计算后的数据。
1.3 心得体会(对本次实践收获及疑惑进行总结)
这次实验课主要是关于动态规划的,对于自己来说难度明显加大了很多,拿到问题很难理清思路,也很难建立递推关系,可能自己看视频的时候就不是很理解,也导致后面回答不上老师问的问题。下次实验课前要认真观看视频,理清每一个步骤。



