【数据结构】常用排序算法和查找算法

排序
在以下排序算法中，关键字比较的次数与记录的初始排列次序无关的是简单选择排序/直接选择排序。
插入排序
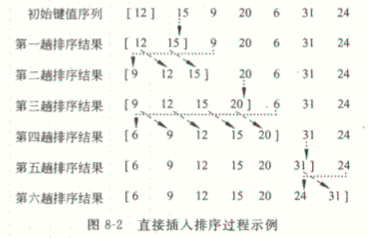
1.直接插入排序
基本思想：依次将待排序序列中的每一个记录插入到一个已排好序的序列中，直到全部记录都排好序。初始数据越接近有序，直接插入排序的效率越高。

void insert_sort(std::vector<int>& r)
{
    int j, tmp;
    for(int i=1; i<r.size(); i++)
    {
        tmp = r[i];
        j = i;
        while(j>0 && tmp<r[j-1])
        {
            r[j] = r[j-1];
            j--;
        }
        r[j] = tmp;
    }
}

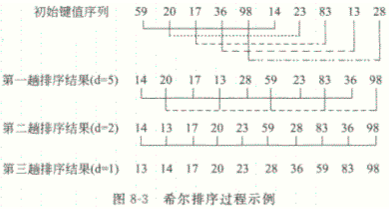
2.希尔排序
基本思想：先将整个待排序记录序列分割成若干个子序列，在子序列内分别进行直接插入排序，待整个序列基本有序时，再对全体记录进行一次直接插入排序。

void shell_sort(vector<int>& v)
{
    int tmp, d=v.size()/2;
    while (d)
    {
        for(int i = d; i < v.size(); i++)
        {
            int j;
            tmp = v[i];
            for(j=i; j>=d; j-=d)
            {
                if(tmp < v[j-d])
                    v[j] = v[j-d];
                else
                    break;
            }
            v[j] = tmp;
        }
        d = int(d/2);
    }
}

交换排序
3.冒泡排序
基本思想：两两比较相邻记录的关键码，如果反序则交换，直到没有反序的记录为止。对n个数据元素最多需要n-1趟冒泡。

void bubble_sort(vector<int>& v)
{
    int i = 1;
    bool finish = false;
    while (i < v.size() && !finish)
    {
        finish = true;
        for(int j=0; j<v.size()-i; j++)
            if(v[j] > v[j+1])
            {
                swap(v[j], v[j+1]);
                finish = false;
            }
        i++;
    }
}

4.快速排序
基本思想：任取一个数据元素作为基准（例如取第一个），按照该数据元素的关键字大小，将整个排序表划分为左右两个子表：左侧字表中所有数据元素的关键字都小于或等于基准数据元素的关键字，右侧子表中所有数据元素的关键字都大于基准数据元素的关键字，基准数据元素则排在这两个子表中间（这也是该数据元素最终应该安放的位置），然后分别对这两个子表重复施行上述方法的快速排序，直到所有的子表长度为1，则排序结束。排序复杂度与元素的初始顺序有关。

 

void quick_sort(int s[], int l, int r)
{
    if (l < r)
    {
        //Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
                j--;  
            if(i < j) 
                s[i++] = s[j];
            
            while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
                i++;  
            if(i < j) 
                s[j--] = s[i];
        }
        s[i] = x;
        quick_sort(s, l, i - 1); // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

 

选择排序
5.简单选择排序
基本思想：第i趟排序在待排序序列r[i]~r[n](1<=i<=n-1)中选取关键码最小的记录，并和第i个记录交换作为有序序列的第i个记录。　

void select_sort(vector<int>& v)
{
     int _min;
     int minIdx;
    for(int i=0; i<v.size()-1; i++)
    {
        int j = i+1;
        _min = v[j];
        minIdx = j; 
        for(; j<v.size(); j++)
            if(v[j] < _min)
            {
                _min = v[j];
                minIdx = j;
            }
        swap(v[i], v[minIdx]);
    }
}

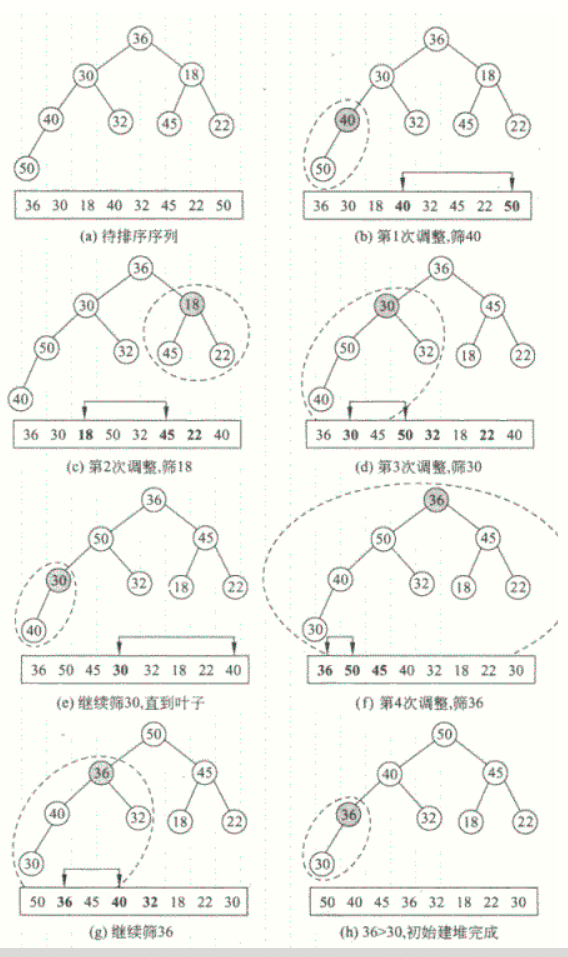
6.堆排序

 

 

// 参考 https://www.jianshu.com/p/d02bb01e9045
void construct_heap(vector<int>&v, int k, int N) 
{
    while(1)
    {
        int i = 2 * k;
        if(i > N)     // 保证该节点是非叶子节点
            break; 

        if(i<N && v[i+1] >v[i]) //选择较大的子节点
            i++;

        if(v[k] >= v[i])    //没下沉到底就构造好堆了
            break;

        swap(v[k], v[i]);
        k = i;  
    }
}

 

 

//堆排序
//父节点元素大于子节点元素
//左子节点角标为2*k
//右子节点角标为2*k+1
//父节点角标为k=N=v.size-1
void heap_sort(vector<int>& v)
{
    int k, N=v.size()-1;

    //构造堆
    //如果给两个已构造好的堆添加一个共同父节点，
    //将新添加的节点作一次下沉将构造一个新堆，
    //由于叶子节点都可看作一个构造好的堆，所以
    //可以从最后一个非叶子节点开始下沉，直至
    //根节点，最后一个非叶子节点是最后一个叶子
    //节点的父节点，角标为N/2
    for(k = N/2; k>=0; k--)
        construct_heap(v, k, N);
    //下沉排序
    while (N > 0)
    {
        swap(v[0], v[N--]);
        construct_heap(v, 0, N);   //将大的放在数组后面，升序排序
    }
        
}

查找
二分查找
二分查找可转换为二叉搜索树，树的深度logN + 1，其平均时间复杂度近似为logN，当二叉搜索树退化为链表时，时间复杂度为O(n),违背了二叉搜索树的二分查找提升效率的初衷，因此引入平衡二叉树。

(未完待续)