【优化方法】牛顿法实例
0. 前言
上一节中已经介绍了牛顿法的一些原理,在本节中举个具体例子,利用牛顿法求解函数最小值。
1. 例子
求解下列函数最小值:
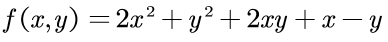
由于这个函数较为简单,所以利用f对x、y分别求偏导数,再令偏导数等于0,就可以求得极值点,又该函数是凸函数(如果分析不出,可视化函数,如下图),所以极值点就是最小值点,故最小值点(-1,1.5).在这里的话,利用牛顿迭代法求解函数最小值。
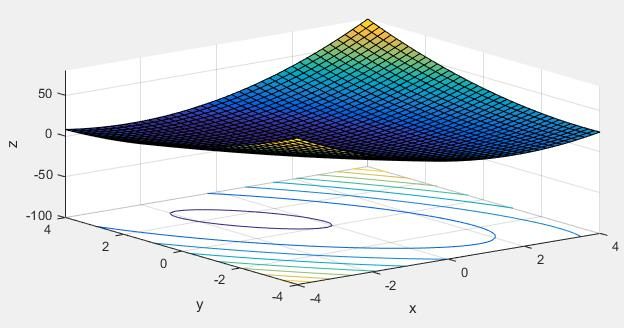
步骤:
![]()
![]()
![]()
![]()
![]()
2. 实施细节
%% 部分参考【1】 % objective function: f(a,b) = 2*a^2 + b^2 + 2*a*b + a - b clear;clc;close A=[4,2;2,2]; x=[2;-2]; tmp=[0;0]; b=[0;0]; delta = 1.0e-8; %前后两次迭代差值 error=1; k=1; max_iters = 10000; history = zeros(max_iters,2); while(k<=max_iters && error > delta) b=[4*x(1,1)+2*x(2,1)+1;2*x(2,1)+2*x(1,1)-1]; tmp=x - inv(A)*b; error=norm(x-tmp,2); x=tmp; history(k,1) = x(1); history(k,2) = x(2); k = k + 1; end x1=x(1,1); x2=x(2,1); f=2*x1*x1+x2*x2+2*x1*x2+x1-x2; fprintf('a=%f,b=%f,f=%f,k=%f',x1,x2,f,k-1); %% 绘图 [X,Y] = meshgrid(-4:.2:4); % 产生网格数据X和Y len = size(X); Z = 2.* power(X,2) + power(Y,2) + 2* X.*Y + X - Y; [DX,DY] = gradient(Z,0.2,0.2); % 计算曲面上各点处的梯度 subplot(2,2,1); surfc(X,Y,Z) xlabel('x');ylabel('y');zlabel('z'); hold on; subplot(2,2,2); contour(X,Y,Z,50) ; % 绘制等高线 title('等高线') subplot(2,2,3); quiver(X,Y,DX,DY); % 绘制梯度场 title('梯度场') subplot(2,2,4); contour(X,Y,Z,50) ; % 绘制等高线 hold on; quiver(X,Y,DX,DY) ; % 绘制梯度场 title('梯度场 + 等高线') xlabel('x'); ylabel('y'); h = get(gca,'Children'); % 获取当前axes对象的所有子对象的句柄 set(h, 'Color','k'); % 设置当前axes对象的所有子对象的颜色为黑色 %% 绘制牛顿法迭代轨迹 x0 = [2,-2]; track = [x0; history]; hold on; subplot(2,2,4); plot(track(1:3,1),track(1:3,2),'rx','markersize',5,'linewidth',1); plot(track(1:3,1),track(1:3,2),'b--','markersize',1,'linewidth',1);
结果:
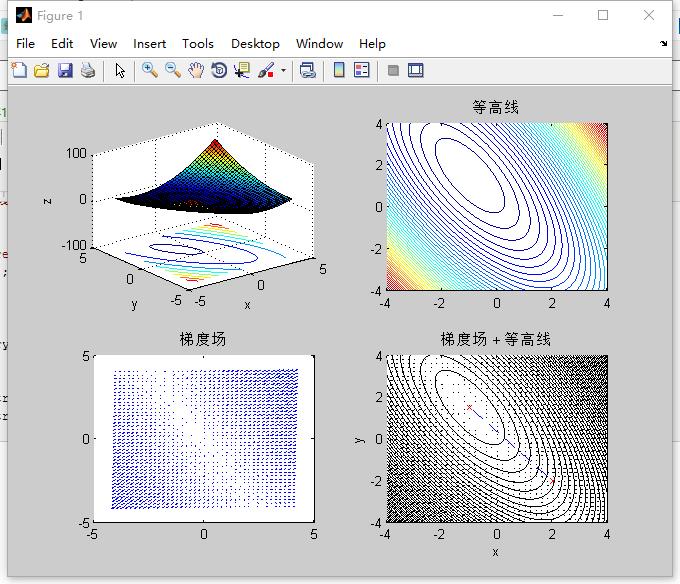
a=-1.000000,b=1.500000,f=-1.250000,k=2.000000>>
参考文献
【1】 https://zhidao.baidu.com/question/198040354.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号