图论7-差分约束系统
抱歉图论两天没更了,今天更一个差分约束,这也是比较有用的一个知识点吧。
差分约束系统是什么呢?给定一些约束条件,然后求出有/没有符合这个约束条件的对其中每个元素的取值,当然,也能算具体的值是多少。
对了,看这篇博客之前先学会SPFA算法。一道例题:luoguP1993
题目大意:有n个变量和一些关系条件,每一种关系条件都形如以下:a>=b+x,a<=b+x或a=b,x是个常数,问这些关系条件是否有矛盾。
差分约束解析:差分约束中的约束条件就是和这道题的条件的形式一样,比如a>=b+x,看到这个,有没有想起SPFA中更新dis[y]是的式子
dis[y]<=dis[x]+val[i]?如果有a<=b+x是不是就能建一个从b到a的路径,权值为x,然后跑最短路就行了。如果建边的那块没有看懂也没事
可以看下面那张图片,清楚的解释了差分约束系统的建边。
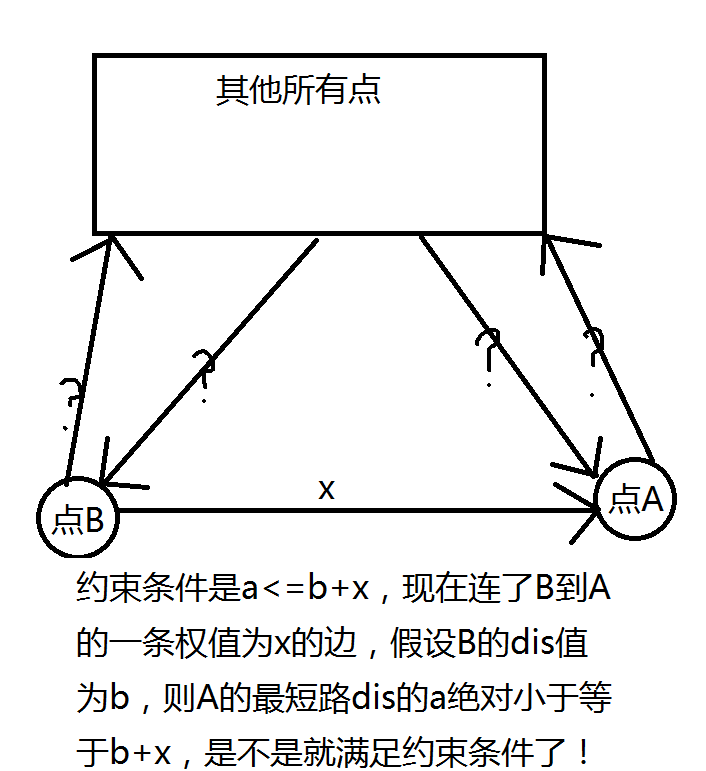
看完这个图之后应该就明白了差分约束的建边原理了,但是还有一类边a>=b+x怎么建呢?很好办,做一个数学转化,变成b<=a+(-x),
是不是现在会建了?就建一条从b到a长度为-x的边就行了。但是这道题中的判断是否成立却有一点难度,怎么叫不成立呢?是不是就是
先说a>=b+x再说a<=b+y且y<x,再看最短路中,就是先建了a->b,-x再建b->a,y,又因为y<x,所以y-x<0所以这种情况就会出现负环
还有几种不成立都会导致负环的产生,所以可以用spfa判一波负环,如果有负环,输出NO,否则输出YES。代码如下:
#include<bits/stdc++.h> #define xms cte #define int long long using namespace std; const int NR=10005; const int INF=1e18+10; int n,m,s; int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*f; } int to[NR*3],nxt[NR*3],val[NR*3]; int head[NR]; int tot=1; void add(int x,int y,int z) { to[tot]=y; val[tot]=z; nxt[tot]=head[x]; head[x]=tot++; } bool flag=0; int dis[NR],cnt[NR]; int cnt2[NR]; bool vis[NR]; void SPFA() { for(int i=0;i<=n;i++) dis[i]=-1e18; queue<int> q; q.push(s); vis[s]=1,dis[s]=0; while(!q.empty()) { int x=q.front(); q.pop(); // cout<<x<<endl; cnt2[x]++; vis[x]=0; if(cnt2[x]>=n) { flag=1; return; } for(int i=head[x];i;i=nxt[i]) { int y=to[i]; if(dis[y]<dis[x]+val[i]) { dis[y]=dis[x]+val[i]; if(!vis[y]) { q.push(y); vis[y]=1; } } } } } signed main() { // freopen("farm.in","r",stdin); // freopen("farm.out","w",stdout); n=read(),m=read(); for(int i=1;i<=m;i++) { int op; op=read(); if(op==1) { int a=read(),b=read(),c=read(); add(a,b,c); } if(op==2) { int a=read(),b=read(),c=read(); add(b,a,-c); } if(op==3) { int a=read(),b=read(); add(a,b,0); add(b,a,0); } } for(int i=1;i<=n;i++) add(0,i,0); SPFA(); if(!flag) puts("Yes"); else puts("No"); return 0; }
注意在洛谷上提交时必须开O2优化,否则洛谷卡bfs版的spfa
然后,基础的差分约束讲完了,现在来讲一些进阶的。
如果发现这个约束条件没有那么容易怎么办呢?下面我来推荐一道题:POJ1275
题目大意:有一家24小时超市,每个小时最少需要a[i]个员工,有n(n<=1000)个应聘者,每个人都有一个参数x,表示从第x之后8个小时,
这个人能工作,问招聘多少人能满足要求。如果不能满足,则输出No solution。
题目解析:这道题如果不说是差分约束是不是很那想到啊?这道题怎么差分约束呢?首先要确定节点是什么,然后再想别的。我们用s数组
表示前缀和,s[i]表示所有i天之前工作者的数量,易得s[i]-s[i-8]>=a[i],但当i<7时,就会涉及三元不等式,为了解决这个问题,我们可以
枚s[23],并将i<7时变成二元不等式,然后做spfa就行了。建议大家先不看代码,自己写一写这道题。
但我还是将代码放在这里吧
#include<bits/stdc++.h>
using namespace std;
const int NR=105;
const int MR=2e3+10;
int n;
int a[NR],num[NR];
int to[MR],nxt[MR],val[MR];
int head[NR];
int tot=1;
void add(int x,int y,int z)
{
to[tot]=y;
val[tot]=z;
nxt[tot]=head[x];
head[x]=tot++;
}
int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch<='9'&&ch>='0'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
bool vis[NR];
int dis[NR];
void Init()
{
tot=1;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(dis,-0x3f,sizeof(dis));
}
void build(int x)
{
for(int i=0;i<=23;i++)
{
add(i,i+1,0);
add(i+1,i,-num[i]);
}
for(int i=7;i<=23;i++) add(i-7,i+1,a[i]);
add(0,24,x),add(24,0,-x);
for(int i=0;i<=6;i++) add(i+17,i+1,a[i]-x);
}
bool check(int x)
{
Init();
build(x);
queue<int> q;
q.push(0),dis[0]=0,vis[0]=1;
while(!q.empty())
{
int now=q.front();q.pop();vis[now]=0;
if(now==24&&dis[now]>x) return 0;
for(int i=head[now];i;i=nxt[i])
{
int y=to[i];
if(dis[y]<dis[now]+val[i])
{
dis[y]=dis[now]+val[i];
if(!vis[y])
{
q.push(y);
vis[y]=1;
}
}
}
}
return dis[24]==x;
}
void solve()
{
int ans=-1;
for(int i=0;i<=n;i++)
{
if(check(i))
{
ans=i;
break;
}
}
if(ans<0) puts("No Solution");
else printf("%d\n",ans);
}
int main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
int T=read();
while(T--)
{
memset(num,0,sizeof(num));
for(int i=0;i<=23;i++)
{
a[i]=read();
}
n=read();
for(int i=1;i<=n;i++)
{
int x=read();
num[x]++;
}
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号