l'Hopital法则

     l'Hopital法则是我们求极限时的利器。当我们一般的代入法得到一个形如0/0或者∞/∞的无法求取的极限时，l'Hopital法则几乎是万能的，当然，也仅限于0/0型和∞/∞的极限。然而l'Hopital法则的威力如果配合我们的机智是十分强大的，因为许多无法通过代入法求得的极限都可以化成可以解决的形式。

     关于l'Hopital法则的证明实际上是很简单的。它的形式为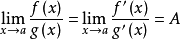，当f（a）=g（a）=0的时候，f（x）和g（x）在a附近都趋近于0，我们在分式上下同时除以x-a，显然分式并没有改变，x-a是一个趋近于0的量，根据导数的定义可以得到上述等式中间的式子。

     l‘Hopital法则的直接应用其实很容易上手，比如极限lim（x→0）【x/sinx】，是一个0/0型的极限，对分式上下同时求导，得到它等于lim（x→0）【1/cosx】，这时我们就可以用代入法得到极限的值为1。这个极限在工程上是有用的，比如单摆摆动的问题，我们一般说单摆的摆动在角度不太大的时候是一个谐振动，其根据就是这个极限：在角度θ接近于0的时候，可以用θ代替sinθ，这时摆球受力是线性的，如果角度太大，θ偏离sinθ太多，这时摆球受力就不是线性的了，其运动也就不是谐振动了。

     关于形如0·∞的极限，可以把它变成0除以1/∞的形式，也就是0/0。另一个非常常见的例子是一个1^∞的极限。lim（x→∞）【1+1/x】^x=e，这个极限是通过求ln【1+1/x】^x的极限得到的，ln【1+1/x】^x又可以化成xln【1+1/x】，这就是一个0·∞的极限，读者可以自己尝试证明它。

     总结：对于一个不能直接求出来的极限，把它化成0/0或∞/∞的形式再运用l’Hopital法则将给你带来惊喜。