题解 P4809 [CCC2018] 最大战略储备

link

最无聊的时候写的最啰嗦详细的题解。

---

题目描述

给定一个 $n\times m$ 的点阵和两类边，第 $i$ 行 $j$ 列的城市我们叫祂城市 $(i,j)$。

横边：给定 $p$ 个三元组 $(u_i,v_i,w_i)$，表示 对于 $a=1,2,\dots ,n$，城市 $(a,u_i)$ 和 $(a,v_i)$ 之间有一条权为 $w_i$ 的边。

纵边：给定 $q$ 个三元组 $(x_i,y_i,z_i)$，表示 对于 $b=1,2,\dots ,n$，城市 $(x_i,b)$ 和 $(y_i,b)$ 之间有一条权为 $z_i$ 的边。

在保持全部点联通的前提下删去一些边，问删去边权值和最大是多少。

$n,m,p,q\le {10}^5$

---

题目解法

首先「最大化删除边权和」相当于「最小化剩余边权和」，后者是最小生成树。暴力的，我们可以建出所有的点和边去跑 Kruskal，边数 $g=np+mq$，这样子复杂度是爆炸的 $O(g\log g+g\alpha (g))$。

我们观察到这玩意复杂度在排序的地方很瓶颈，考虑到很多边形式相同，我们可以不先展开 $a,b$ 再排序，而是先排序规则，Kruskal 的时候再展开，这样复杂度变成了 $O((p+q)\log (p+q)+g\alpha (g))$，已经好很多了，但是还是不够。

我们手玩一下 Kruskal 的过程（嫌麻烦可以直接看 p5（（（

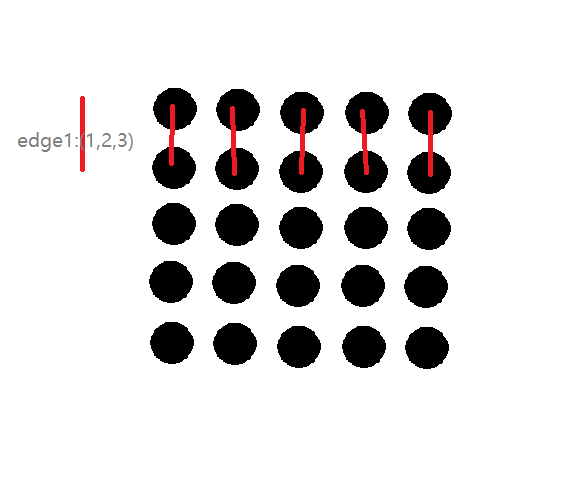
这条边，「大千世界，畅通无阻」。

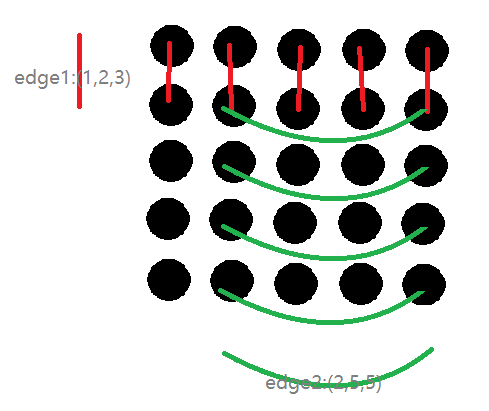
我们发现因为第二行和第二行每一列都联通了，于是乎可以在 $a=1,2$ 中二选一，少连一条边！！！（（（

跟上一步差不多，因为第三行第五行每一列联通，所以 $b=3,5$ 还是二选一 qwq（

发现是 $a=1,2$ 二选一，$a=3,5$ 二选一，加上 $a=4$ 呀 /youl

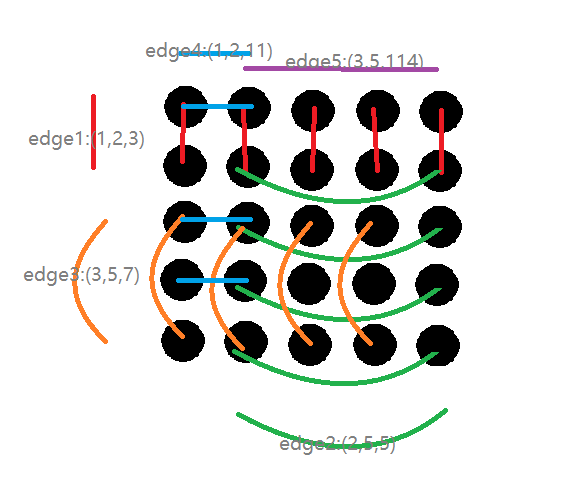
发现这样子本来就是联通的捏，那就不用连啦（（（（（

手玩完了之后，我们发现一个小结论，新加一种边其实就是给每一个联通块（定义是缩行缩列后的那种）加上一条边，意思是设把每列缩成一个点的联通块个数为 $r$，设把每行缩成一个点的联通块个数设为 $c$。横边的话要加 $r$ 条，纵边的话要加 $c$ 条。

假设我们现在选了 $r$ 种横边 $c$ 种纵边，显然 $i=n-r,j=m-c$。然后联通拿普通 dsu 随便维护就可以了。复杂度 $O((p+q)\log (p+q))$。

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N=5e6+10;
int n, m, p, q, tot, fa[N], cl, cr, ans, sum;
struct dat { int op, x, y, w; } a[N];
bool cmp(dat u,dat v) { return u.w<v.w; }

int get(int x) {
	if(fa[x]==x) return x;
	return fa[x]=get(fa[x]); 
}

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n >> m >> p >> q;
	for(int i=1; i<=p; ++i) {
		tot++;
		cin >> a[tot].x >> a[tot].y >> a[tot].w;
		a[tot].op=1, sum+=a[tot].w*n;
	}
	for(int i=1; i<=q; ++i) {
		tot++;
		cin >> a[tot].x >> a[tot].y >> a[tot].w;
		a[tot].op=2, sum+=a[tot].w*m;
	}
	sort(a+1,a+1+tot,cmp);
	for(int i=1; i<=n+m; ++i) fa[i]=i;
	for(int l=1; l<=tot; ++l) {
		if(a[l].op==1) {
			int x=get(a[l].x), y=get(a[l].y);
			if(x^y) fa[x]=y, ans+=a[l].w*(n-cr), cl++;
		}
		else {
			int x=get(a[l].x+m), y=get(a[l].y+m);
			if(x^y) fa[x]=y, ans+=a[l].w*(m-cl), cr++;
		}
	}
	cout << sum-ans;
	return 0;
}