斜率优化DP
前置芝士 单调队列优化 DP
⌈ 写不动数据结构呜呜呜,先来补这个 ⌋
对于一个 DP,我们想优化祂的 ⌈ 转移 ⌋
有些题目的可选状态有以下特征
-
需要寻找最值
-
可选状态区间平移
-
存在可以永久去除的多余状态
感性的讲,可行性是一个滑动窗口,状态两两之间都可以 ⌈ 直接比较出优劣 ⌋ 且 ⌈ 优劣比较可以传递 ⌋
这样就有可能可以单调队列优化力
对于两个状态 \(i,j\) ,如果 \(j\) 比 \(i\) 贡献好,失效晚,那么这个 \(i\) 就没有任何价值,非常的逊,否则 \(i,j\) 都是有可能成为队首滴,一个可以 ⌈ 用实力碾压对手 ⌋ ,一个可以 ⌈ 等对手退役 ⌋
我们维护一个单调的队列,使得队列越前面的选择越优秀,保持队列单调
每次我们做出以下行动
-
去除队首多余状态
-
去除队尾比新状态逊的状态
-
队首即为所求,取用
-
加入新状态
这里要注意的是这些步骤顺序要 ⌈ 结合题目具体考虑 ⌋ 哦 QWQ
斜率优化
tmd 的有点折磨人
我们要考虑 \(j_1,j_2(j_2>j_1)\) 两个决策之间的优劣
先写出 \(j_x->i\) 的贡献,注意如果这里有平方之类的东西我们需要强拆化简掉
之后考虑何时 \(j_2\) 比 \(j_1\) 优,注意参数分离哦
化式子的时候我们要着力于将只含 \(j_1,j_2\) 或者含有 \(j1,j2\) 的三种尽力分来来,为了让状态相对独立 ,然后含有 \(j_x\) 的式子可能有点长,我们用函数代替掉
最后,写成斜率式子,形式类似 \(t(j_1,j_2)=\frac{y(j_1)-y(j_2)}{x(j_1)-x(j_2)}<g(i)\) 啦!
这种左边 ⌈ 两点成斜率 ⌋ 的式子可以使用一种大法: ⌈ 斜率优化 ⌋
注意这里的函数 \(x(i),g(i)\) 要单调哦
我们用 \(j_1,j_2,...,j_k\) 表示队列中的决策哈
那么有两个重要的结论
- \(t(j_r,j_{r+1})<g(i)\) 之类的,反正满足那个式子,且最优决策在队首队尾之类的地方,看题目的单调性具体咋样
大概这样

- 可以维护相邻决策之间的斜率单调减或者增
大概这样

总结一下,大概这样
另外还有一种理解方式,\(g(i)\) 左右对应两种不同答案,一边一种优
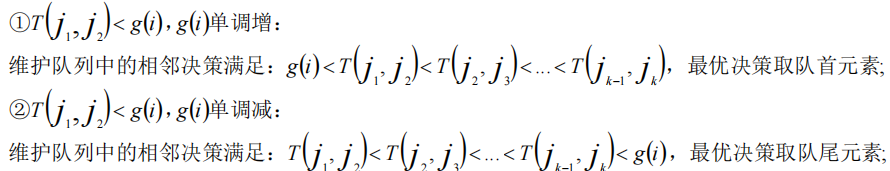
和这样
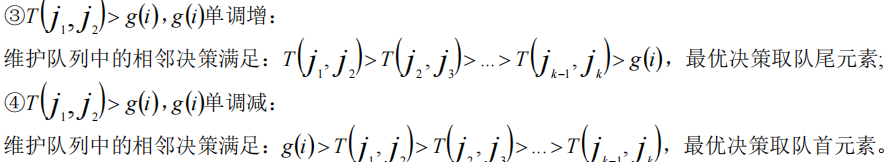
(图片转自 WC2016 课件)
另外,如果 \(g(i)\) 不单调了,可以不弹队列一端,然后二分


