二分专项训练（二分搜索+二分答案的十二道例题及解析
这是一篇关于二分的专项训练，现包括一道二分搜索，十一道二分答案，难度基本上是递增的，持续更新ing
二分搜索
Music Notes
题目描述：
FJ is going to teach his cows how to play a song. The song consists of N (1 <= N <= 50,000) notes, and the i-th note lasts for Bi (1 <= Bi <= 10,000) beats (thus no song is longer than 500,000,000 beats). The cows will begin playing the song at time 0; thus, they will play note 1 from time 0 through just before time B1, note 2 from time B1 through just before time B1 + B2, etc.
However, recently the cows have lost interest in the song, as they feel that it is too long and boring. Thus, to make sure his cows are paying attention, he asks them Q (1 <= Q <= 50,000) questions of the form, "In the interval from time T through just before time T+1, which note should you be playing?" The cows need your help to answer these questions which are supplied as Ti (0 <= Ti <= end_of_song).
Consider this song with three notes of durations 2, 1, and 3 beats:
Beat: 0 1 2 3 4 5 6 ...
|----|----|----|----|----|----|--- ...
1111111111 : :
22222: :
333333333333333:
Here is a set of five queries along with the resulting answer:
Query Note
2 2
3 3
4 3
0 1
1 1
题意：
有n种音符，每种音符叫 i（ 1 <= i <= n )，b[i]表示 i 音符持续的时间，m次询问，问你t[i]时刻放的是什么音符
思路：
二分查找 + 前缀和
对b[i]做一次前缀和，然后对于每次询问，都去前缀和里面二分查找b[i]，输出对应的位置即可
二分可以用lowerbound，也可以手写，这里两种都给出来（实测lower bound比手写快
坑点：
二分查找的时候是去查找t[i] + 1, 找到的pos 最后输出的时候要+1
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll k;
ll n, m, x;
ll pos;
vector<ll>sum;
int main(){
io;
cin>>n>>m;
k = 0;
for(int i = 1; i <= n; ++i){
cin>>x;
k += x;
sum.push_back(k);
}
for(int i = 1; i <= m; ++i){
cin>>x;
pos = lower_bound(sum.begin(), sum.end(),x + 1) - sum.begin();
cout<<pos + 1<<endl;
}
return 0;
}
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
int t, n, m, x;
int sum[MAX];
int lowerbound(int x){
int l = 1, r = n;
while (l <= r) {
int mid = (l + r) / 2;
if(x <= sum[mid])r = mid - 1;
else l = mid + 1;
}
return l - 1;
}
int main(){
cin>>n>>m;
for(int i = 1; i <= n; ++i){
cin>>x;
sum[i] = sum[i - 1] + x;
}
for(int i = 1; i <= m; ++i){
cin>>x;
cout<<lowerbound(x + 1) + 1<<endl;
}
return 0;
}
二分答案
Drying
题目描述：
It is very hard to wash and especially to dry clothes in winter. But Jane is a very smart girl. She is not afraid of this boring process. Jane has decided to use a radiator to make drying faster. But the radiator is small, so it can hold only one thing at a time.
Jane wants to perform drying in the minimal possible time. She asked you to write a program that will calculate the minimal time for a given set of clothes.
There are n clothes Jane has just washed. Each of them took ai water during washing. Every minute the amount of water contained in each thing decreases by one (of course, only if the thing is not completely dry yet). When amount of water contained becomes zero the cloth becomes dry and is ready to be packed.
Every minute Jane can select one thing to dry on the radiator. The radiator is very hot, so the amount of water in this thing decreases by k this minute (but not less than zero — if the thing contains less than k water, the resulting amount of water will be zero).
The task is to minimize the total time of drying by means of using the radiator effectively. The drying process ends when all the clothes are dry.
题意：
n件衣服，每件衣服都有一定的含水量，每分钟每件衣服的含水量会减少1，你有一个吹风机，每分钟只能对一个衣服使用吹风机，且这分钟过完了，衣服的含水量会减少k，问你最少要多少分钟能让所有衣服的含水量非正
思路：
二分的入门题，去二分所需的分钟
二分最重要的就是check函数怎么写，这个题的话，我们计算x分钟时每个衣服需要吹几分钟的吹风机，然后加起来和k比较即可
坑点：
使用吹风机的时候总共让一件衣服的水少k，这个k包含了一分钟内水自然蒸发掉的那个1
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 200000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n, k;
ll tr[MAX];
bool judge(ll t){
ll sum = 0;
for(int i = 1; i <= n; ++i){
if(tr[i] <= t)continue;
else {
sum += (tr[i] - t + k - 2) / (k - 1);
}
}
if(sum > t)return false;
return true;
}
int main(){
io;
n = IntRead();
ll l = 1, r = 0;
for(int i = 1; i <= n; ++i){
tr[i] = IntRead();
r = max(r, tr[i]);
}
k = IntRead();
if(k == 1){
cout<<r<<endl;
}
else {
r = inf;
while (l <= r) {
ll mid = (l + r) / 2;
if(judge(mid))r = mid - 1;
else l = mid + 1;
}
cout<<l<<endl;
}
return 0;
}
P2759 奇怪的函数
题目描述：
使得 \(x^x\)达到或超过 n 位数字的最小正整数 x 是多少？
思路：
显然，这是有单调性滴，可以二分
一看数据2e9，肯定得进行优化，怎么优化呢？
\(x^x >= 10^{n - 1}\)
同时取log即可啊
所有推出来
这就是check的主要内容
剩下的就是套一下板子即可
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 200000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n;
bool check(ll x){
if(x * log10(x * 1.0) >= n - 1)return true;
else return false;
}
int main(){
io;
cin>>n;
ll l = 1, r = inf * 2;
while (l <= r) {
ll mid = (l + r) / 2;
if(check(mid))r = mid - 1;
else l = mid + 1;
}
cout<<l<<endl;
return 0;
}
P1873 砍树
题目描述：
伐木工人米尔科需要砍倒M米长的木材。这是一个对米尔科来说很容易的工作，因为他有一个漂亮的新伐木机，可以像野火一样砍倒森林。不过，米尔科只被允许砍倒单行树木。
米尔科的伐木机工作过程如下：米尔科设置一个高度参数H（米），伐木机升起一个巨大的锯片到高度H，并锯掉所有的树比H高的部分（当然，树木不高于H米的部分保持不变）。米尔科就行到树木被锯下的部分。
例如，如果一行树的高度分别为20，15，10和17，米尔科把锯片升到15米的高度，切割后树木剩下的高度将是15，15，10和15，而米尔科将从第1棵树得到5米，从第4棵树得到2米，共得到7米木材。
米尔科非常关注生态保护，所以他不会砍掉过多的木材。这正是他为什么尽可能高地设定伐木机锯片的原因。帮助米尔科找到伐木机锯片的最大的整数高度H，使得他能得到木材至少为M米。换句话说，如果再升高1米，则他将得不到M米木材。
思路：
砍树的高度是有单调性滴，所有可以去二分它啊
check函数也很简单，这里不过描述
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n, m;
ll tr[MAX];
bool check(ll x){
ll sum = 0;
for(int i = 1; i <= n; ++i){
if(tr[i] > x)sum += (tr[i] - x);
}
if(sum < m)return true;
else return false;
}
int main(){
cin>>n>>m;
for(int i = 1; i <= n; ++i)cin>>tr[i];
ll l = 1, r = inf;
while (l <= r) {
ll mid = (l + r) / 2;
if(check(mid))r = mid - 1;
else l = mid + 1;
}
cout<<l - 1<<endl;
return 0;
}
P1824 进击的奶牛
题目描述
Farmer John建造了一个有N(2<=N<=100,000)个隔间的牛棚，这些隔间分布在一条直线上，坐标是x1,...,xN (0<=xi<=1,000,000,000)。
他的C(2<=C<=N)头牛不满于隔间的位置分布，它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗，Farmer John想把这些牛安置在指定的隔间，所有牛中相邻两头的最近距离越大越好。那么，这个最大的最近距离是多少呢？
思路：
最大的最近距离，很显然是二分
那如何写check函数呢？这里就是个贪心
从头开始放，然后往后找，遇到能放进去的就放进去，最好统计一下放了多少头牛，即可作为返回的判断
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 200000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
int n, c;
int tr[MAX];
bool judge(int x){
int last = tr[1];
int cnt = 1;
for(int i = 2; i <= n; ++i){
if(tr[i] - last >= x){
last = tr[i];
++cnt;
}
}
if(cnt >= c)return true;
return false;
}
int main(){
io;
cin>>n>>c;
for(int i = 1; i <= n; ++i)cin>>tr[i];
sort(tr + 1, tr + 1 + n);
int l = 1, r = inf;
while (l <= r) {
int mid = (l + r) / 2;
if(judge(mid))l = mid + 1;
else r = mid - 1;
}
cout<<l - 1<<endl;
return 0;
}
P2678 [NOIP2015 提高组] 跳石头
二分答案的进阶版
题目描述：
这项比赛将在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有 N块岩石（不含起点和终点的岩石）。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。
为了提高比赛难度，组委会计划移走一些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走 M块岩石（不能移走起点和终点的岩石）。
思路：
问的是最短跳跃距离的最大值，所以就去二分最短跳跃距离即可
对于check函数，我们可以先根据岩石的位置，得到岩石与岩石之间的距离，然后对于枚举的x，去看需要拆多少个石头才能保证最短距离大于等于x，用这个和m进行比较，来确定是返回true还是false
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 200000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n, L, m, len, last, now;
ll tr[MAX];
bool check(ll x){
ll cnt = 0, sum = 0;
for(int i = 1; i <= len; ++i){
if(sum + tr[i] >= x){
sum = 0;
}
else {
++cnt;
sum += tr[i];
}
}
if(cnt <= m)return true;
else return false;
}
int main(){
cin>>L>>n>>m;
for(int i = 1; i <= n; ++i){
cin>>now;
tr[++len] = now - last;
last = now;
}
tr[++len] = L - last;
ll l = 1, r = inf;
while (l <= r) {
ll mid = (l + r) / 2;
if(check(mid)) l = mid + 1;
else r = mid - 1;
}
cout<<l - 1<<endl;
return 0;
}
P1182 数列分段 Section II
题目描述：
在这里插入图片描述
思路：
问的是每段和都最大值最小为多少
所以可以去二分每段和的最大值
因为必须得是连续的才能分到一组，所以就可以去看看每段和的最大值为x时能分几组，然后和m进行比较，得到返回值
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 200000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n, m;
ll tr[MAX];
bool judge(ll x){
ll sum = 0, cnt = 0;
for(int i = 1; i <= n; ++i){
if(tr[i] > x)return false;
if(sum + tr[i] <= x){
sum += tr[i];
if(i == n)++cnt;
}
else {
sum = tr[i];
++cnt;
}
}
if(cnt <= m)return true;
else return false;
}
int main(){
cin>>n>>m;
for(int i = 1; i <= n; ++i)cin>>tr[i];
ll l = 1, r = inf;
while (l <= r) {
ll mid = (l + r) / 2;
if(!judge(mid))l = mid + 1;
else r = mid - 1;
}
cout<<l<<endl;
return 0;
}
P1024 [NOIP2001 提高组] 一元三次方程求解
题目描述
思路：
某谷的大佬们都tm什么神仙解法：盛金公式？牛顿迭代法？勘根定理？卡尔丹公式？割线法？暴力求导+分类讨论？线性求解？还有直接枚举1e5秒过的 orzzzz，真神了
这题其实和一次函数求零点一样，去二分答案，不过这次是有三个解，就不能像平时那样去二分了，再看根的范围是[-100, 100]，同时根的差的绝对值 不小于1，由此，我们可以对[-100, 100]内200个长度为1的区间进行二分答案，复杂度为$$n*\log_2{n}，$$
但是比较坑的就是，枚举到 i 时发现i是答案的情况要注意，因为你可能会写输出重复了，因为在[i - 1, i]的时候输出了一次，在[i, i + 1]的时候又输出了一次，所以就有问题……
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
double a, b, c, d;
double l, r;
double ans;
double cal(double x){//算函数值
double k = a * x * x * x + b * x * x + c * x + d ;
return k;
}
int main(){
cin>>a>>b>>c>>d;
for(int i = -100; i <= 99; ++i){//美剧区间起点
l = i; r = i + 1;
if(cal(l) == 0)printf("%.2lf ", l);
if(cal(l) * cal(r) >= 0)continue;
while (r - l >= 0.001) {
double mid = (l + r) / 2;
if(cal(l) * cal(mid) <= 0)r = mid;
else l = mid;
}
printf("%.2lf ", l);
}
return 0;
}
Chocolate Eating
题目描述：
Bessie has received N (1 <= N <= 50,000) chocolates from the bulls, but doesn't want to eat them too quickly, so she wants to plan out her chocolate eating schedule for the next D (1 <= D <= 50,000) days in order to maximize her minimum happiness level over the set of those days.
Bessie's happiness level is an integer that starts at 0 and halves (rounding down if necessary) over night as she sleeps. However, when she eats chocolate i, her happiness level increases by integer HiH_iHi (1 <= HiH_iHi <= 1,000,000). If she eats chocolates on a day, her happiness for that day is considered the happiness level after she eats the chocolates. Bessie insists that she eat the chocolates in the order that she received them.
If more than one optimal solution exists, print any one of them.
Consider a sequence of 5 chocolates to be eaten over a period of 5 days; they respectively bring happiness (10, 40, 13, 22, 7).
If Bessie eats the first chocolate (10 happiness) on the first day and then waits to eat the others, her happiness level is 10 after the first day.
题意：
贝西从bulls那里收到了N块巧克力。
她不想把它们马上吃完，而是打算制定一个计划，使得在接下来的D天里，使得每天的最小快乐值最大。
贝西的快乐指数可以用一个整数来衡量，一开始的时候是0，当她每天晚上睡觉的时候，快乐指数会减半（奇数时向下取整）。贝西把她的巧克力按照收到的时间排序，并坚持按照这个顺序来吃巧克力。当她吃掉第i块巧克力的时候，她的快乐指数会增加Hj。她那天的快乐值被认为是她吃完巧克力后的快乐水平。每天可以吃任意多块巧克力，如何帮助贝西合理安排，使得D天内她的最小快乐指数最大呢？
思路：
很明显，最小的快乐值最大，得二分
所以我们去二分最小快乐值
最后需要再check一下答案，来记录吃巧克力的天数
那么如何写check函数？
就用循环去跑天数，用sum记录快乐值，如果这一天的sum小于x，就循环去加上接下来的快乐值，直到sum > x时 ，就可以结束这一天，也就是让sum/2。如果len > n，也就是快乐都加没了他还不满足此时的x，就说明快乐值太大了，所吃的不能满足，就得往左缩缩，反之如果全跑完都没问题，就得往右缩缩
坑点！！！
巧克力要全部吃完！
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll n, m, len, k, sum;
ll ans[MAX];
ll tr[MAX];
bool check(ll x){
len = 0;sum = 0;
for(int i = 1; i <= m; ++i){
while (sum < x) {
sum += tr[++len];
if(len > n)return false;
if(x == k)ans[len] = i;
}
sum /= 2;
}
return true;
}
int main(){
n = IntRead(); m = IntRead();
for(int i = 1; i <= n; ++i)tr[i] = IntRead();
ll l = 1, r = 1e12;
while (l <= r) {
ll mid = (l + r) / 2;
if(check(mid))l = mid + 1;
else r = mid - 1;
}
k = l - 1;
cout<<k<<endl;
check(k);
for(int i = 1; i <= n; ++i){
if(ans[i])cout<<ans[i]<<endl;
else cout<<m<<endl;
}
return 0;
}
位数差
题目描述：
给一个数组{a}，定义 h(a,b)为在十进制下 a + b 与 a 的位数差，求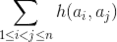 
，0的位数为1。
思路：
分治（递归+二分）
第一反应肯定是暴力，但是一看数据范围直接放弃
接着发现这是区间问题，可以考虑考虑分治，大化小，小化了
[l, r] = [l, mid] + [mid + 1, r]
如何快速的求出h(l, r), 这里肯定不能暴力，我们可以考虑给他排个序，然后就可以去快乐的二分查找，判断比$$10^n$$ - r 大的 l 有多少个，统计下来就是答案：
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll qpow(ll a,ll n){ll ans=1,base=a%mod;while(n){if(n&1)ans=(ans*base)%mod;base=(base*base)%mod;n>>=1;}return ans;}
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll n, l, r, x, y, len, ans;
int tr[MAX];
int br[] = {10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000};
ll cal(ll l, ll r){
if(r == l)return 0;
ll mid = (l + r) / 2;
ll ans = cal(l, mid) + cal(mid + 1, r);
sort(tr + mid + 1, tr + r + 1);
for(ll i = l; i <= mid; ++i){
for(int j = 0; j < 9; ++j){
if(tr[i] < br[j]){
ans += r - (lower_bound(tr + 1 + mid, tr + r + 1, br[j] - tr[i]) - tr) + 1;
}
}
}
return ans;
}
int main(){
n = IntRead();
for(int i = 1; i <= n; ++i)tr[i] = IntRead();
cout<<cal(1, n)<<endl;
return 0;
}
/*
6
1 23
43
77
20
44
*/
Stressful Training
题目描述：
Berland SU holds yet another training contest for its students today. nnn students came, each of them brought his laptop. However, it turned out that everyone has forgot their chargers!
Let students be numbered from 111 to nnn. Laptop of the iii-th student has charge aia_iai at the beginning of the contest and it uses bib_ibi of charge per minute (i.e. if the laptop has ccc charge at the beginning of some minute, it becomes c−bic - b_ic−bi charge at the beginning of the next minute). The whole contest lasts for kkk minutes.
Polycarp (the coach of Berland SU) decided to buy a single charger so that all the students would be able to successfully finish the contest. He buys the charger at the same moment the contest starts.
Polycarp can choose to buy the charger with any non-negative (zero or positive) integer power output. The power output is chosen before the purchase, it can't be changed afterwards. Let the chosen power output be xxx. At the beginning of each minute (from the minute contest starts to the last minute of the contest) he can plug the charger into any of the student's laptops and use it for some integer number of minutes. If the laptop is using bib_ibi charge per minute then it will become bi−xb_i - xbi−x per minute while the charger is plugged in. Negative power usage rate means that the laptop's charge is increasing. The charge of any laptop isn't limited, it can become infinitely large. The charger can be plugged in no more than one laptop at the same time.
The student successfully finishes the contest if the charge of his laptop never is below zero at the beginning of some minute (from the minute contest starts to the last minute of the contest, zero charge is allowed). The charge of the laptop of the minute the contest ends doesn't matter.
Help Polycarp to determine the minimal possible power output the charger should have so that all the students are able to successfully finish the contest. Also report if no such charger exists.
题意：
有n台电脑，一共要撑过k分钟
对于每台电脑，他的初始电量为ai，每分钟消耗电量为bi
问，至少需要一个功率(每分钟)为多大的充电器才能保证[0,k)时间内每一台电脑的电量都不为负
思路：
最大功率的最小值，很显然是二分
但是这个题的check函数极其不好写(╥﹏╥)
首先到底给哪个充电？这就是一个贪心，每次都找能坚持的时间最小的那个，如果坚持的时间相同，我们就选bi大的那个，如果bi也相同，我们就选ai小的那个
所以就需要用结构体来存每个电脑的ai，bi和ci（也就是ai / bi)
同时要用一个优先队列/小根堆来维护
维护的东西就是上面写的那个贪心，这里就要写结构体重载，不然塞不进优先队列
对于每次check(x)时，先选出来ci < k的放进优先队列q中，判断一下对列是否为空，空就返回true，从0循环到k-1（从0开始是因为可能有电脑一次都撑不住，k-1是因为最后一次即比赛结束时电量为多少就已经不在乎了），取出队首，扔出去，判断一下此时他的ci是否小于i，小于的话就说明它撑不到给他充电的时候（就是两个电脑同时缺电，但却只有一个充电器，无法撑住），就return false，然后将加上x的点亮的点重新放进优先队列，循环往复……
再就是会有-1的存在，也就是没有能满足的充电器，此时的check返回的是false，所以我们就在true的地放更新ans，对于没有充电器的情况，就不会运行到r = mid + 1 ， 就不会改ans的值，就只需要初始化ans为-1即可
再就是这个题比较坑的就是，卡输入，不开快读会TLE，再就是输入的数是1e12，所有得开longlong，所以就得用longlong的快读╮(￣▽￣"")╭
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline ll llRead(){ll x(0), t(1);char o (getchar());while (o < '0' || o > '9') {if (o == '-') {t = -1;}o = getchar();}for (; o >= '0' && o <= '9'; o = getchar()) {x = (x << 1) + (x << 3) + (o ^ 48);}return x * t;}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll qpow(ll a,ll n){ll ans=1,base=a%mod;while(n){if(n&1)ans=(ans*base)%mod;base=(base*base)%mod;n>>=1;}return ans;}
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll n, k, ans = -1;
struct ran{
ll a, b, c;
bool operator < (const ran &X)const{
if(X.c != c)return c > X.c;
else if(X.b != b)return b < X.b;
return a > X.a;
}
}tr[MAX], now, nextt;
bool check(ll x){
priority_queue<ran>q;
for(int i = 1; i <= n; ++i){
if(tr[i].c < k)q.push(tr[i]);
}
if(q.empty())return true;
for(int i = 0; i < k; ++i){
now = q.top();q.pop();
if(now.c < i)return false;
if((now.a + x) / now.b < k){
nextt.a = now.a + x;
nextt.b = now.b;
nextt.c = nextt.a / nextt.b;
q.push(nextt);
}
if(q.empty())return true;
}
return true;
}
int main(){
n = llRead();k = llRead();
for(int i = 1; i <= n; ++i)tr[i].a = llRead();
for(int i = 1; i <= n; ++i){
tr[i].b = llRead();
tr[i].c = tr[i].a / tr[i].b;
}
ll l = 0, r = 2e12;
while (l <= r){
ll mid = (l + r) / 2;
if(check(mid)){
ans = mid;
r = mid - 1;
}
else l = mid + 1;
}
cout<<ans<<endl;
return 0;
}
华华给月月准备礼物
题目描述：
二月中旬虐狗节前夕，华华决定给月月准备一份礼物。为了搭建礼物的底座，华华需要若干根同样长的木棍。华华手头上有一些长度参差不齐的木棍，他想将每根都裁剪成若干段自己想要的长度，并丢掉多余的部分。因为华华的手很巧，所以他的裁剪过程不会有任何的失误。也就是说，对于一根长度为N的木棍，华华可以精准的将它们裁剪为若干段木棍，使它们的长度之和为N。
华华不知道裁剪成多长比较好，所以干脆越长越好。不过由于华华有点强迫症，所以他希望长度为非负整数。保证所有木棍的原长也是非负整数。那么请问华华最终得到的每根木棍多长呢？
思路：
真就一眼题，直接莽二分
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using namespace std;
#define inf 0x3f3f3f3f
#define MAX 1000000 + 50
#define endl '\n'
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef long long ll ;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline ll llRead(){ll x(0), t(1);char o (getchar());while (o < '0' || o > '9') {if (o == '-') {t = -1;}o = getchar();}for (; o >= '0' && o <= '9'; o = getchar()) {x = (x << 1) + (x << 3) + (o ^ 48);}return x * t;}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll qpow(ll a,ll n){ll ans=1,base=a%mod;while(n){if(n&1)ans=(ans*base)%mod;base=(base*base)%mod;n>>=1;}return ans;}
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll n, k;
ll tr[MAX];
bool check(ll x){
ll sum = 0;
for(int i = 1; i <= n; ++i){
sum += (tr[i] / x);
}
if(sum >= k)return true;
else return false;
}
int main(){
cin>>n>>k;
for(int i = 1; i <=n; ++i)cin>>tr[i];
ll l = 1, r = 2*inf;
while (l <= r) {
ll mid = (l + r) / 2;
if(check(mid))l = mid + 1;
else r = mid - 1;
}
cout<<l - 1<<endl;
return 0;
}
