矩形覆盖问题：变相斐波纳契数列

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

观察题目中的矩形，2*n的，是个长条形。本来脑中想象的是复杂的华容道，但是既然只是简单的长条形，那么依然逆向分析。既然是长条形的，那么从后向前，最后一个矩形2*2的，只有两种情况：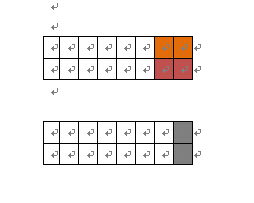　　 

1、第一种是最后是由一个2*(n-1)的矩形加上一个竖着的2*1的矩形　　

2、另一种是由一个2*(n-2)的矩形，加上两个横着的2*1的矩形，因此我们可以得出，第2*n个矩形的覆盖方法等于第2*(n-1)加上第2*(n-2)的方法。

```python
f = lambda n: 1 if n < 2 else f(n - 1) + f(n - 2)
```