压缩维度oj P1173+P1174+P1164
今天在洛谷上刷dp,忽然冒出一道求最大字段和的问题,然后忘了瞬间忘了这是dp,几分钟一个贪心出来了成功ac,忽然想起自己在作dp,于是乖乖刷dp。
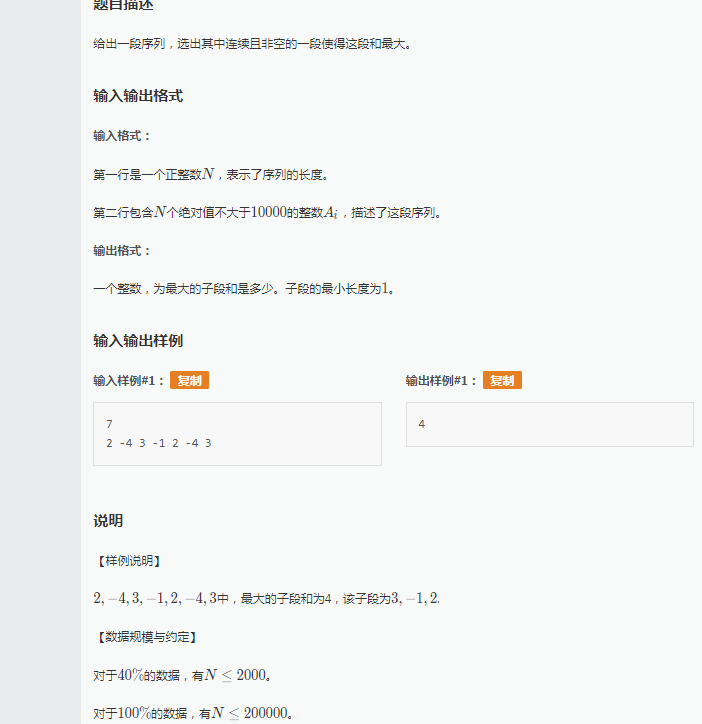
这个可能很多人都会但是今天有4种解法哦,本人只尝试了3种解法。
NO.1:明显一个贪心一个sum求当前的累加和如果小于0就清零,继续累加并不断去max即可。

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline long long read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n; int a[200009]; int ans=0; int maxx=-1111111; int main() { //freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++)a[i]=read(); for(int i=1;i<=n;i++) { ans+=a[i]; if(ans>maxx) { maxx=ans; } if(ans<0) ans=0; } printf("%d\n",maxx); return 0; }
NO.2:说是要练dp嘛,然后点开题解看dalao们的dp,f[i]=max(f[i-1],a[i]);这样最大值在f[i]之中,最后找max即可。

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline long long read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n; int a[200009]; int f[200009]; int ans=-1111111; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); f[i]=max(f[i-1]+a[i],a[i]); ans=max(f[i],ans); } cout<<ans<<endl; return 0; }
NO.3:题解之中有一个分治的想法,十分巧妙的把所有情况递归出来从而求解。在每一个区间之中取max即可。

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline long long read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=-1111111; int n; int a[200009]; int bwy(int x,int y) { if(x==y)return a[x]; int mid=(x+y)>>1; int maxx=maxn,maxx1=maxn,sum=0; for(int i=mid;i>=x;i--){sum+=a[i];maxx=max(maxx,sum);}sum=0; for(int i=mid+1;i<=y;i++){sum+=a[i];maxx1=max(maxx1,sum);} return max(max(bwy(x,mid),bwy(mid+1,y)),maxx+maxx1); } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++)a[i]=read(); printf("%d\n",bwy(1,n)); return 0; }
这个就比较难理解了,要多看看。
No.4:有大神用的是线段树来维护,tql,我不想打线段树代码就没有了。。。
下面回到了本校oj看起来以前过得题想要再想想。求最大连续子矩阵累加和,这个就要压缩维度了。
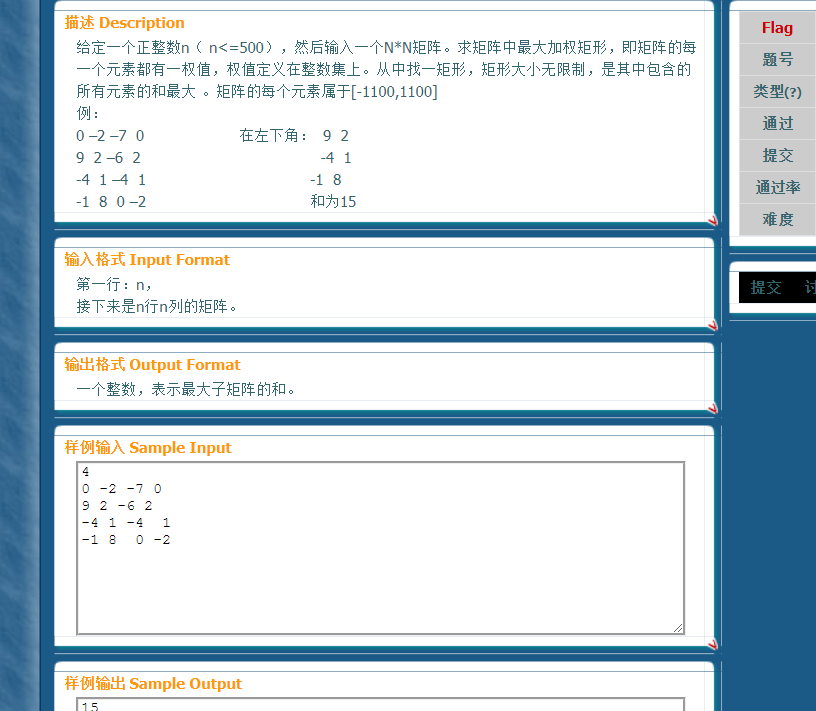
仔细想想,我可以先把每一列的前缀和全部求出来进行维度的压缩,然用一个一维数组来表示第几列从第i行到第j行的累加,十分巧妙的思想,我想了十几分钟才搞懂。这样的话就可以便利到每一个矩阵了,十分巧妙!!!

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline long long read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=505; int n,a[maxn][maxn],tmp[maxn],maxx=-1100000,ans=0; int main() { freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { maxx=read(); a[i][j]=a[i-1][j]+maxx;//前缀和 } maxx=-1100000; for(int i=1;i<=n;i++) { for(int j=i;j<=n;j++) { ans=0;//注意便利下一个矩阵的时候ans要清零。 for(int k=1;k<=n;k++) { tmp[k]=a[j][k]-a[i-1][k]; ans+=tmp[k]; if(ans>maxx)maxx=ans; if(ans<0)ans=0; } } } printf("%d\n",maxx); return 0; }
然后还有很难的三维压缩qwq真不想写。。。
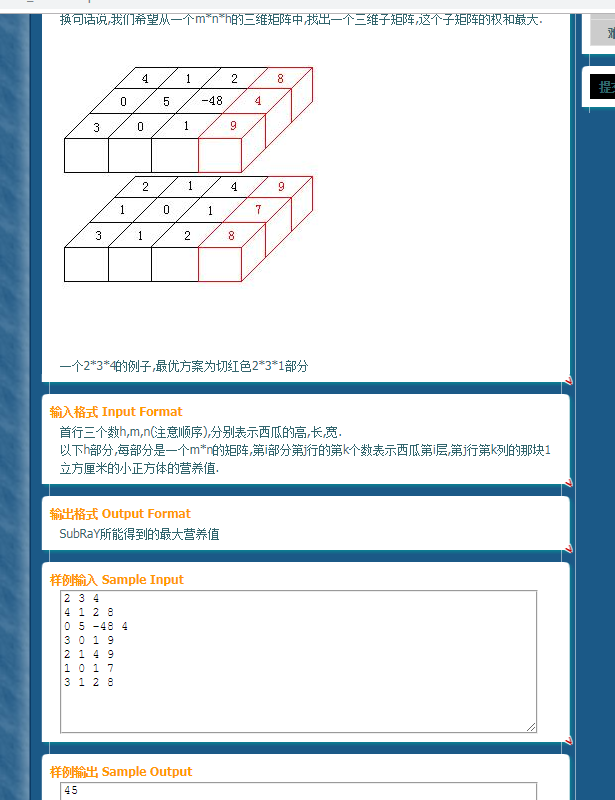
三维的压缩,但首先要看懂题。
看着学长的代码自慢慢干,发现书上的方法并不是很优,还不如和第二题一样进行压缩。
a[i][j][k]+=a[i-1][j][k];压缩高度——c[k][u]=a[j][k][u]-a[i-1][k][u];再取任意宽度和长度的立方体块压到一个二维数组之中实现任意立方体小块的拿取,
这样就可以了,c[k][u]+=c[k][u-1];压缩宽度这样就和上一题一样开始压缩二维数组,取任意矩阵的和。b[x]=c[x][u]-c[x][k-1];——这样压缩到一维的数组里面取任意的矩阵然后用求最大字段和就行了。是很难理解的表示不想手动模拟一遍。。。
代码:

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline long long read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int a[101][101][101],c[101][101],b[101],ans,maxx=-1000000; int n,h,m; int main() { //freopen("1.in","r",stdin); h=read();m=read();n=read(); for(int i=1;i<=h;i++)for(int j=1;j<=m;j++)for(int k=1;k<=n;k++) a[i][j][k]=read(),a[i][j][k]+=a[i-1][j][k]; for(int i=1;i<=h;i++)for(int j=i;j<=h;j++) { for(int k=1;k<=m;k++)for(int u=1;u<=n;u++) { c[k][u]=a[j][k][u]-a[i-1][k][u]; c[k][u]+=c[k][u-1]; } for(int k=1;k<=n;k++)for(int u=k;u<=n;u++) { ans=0; for(int x=1;x<=m;x++) { b[x]=c[x][u]-c[x][k-1]; ans+=b[x]; if(ans>maxx)maxx=ans; if(ans<0)ans=0; } } } printf("%d\n",maxx); return 0; }
大功告成啦。。。
如果你的青春感到迷茫,那就对了,因为谁的青春不迷茫。
b[x]=c[x][u]-c[x][k-1];



 浙公网安备 33010602011771号
浙公网安备 33010602011771号