7.30 NOI模拟赛 B Easy Sum 分块 NTT
LINK:Easy Sum

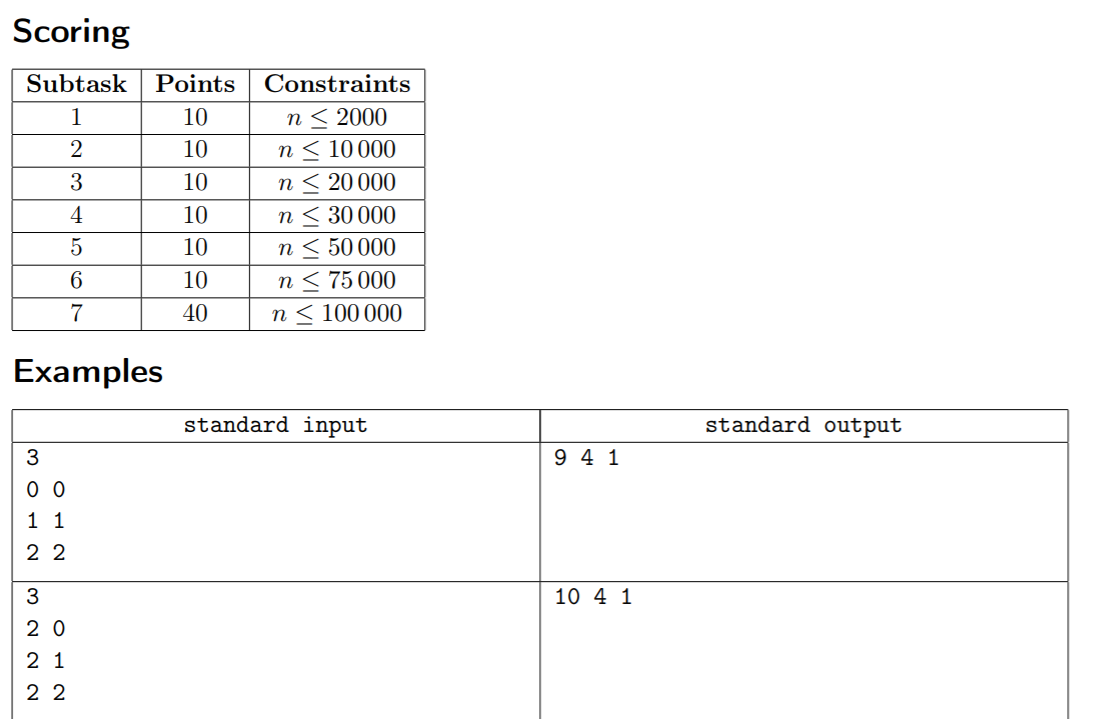
考试的时候一脸懵逼 想不通这个\(n^2\)的还能怎么优化.
事实上暴力\(n^2\)有30~40 而我脸黑 只有30 很气...
把点抽象到杨辉三角上可以发现这是若干个行上的K个点求和 如果是对列上求和或者总体求和就好做的多.
另外一种\(n^2\)是 这n个点从\((a_i,b_i)\)这个位置走到\((0,k)\)
实际上在图上进行dp求方案 很多神仙使用滚动数组+循环展开\(n^2\)暴力过了这道题.
正解是这样的:
将坐标分块 这样做是方便后续的转移.
考虑隔B分上一块然后我们维护每一列的的dp值 从上一块dp到下一块.
每次由上一列dp到下一列需要做一个前缀和的东西(实际上是后缀和.
其实就是乘以多项式\(\frac{1}{(1-x)}\)跳B列就乘以\(\frac{1}{(1-x)^B}\)
可能会有疑问为什么不直接跳第一列而是一块一块跳.
在跳的过程中存在一个点要对下一列有贡献了 所以我们此时暴力加上贡献还是\(n^2\)的.
不妨考虑加到上一次要跳的那一列 这样计算出自己需要res次前缀和 那么就是给上次的列的多项式加上一个\(x^y\cdot (1-x)^{B-res}\)
这个多项式最长只有B所以就可以接受了.
总复杂度为\(n\cdot B+\frac{n}{B}\cdot nlogn\) 显然当B取\(\sqrt{nlogn}\)时最优.
代码写的很容易理解.
这个思路是真的妙 建议一写.
code
//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<queue>
#include<deque>
#include<stack>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define inf 1000000000000000ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x];i;i=nex[i])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 13331ll
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-5
#define sq sqrt
#define S second
#define F first
#define mod 998244353
#define md 1000000007
#define max(x,y) ((x)<(y)?y:x)
#define a(i) t[i].a
#define b(i) t[i].b
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
RE int x=0,f=1;RE char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
inline ll Read()
{
RE ll x=0,f=1;RE char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
const int MAXN=350010,maxn=100010,N=2000,G=3;
int lim=1,n,B,m,INV,IG;
int fac[MAXN],inv[MAXN],h[N][N];
int f[MAXN],g[MAXN],rev[MAXN],O[MAXN];
struct wy{int a,b;}t[maxn];
vector<int>w[N];
inline int ksm(int b,int p)
{
int cnt=1;
while(p)
{
if(p&1)cnt=(ll)cnt*b%mod;
b=(ll)b*b%mod;p=p>>1;
}
return cnt;
}
inline int C(int a,int b){return (ll)fac[a]*inv[b]%mod*inv[a-b]%mod;}
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline void NTT(int *a,int op)
{
vep(0,lim,i)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=2;len<=lim;len=len<<1)
{
int mid=len>>1;
int wn=ksm(op==1?G:IG,(mod-1)/len);
vep(1,mid,j)O[j]=(ll)O[j-1]*wn%mod;
for(int j=0;j<lim;j+=len)
{
vep(0,mid,i)
{
int x=(ll)a[i+j+mid]*O[i]%mod;
a[i+j+mid]=(a[i+j]-x+mod)%mod;
a[i+j]=add(a[i+j],x);
}
}
}
if(op==-1)vep(0,lim,i)a[i]=(ll)a[i]*INV%mod;
}
inline bool cmp(wy x,wy y){return x.a<y.a;}
int main()
{
//freopen("1.in","r",stdin);
n=read();B=(int)sqrt(n*20*1.0);
rep(1,n,i)get(a(i)),get(b(i));
lim=1;while(lim<=2*n)lim=lim<<1;
vep(0,lim,i)rev[i]=rev[i>>1]>>1|((i&1)?lim>>1:0);
m=n+B;INV=ksm(lim,mod-2);IG=ksm(G,mod-2);O[0]=1;
fac[0]=1;rep(1,m,i)fac[i]=(ll)fac[i-1]*i%mod;
inv[m]=ksm(fac[m],mod-2);fep(m-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
rep(0,n,i)g[i]=C(i+B-1,B-1);
NTT(g,1);//NTT(g,-1);
rep(0,B,i)
rep(0,i,j)
h[i][j]=(ll)C(i,j)*((j&1)?mod-1:1)%mod;
sort(t+1,t+1+n,cmp);int BB=n/B+1;
rep(1,n,i)w[a(i)/B+1].pb(i);
fep(BB,1,k)
{
vep(0,(int)w[k].size(),j)
{
int id=w[k][j];
int y=n-b(id);
int res=a(id)%B+1;
//(1-x)^{B-res}*x^y
rep(0,B-res,i)if(y+i<=n)f[y+i]=add(f[y+i],h[B-res][i]);
}
NTT(f,1);
vep(0,lim,i)f[i]=(ll)f[i]*g[i]%mod;
NTT(f,-1);
vep(n+1,lim,i)f[i]=0;
}
rep(0,n-1,i)printf("%d ",f[n-i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号