6.15 省选模拟赛 复活石 狄利克雷卷积 快速幂 数论

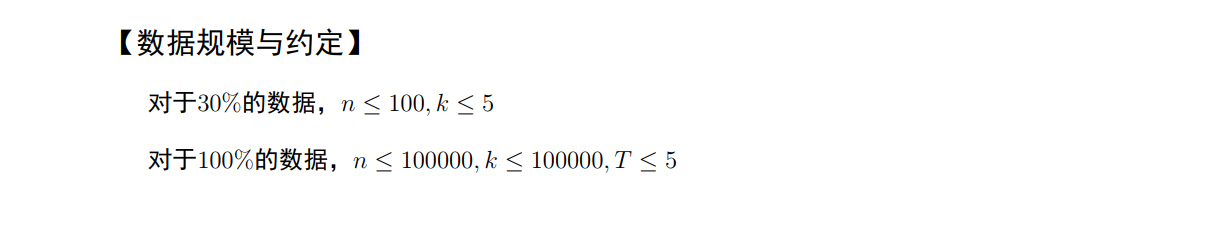
这种题目 不算是很套路的数论。

暴力的想法是逐位做 复杂度为\(k\cdot n\cdot ln^n\)

容易联想到狄利克雷卷积 只要给最后一个卷积一个I函数即可。

由于狄利克雷卷积 具有交换律和结合律 所以原式=\(I^k*f\)

前者显然可以快速幂做 所以复杂度为\(n\cdot ln^n\cdot logk\)

值得注意的是 模数问题 今天过于sb 没检查 导致模数写错了。

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 100000000000000000ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x)
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-8
#define sq sqrt
#define S second
#define F first
#define mod 1000000007
#define y(x) t[x].y
#define x(w) t[w].x
#define min(x,y) ((x)>(y)?(y):(x))
#define Set(a,v) memset(a,v,sizeof(a))
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
//fate stay night
const int MAXN=100010;
int n,T,k;
int f[MAXN],g[MAXN],h[MAXN],I[MAXN];//h*f
int A[MAXN],B[MAXN];
inline void add(int &x,int y){x=x+y>=mod?x+y-mod:x+y;}
inline void NTT(int *a,int *b)
{
	rep(1,n,i)A[i]=a[i],B[i]=b[i],a[i]=0;
	rep(1,n,i)for(int j=i,w=1;j<=n;j+=i,++w)add(a[j],(ll)A[i]*B[w]%mod);
}
int main()
{
	freopen("b.in","r",stdin);
	freopen("b.out","w",stdout);
	get(T);
	while(T--)
	{
		get(n);get(k);
		rep(1,n,i)get(f[i]);
		rep(1,n,i)I[i]=1;h[1]=1;
		while(k)
		{
			if(k&1)NTT(h,I);
			NTT(I,I);k=k>>1;
		}
		NTT(h,f);
		rep(1,n,i)put_(h[i]),h[i]=f[i]=I[i]=0;
		puts("");
	}
	return 0;
}