6.15 省选模拟赛 老魔杖 博弈论 SG函数

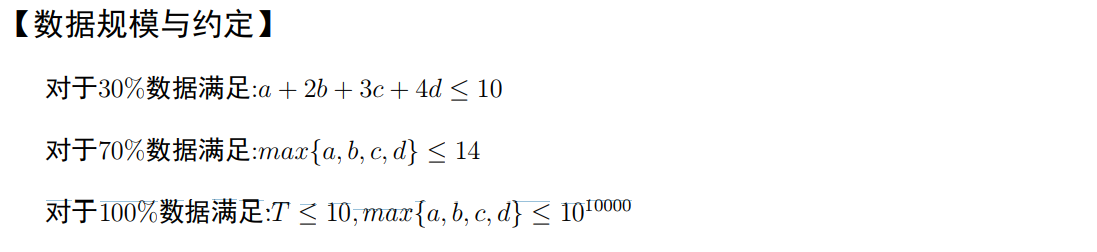
这道题确实没有一个很好的解决办法 唯一的正解可能就是打表找规律 或者 直接猜结论了吧。

尽管如此 在此也给最终结论一个完整的证明。

对于70分 容易发现状态数量不大 可以进行暴力dp求SG函数。

原本打算打表 实测状态数量只有1e5左右。

const int maxn=800;
int T,ans;
int vis[100010];
int f[141][58][30][15];//表示当前状态为这个东西时的SG函数.
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	int lim1=140,lim2=56,lim3=28,lim4=14;
	rep(0,lim4,w)rep(0,lim3,k)
	rep(0,lim2,j)rep(0,lim1,i)
	{
		if(4*w+3*k+2*j+i>140)continue;
		if(i>=1)vis[f[i-1][j][k][w]]=1;
		if(j>=2)vis[f[i][j-2][k][w]]=1;
		if(k>=3)vis[f[i][j][k-3][w]]=1;
		if(w>=4)vis[f[i][j][k][w-4]]=1;
		if(j>=1)vis[f[i+2][j-1][k][w]]=1;
		if(k>=1)vis[f[i+1][j+1][k-1][w]]=1;
		if(w>=1)vis[f[i+1][j][k+1][w-1]]=1,vis[f[i][j+2][k][w-1]]=1;
		int cnt=0;
		while(vis[cnt])++cnt;
		f[i][j][k][w]=cnt;
		if(i>=1)vis[f[i-1][j][k][w]]=0;
		if(j>=2)vis[f[i][j-2][k][w]]=0;
		if(k>=3)vis[f[i][j][k-3][w]]=0;
		if(w>=4)vis[f[i][j][k][w-4]]=0;
		if(j>=1)vis[f[i+2][j-1][k][w]]=0;
		if(k>=1)vis[f[i+1][j+1][k-1][w]]=0;
		if(w>=1)vis[f[i+1][j][k+1][w-1]]=0,vis[f[i][j+2][k][w-1]]=0;
		++ans;
	}
	get(T);
	while(T--)
	{
		int get(a),get(b),get(c),get(d);
		put(f[a][b][c][d]?1:0);
	}
	return 0;
}

先放张图 ，设 l=(a+c)%2,r=(b+d)%3;如果l!=r 先手必胜反之后手必胜。

证明：l==r时采取上面的8种操作 都会转到一个必胜局面l!=r.

考虑 l!=r的必胜局面 可以发现此时先手一定还可以操作。

且此时一定可以转到l==r的局面。

考虑\(r-l=-1,1,2\).

当\(r-l==-1\) 时 此时(1)(6)操作可以使得 \(l==r\) 且 (1)(6)其中必有一个满足。

当\(r-l==1\) 时 此时(5)(7)操作可以使得 \(l==r\) 且 (5)(7)其中必有一个满足。

当\(r-l==2\) 时 此时(2)(8)操作可以使得 \(l==r\) 且 (2)(8)其中必有一个满足。

至此 所有必胜的局面都可以转移到必败的局面 必败的局面一定可以转移到必胜的局面。

所以必胜和必败局面成立。

char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline int read2()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=(x*10+ch-'0')%2;ch=getc();}
    return x*f;
}
inline int read3()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=(x*10+ch-'0')%3;ch=getc();}
    return x*f;
}
const int maxn=800;
int T,ans;
int vis[100010];
int f[141][58][30][15];
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	get(T);
	while(T--)
	{
		int a=read2();
		int b=read3();
		a=(a+read2())%2;
		b=(b+read3())%3;
		put(a!=b?1:0);
	}
	return 0;
}