5.12 省选模拟赛 T2 贪心 dp 搜索 差分
LINK:T2
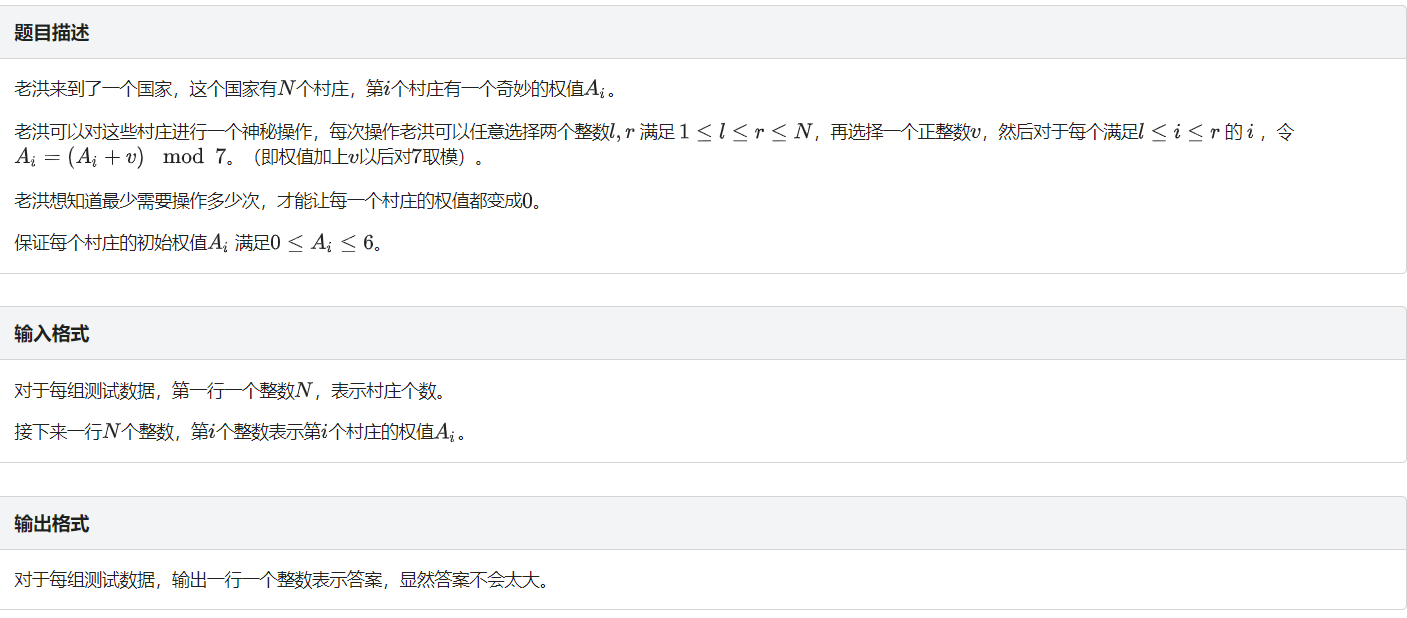

这题感觉很套路 但是不会写.
区间操作 显然直接使用dp不太行 直接爆搜也不太行复杂度太高.
容易想到差分 由于使得整个序列都为0 那么第一个数也要i差分前一个数 强行加一个0 然后 显然让差分序列变成0即可。
每次可以单点修改两个位置的值 也可以当前和最后一个数后面那个数做 其实相当于单独做 表示后缀全体的事情。
0显然没有任何贡献了 考虑怎么做才是最优的。
当时没有证明 直接猜了一个结论是 每次操作比然会使一个位置上的值变成0.
(当时以为假了 结果时当时没有想清楚 自闭...
证明 如果存在一次操作使得两个数字没有一个变成0 那么在接下来的最优操作中 这个两个数字必然还会被选择 如果此时存在最优策略两次让4个数字变成0.
那么换成原来的 此时已经 拥有三次机会 让其中三个变成0 之后那第四个数字也会变成0 因为可以认为这四个数字时一组 最优需要三次。
那么 他们的总和确定 需要的值确定 其他三个变成后 剩下的值会让第四个值变成0.
至此可以发现前者策略造成的结果不差于后者.
还有一个小结论:
能一次消掉两个数字就直接消掉 因为从结果上看是当前最优.
对后续局面来看当前决策相对于其他决策也不会更差.
每次消的时候 可以发现 一个数字加上一个值 一个数字减掉一个值 这样做在%7意义下 之和为7.
那么1,6 2,5, 3,4 肯定是这些数字配对。
配对过后可以发现最多只剩下三种数字。
这个时候我选择了爆搜 因为 可能一些分组策略使得结果更优.
值得一提的是 这里爆搜复杂度海星 其实还可以更快就是爆搜多带一个属性为当前的值 正确性可以保证.
在数据随机的情况下确实可以得到60分 当时我以为写了个假代码(原来很稳..
const int MAXN=510;
int n,cnt,ans,num;
int a[MAXN],vis[MAXN],b[MAXN],w[MAXN],c[MAXN];
inline void dfs(int x,int v)
{
if(v>=ans)return;
if(x==num+1){ans=v;return;}
int mx;
rep(1,mod-1,i)if(b[i]){mx=i;break;}
--b[mx];dfs(x+1,v+1);
int ww=mod-mx;
if(b[ww])
{
--b[ww];
dfs(x+2,v+1);
++b[ww];
}
rep(1,mod-1,i)
{
if(b[i]&&i!=ww)
{
int cc=(i-ww+mod)%mod;
++b[cc];--b[i];
if(!cc)dfs(x+2,v+1);
else dfs(x+1,v+1);
--b[cc];++b[i];
}
}
++b[mx];
}
int main()
{
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
get(n);rep(1,n,i)get(w[i]);
rep(2,n,i)a[i]=w[i]-w[i-1];a[1]=w[1];
rep(1,n,i)rep(1,n,j)
{
if(!a[j]||!a[i])continue;
if(vis[i]||vis[j])continue;
if(a[i]==-a[j]||mod-a[i]==a[j]){vis[i]=vis[j]=1;++cnt;break;}
}
rep(1,n,i)if(!vis[i]&&a[i])++b[(a[i]+mod)%mod],++num;
ans=num;dfs(1,0);put(ans+cnt);return 0;
}
考虑优化.
容易想到这个爆搜的过程可以记忆化搜索 且 状态量不到1e8 可以直接搜。
可以直接dp f[i][j][k][w]表示前三种数字的数量以及当前积攒的值为w的最小操作次数.
这是后续了 我后来用了题解的状态 表示积攒的值为w的最大分组.
因为 我原本的想法时让每一个数字变成0 然后和其他数字配对可以产生一些效果.
而这里时让一些数字分组 每个组内最后一个数字是不需要被操作的。
两个状态等效 不过后者秒一点 每个组内和显然为7的倍数. 而前者也是如此.
值得注意的是 最后可能有一组不能恰好变成0 那么可以借用最后一个数字的后面的数字来做。
不过这组是不产生效果的。需要滚动数组来优化.
const int MAXN=510;
int n,cnt,ans,num;
int v1,v2,v3,c1,c2,c3;
int a[MAXN],w[MAXN],c[MAXN];
int f[2][MAXN][MAXN][7];//前i个x j个y k个z 当前大小为c所分的最多的组数.
inline int M(int x){return (x%mod+mod)%mod;}
inline void dp()
{
int u=0;
memset(f,-1,sizeof(f));
f[0][0][0][0]=0;
rep(0,c1,i)
{
u=u^1;
rep(0,c2,j)rep(0,c3,k)rep(0,mod-1,s)f[u][j][k][s]=-1;
rep(0,c2,j)
rep(0,c3,k)
{
rep(0,mod-1,s)
{
if(f[u^1][j][k][s]==-1)continue;
if(i+1<=c1)
{
int ww=M(v1+s);
f[u][j][k][ww]=max(f[u][j][k][ww],f[u^1][j][k][s]+(s==0));
}
if(j+1<=c2)
{
int ww=M(v2+s);
f[u^1][j+1][k][ww]=max(f[u^1][j+1][k][ww],f[u^1][j][k][s]+(s==0));
}
if(k+1<=c3)
{
int ww=M(v3+s);
f[u^1][j][k+1][ww]=max(f[u^1][j][k+1][ww],f[u^1][j][k][s]+(s==0));
}
}
}
}
rep(0,mod-1,s)ans=max(ans,f[u^1][c2][c3][s]-(s!=0));
}
int main()
{
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
get(n);rep(1,n,i)get(w[i]);
rep(2,n,i)a[i]=w[i]-w[i-1];a[1]=w[1];
rep(1,n,i)a[i]=M(a[i]),++c[a[i]];
int w1=min(c[1],c[6]);cnt+=w1;
if(c[1]>c[6])c1=c[1]-w1,v1=1;else c1=c[6]-w1,v1=6;
w1=min(c[2],c[5]);cnt+=w1;
if(c[2]>c[5])c2=c[2]-w1,v2=2;else c2=c[5]-w1,v2=5;
w1=min(c[3],c[4]);cnt+=w1;
if(c[3]>c[4])c3=c[3]-w1,v3=3;else c3=c[4]-w1,v3=4;
dp();cnt=cnt+c1+c2+c3-ans;put(cnt);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号