4.24 省选模拟赛 一丝补给 贪心 可并堆

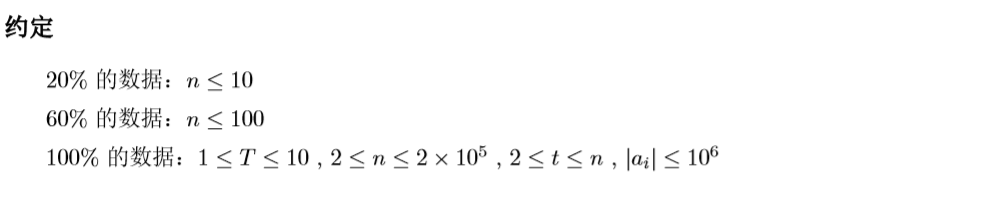
神题 上午想了很久 都没有得到一个比较优秀的做法。

对于n<=10 可以状压可以爆搜 复杂度差不多。

接下来就需要考虑正解了。

容易发现 很难非dp 因为状态的无序性很强 也比较类似贪心。

那么我们贪心的策略就很明显了：优先吃掉代价小的且是正收益的东西不断壮大自身最终到达目标点。

如何判断这一点,因为一些正权值的点可能可以被负权值的点给笼罩住。

考虑一个点选和不选的情况。

可以得到一个比较易得的结论 一个叶子节点权值为负 此时如果不是终止节点 那么选择一定不优。

进一步 我们可以将这个结论拓展到一个点所在的连通块 如果价值为负那么一定不选。

那么初始情况 所有点都是独自的连通块 连通块之间可以合并 因为存在树上拓扑序 一个点选择与否和其他点有关 如果仅凭当前点所在联通块的价值选还是不选那么会对后面的点造成影响。

进一步的 可以考虑把所有有用的连通块给处理出来。

如 对于一个点x 如果其权值为负 那么如果其不和叶子节点合并 那么x这个点是不会被选择的。

同时 还可以发现合并的时候 尽量选择 代价较小的合并 因为对于后面求答案的时候 如果当前是不需要合并的 可能会因为合并带来的结果更差。

换个说法 合并代价较小的连通块一定不会比合并代价大的联通块结果更差。

值得一提的是 此时显然是父亲合并儿子 递归的想 儿子此时 连通块的权值必然为正。不然合并也是无意义的。

于是就得到了一个做法。

对于某个点权值为负 这个点有价值当且仅当和儿子进行合并。

处理 几种情况。设 当前代价,获得 分别为 px,gx.设儿子代价,获得 分别为 pv,gv.

存在 gx>px,px<pv,gv>pv 时 可以不合并 相对于合并 结果不会更差更优。(因为一旦合并这就意味着要访问这个连通块需要衡量整体的代价 合并必然使代价不降。

但是 代价为负的时候必要合并。

gx>px,px>pv,gv>pv 时 此时可以发现 我们如果能够到x 那么必然能够到v 所以此时合并不合并是一样的。

剩下两种情况就是 代价为负了 必然合并 且 先合并较小的 结果不会更差。

综上 把整颗树变成了若干个连通块了。

然后我们只需要一直把这些代价为正的连通块从小到大便利到 看一下最后能否便利到目标点即可。

这里有一个小trick 将目标点下方挂一个点 权值为正无穷 也就是说这个点必然出现在联通块中 所以一路从代价从小到大走下去即可。

至此 把所有 最优情况列举出来了 所以按照原来的贪心策略即可。

const int MAXN=200010;
int n,T,len,flag,mark,id;
ll a[MAXN];int l[MAXN],r[MAXN],rt[MAXN],h[MAXN];
int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1];
pii w[MAXN];
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
inline bool operator <(const pii a,const pii b)
{
	return a.F==b.F?a.S>b.S:a.F<b.F;
}
inline int merge(int x,int y)
{
	if(!x||!y)return x|y;
	if(w[x]>w[y])swap(x,y);
	r[x]=merge(r[x],y);
	if(h[l[x]]<h[r[x]])swap(l[x],r[x]);
	h[x]=h[r[x]]+1;return x;
}
inline int get_new(ll x,ll y)
{
	++id;h[id]=l[id]=r[id]=0;
	w[id].F=x;w[id].S=y;
	return id;
}
inline void dfs(int x,int fa)
{
	go(x)
	{
		if(tn==fa)continue;
		dfs(tn,x);
		rt[x]=merge(rt[x],rt[tn]);
	}
	ll p,g;
	if(a[x]>0)p=0,g=a[x];
	else p=-a[x],g=0;
	while(rt[x])
	{
		ll pp=w[rt[x]].F,gg=w[rt[x]].S;
		if(g>p&&p<pp)break;
		if(g>pp)g+=gg-pp;
		else p+=pp-g,g=gg;
		rt[x]=merge(l[rt[x]],r[rt[x]]);
	}
	if(g>p)rt[x]=merge(rt[x],get_new(p,g));
}
int main()
{
	freopen("escape.in","r",stdin);
	freopen("escape.out","w",stdout);
	get(T);
	while(T--)
	{
		rep(1,n+1,i)lin[i]=0,rt[i]=0;id=0;
		len=0;get(n);get(mark);
		rep(1,n,i)get(a[i]);
		rep(2,n,i)
		{
			int x,y;
			get(x);get(y);
			add(x,y);add(y,x);
		}
		++n;add(mark,n);add(n,mark);
		a[n]=INF;dfs(1,0);
		ll ww=0;
		while(rt[1])
		{
			if(ww>=w[rt[1]].F)
			{
				ww+=w[rt[1]].S-w[rt[1]].F;
				rt[1]=merge(l[rt[1]],r[rt[1]]);
			}
			else break;
		}
		if(ww>=INF)puts("escaped");
		else puts("trapped");
	}
	return 0;
}