4.22 省选模拟赛 最优价值 网络流 最大权闭合子图

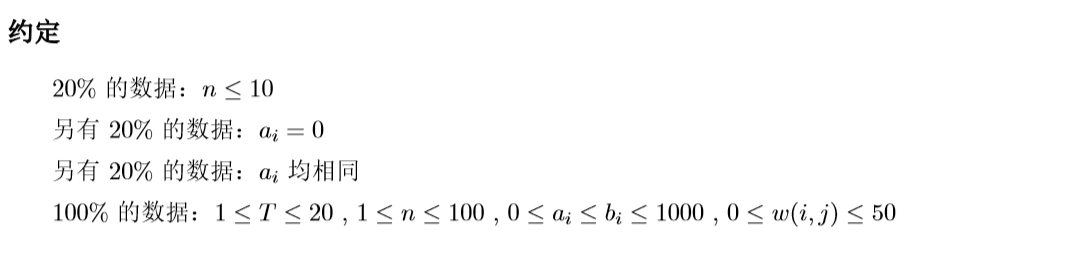
这道题涉及了一个很久以前会的知识点 考试的时候建图硬是没想出来 真自闭。
对于n<=10 容易发现可以爆搜全排列 期望的得分20.
对于\(a_i=0\) 观察发现方阵中的值都为正数 这意味着某种数字选多少都行 有关的是当前这种数字选了没有。
数字只有10个 爆搜某种数字选了没有即可。
40 code: 不过值得一提的是多组数据 考试的时候ans没清0 导致爆零。
const int MAXN=110;
int T,n,ans;
char a[MAXN];int b[MAXN][MAXN];
struct wy{int a,b;}w[MAXN];
int vis[MAXN],mark[MAXN];
inline void dfs(int x)
{
if(x==n+1)
{
int cnt=0;
rep(1,n,i)if(vis[i])++mark[a[i]-'0'];
rep(0,9,i)if(mark[i])cnt=cnt-((mark[i]-1)*w[i].a+w[i].b);
rep(1,n,i)
{
if(!vis[i])continue;
rep(1,n,j)if(vis[j])cnt+=b[i][j];
}
ans=max(ans,cnt);
rep(0,9,i)mark[i]=0;
return;
}
vis[x]=1;
dfs(x+1);
vis[x]=0;
dfs(x+1);
}
inline void dfs1(int x)
{
if(x==10)
{
int cnt=0;
rep(0,9,i)if(vis[i])cnt-=w[i].b;
rep(1,n,i)
{
if(!vis[a[i]-'0'])continue;
rep(1,n,j)
{
if(!vis[a[j]-'0'])continue;
cnt+=b[i][j];
}
}
ans=max(ans,cnt);
return;
}
vis[x]=1;
dfs1(x+1);
vis[x]=0;
dfs1(x+1);
}
int main()
{
freopen("value.in","r",stdin);
freopen("value.out","w",stdout);
gt(T);
while(T--)
{
gt(n);gc(a);ans=0;
int flag1=0;
rep(0,9,i)
{
int x,y;gt(x);gt(y);
if(x!=flag1)flag1=1;
w[i]=(wy){x,y};
}
rep(1,n,i)rep(1,n,j)
{
gt(b[i][j]);
if(i==j)b[i][j]=0;
}
if(n<=10)
{
dfs(1);
put(ans);
continue;
}
if(!flag1)
{
dfs1(0);
put(ans);
continue;
}
}
return 0;
}
考虑正解。
容易发现 这道题是不能dp的 同时由于n<=100.且求最大值提示算法网络流。
考虑建图 如果把行列建点 那么一些代价很难被体现出来也毫无道理可言。
考虑模拟费用流 可以发现 在一定程度上一个点的退出加入是不满足费用的单调性的 所以费用流无法解决。
考虑最大权闭合子图。容易发现一个点选择了 必然会选择这个点所在的位置 这个点所在位置选择了必然会选择之后的字符位置。
可以发现这是一张闭合无向图。我们尝试把点权加上 对于一类点显然是其原本的价值。对于二类点显然为-a.对于三类点 显然为-b+a.
这样就构成了最大权闭合子图的基本模型。只要从中选出一张子图使其点权和最大即可 同时可以发现满足题目要求。
值得注意的是:
连边的时候要判断权值为正还是为负 为正加起来 跑最小割。
最后总权值-最小割即可。含义:割掉的显然是最小的边权和 要么是不选的 要么是选的 需要花费代价的。
合法性:可以看出这样建图 某个点一旦选择了就付出了相应的代价 所以是合法的。
最优性:正权值和为定值-(要选择的代价+不选择的付出) 由于后者为最小割 所以保证了最小。
const int MAXN=110,maxn=MAXN*MAXN+MAXN;
int TT,n,S,T,cnt,ans,len;
char a[MAXN];
int b[MAXN][MAXN],q[maxn],vis[maxn],cur[maxn];
int s1[MAXN],s2[MAXN],w[MAXN],c[MAXN];
int lin[maxn],nex[MAXN*MAXN<<4],ver[MAXN*MAXN<<4],e[MAXN*MAXN<<4];
inline void add(int x,int y,int z)
{
ver[++len]=y;nex[len]=lin[x];lin[x]=len;e[len]=z;
ver[++len]=x;nex[len]=lin[y];lin[y]=len;e[len]=0;
}
inline int bfs()
{
rep(1,cnt,i)cur[i]=lin[i],vis[i]=0;
int l=0,r=0;
q[++r]=S;vis[S]=1;
while(++l<=r)
{
int x=q[l];
go(x)
{
if(vis[tn]||!e[i])continue;
vis[tn]=vis[x]+1;
if(tn==T)return 1;
q[++r]=tn;
}
}
return 0;
}
inline int dinic(int x,int flow)
{
if(x==T)return flow;
int res=flow,k;
for(int i=cur[x];i&&res;i=nex[i])
{
cur[x]=i;
int tn=ver[i];
if(vis[tn]==vis[x]+1&&e[i])
{
k=dinic(tn,min(e[i],res));
if(!k){vis[tn]=0;continue;}
res-=k;e[i^1]+=k;e[i]-=k;
}
}
return flow-res;
}
int main()
{
freopen("1.in","r",stdin);
gt(TT);
while(TT--)
{
gt(n);gc(a);ans=0;len=1;
memset(lin,0,sizeof(lin));
rep(0,9,i)gt(s1[i]),gt(s2[i]);
rep(1,n,i)rep(1,n,j){gt(b[i][j]);if(i==j)b[i][j]=0;}
cnt=n*n;S=++cnt;T=++cnt;
rep(1,n,i)w[i]=++cnt;rep(0,9,i)c[i]=++cnt;
rep(1,n,i)rep(1,n,j)
{
ans+=b[i][j];
int ww=(i-1)*n+j;
if(b[i][j])add(S,ww,b[i][j]);
add(ww,w[i],INF);
add(ww,w[j],INF);
}
rep(1,n,i)
{
int cc=a[i]-'0';
if(s1[cc])add(w[i],T,s1[cc]);
add(w[i],c[cc],INF);
}
rep(0,9,i)if(s1[i]-s2[i]<0)add(c[i],T,-s1[i]+s2[i]);
int sum=0,flow;
while(bfs())while((flow=dinic(S,INF)))sum+=flow;
put(ans-sum);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号