4.15 省选模拟赛 哈密顿回路 折半搜索 双指针

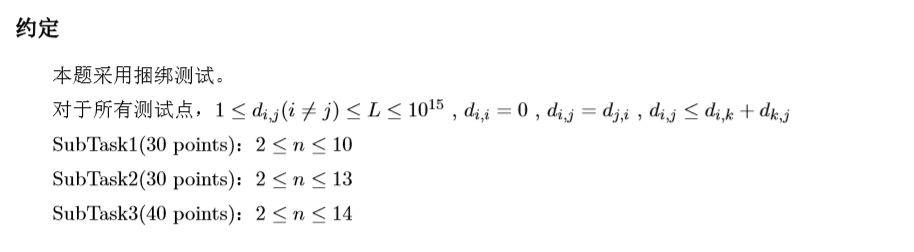
看一眼题目 显然点的状态之间合并也没用 所以状压dp就不行了。

观察点数 很少 但是边数很多 还是考虑爆搜点数。

容易获得 30分的阶乘搜索。

其实很容易发现这个可以使用折半搜索来优化。

不过考试的时候 想了一个非常麻烦的折半搜索 所以GG.

原来的思路：由于一定形成回路 那么 可以先2^n枚举其中的集合 然后爆搜出所有的路径。

对于另一半也同理 合并的时候采用二分处理。

不过考试的时候 由于睡了2h 没时间了 所以没细想。

现在想想当时2^n枚举其中集合是没必要的做法。

首先 我们搜一半再拼接肯定是比较优的。

考虑直接搜一半 考虑起点 因为是回路所以从1开始也行。搜到一半就停止 然后 放到vector里或者map里来进行两端对接。

考虑对接的时候 如果我们知道某个路径的终点 和起点 加上边权即可。

不过这样在对接的时候还得暴力枚举。

考虑直接在搜的时候 同一个起点开始也让他们同一个终点结束 这样只要中间的集合不同这样我们就可以直接对接起来。

对接建议使用sort+双指针这样常数比较小。

注意 搜前一半和后一半的点数要计算准确。

复杂度 可以发现 设一半点数为 w,那么搜索的状态总数为 C(n,w)*w!=1e7左右 加上sort是分部的 实际上加上一些剪枝还是可以过的。

const int MAXN=15;
int n,la,lb;ll L;
ll a[MAXN][MAXN];
vector<ll>g[MAXN][1<<MAXN];
inline void dfs(int x,int w,int s,ll v)
{
	if(v>L)return;
	if((w==la+1)||(w==lb+1))g[x][s].pb(v);
	if(w==la+1)return;
	rep(1,n,i)
	{
		if(s&(1<<(i-1)))continue;
		int ww=s|(1<<(i-1));
		dfs(i,w+1,ww,v+a[x][i]);
	}
}
int main()
{
		freopen("hamilton.in","r",stdin);
	freopen("hamilton.out","w",stdout);
	get(n);get(L);
	rep(1,n,i)rep(1,n,j)get(a[i][j]);
	//putl(a[1][2]);
	la=(n)/2;
	lb=(n)-la;
	if(la<lb)swap(la,lb);
	//put(la);put(lb);
	dfs(1,1,1,0);
	//putl(L);put(la);put(lb);
	int maxx=(1<<(n))-1;
	rep(1,n,i)rep(1,maxx,j)
	if(g[i][j].size())sort(g[i][j].begin(),g[i][j].end());
	rep(1,n,i)
	{
		rep(1,maxx,j)
		{
			if(!(j&(1<<(i-1))))continue;
			int s=(j^maxx)|1|(1<<(i-1));
			int r=g[i][s].size()-1;
			for(ui l=0;l<g[i][j].size();++l)
			{
				while(r>=0&&g[i][j][l]+g[i][s][r]>L)--r;
				if(r<0)break;
				if(g[i][j][l]+g[i][s][r]==L){puts("possible");return 0;}
			}
		}
	}
	puts("impossible");
	return 0;
}