4.11 省选模拟赛 序列 二分 线段树优化dp set优化dp 缩点

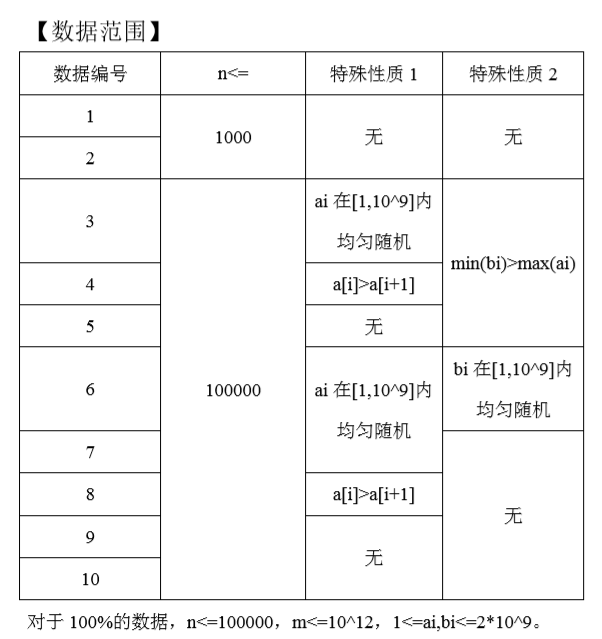
容易想到二分。

看到第一个条件容易想到缩点。

第二个条件自然是分段 然后让总和最小 容易想到dp.

缩点为先：我是采用了取了一个前缀最小值数组 二分+并查集缩点 当然也是可以直接采用 其他的奇奇怪怪的做法。

二分为重 发现变成了dp使得总a值尽可能小的问题。

方程为 f[i]=min(f[j]+max(j+1~i)a[k]); 这个问题容易使用线段树优化dp来解决。

单调栈维护决策区间修改即可。不过被卡常了 只有90points

const int MAXN=100010;
ll n,m,top,cnt,num;
ll b[MAXN],sum[MAXN],c[MAXN],fa[MAXN];
ll B[MAXN],L,R,s[MAXN],f[MAXN],w[MAXN],a[MAXN],A[MAXN];
struct jl{int l,r,id;ll sum;}g[MAXN<<2];
struct wy{int l,r;ll sum,tag;}t[MAXN<<2];
inline int getfather(int x){return x==fa[x]?x:fa[x]=getfather(fa[x]);}
inline void build(int p,int l,int r)
{
	l(p)=l;r(p)=r;
	if(l==r)return;
	int mid=(l+r)>>1;
	build(zz,l,mid);
	build(yy,mid+1,r);
}
inline void pushdown(int p)
{
	tag(zz)+=tag(p);
	tag(yy)+=tag(p);
	sum(zz)+=tag(p);
	sum(yy)+=tag(p);
	tag(p)=0;return;
}
inline void modify(int p,int x,ll w)
{
	if(l(p)==r(p)){sum(p)=w;return;}
	int mid=(l(p)+r(p))>>1;
	if(tag(p))pushdown(p);
	if(x<=mid)modify(zz,x,w);
	else modify(yy,x,w);
	sum(p)=min(sum(zz),sum(yy));
}
inline void cle(int p)
{
	sum(p)=inf;tag(p)=0;
	if(l(p)==r(p))return;
	cle(zz);cle(yy);
}
inline void change(int p,int l,int r,ll x)
{
	if(l<=l(p)&&r>=r(p))
	{
		sum(p)+=x;
		tag(p)+=x;
		return;
	}
	int mid=(l(p)+r(p))>>1;
	if(tag(p))pushdown(p);
	if(l<=mid)change(zz,l,r,x);
	if(r>mid)change(yy,l,r,x);
	sum(p)=min(sum(zz),sum(yy));
}
inline ll ask(int p,int l,int r)
{
	if(l<=l(p)&&r>=r(p))return sum(p);
	int mid=(l(p)+r(p))>>1;
	ll cnt=inf;if(tag(p))pushdown(p);
	if(l<=mid)cnt=min(cnt,ask(zz,l,r));
	if(r>mid)cnt=min(cnt,ask(yy,l,r));
	return cnt;
}
inline int check(ll x)//每一段的B的和都要<=mid
{
	cle(1);
	modify(1,0,0);
	int flag=1,l=0;
	rep(1,cnt,i)
	{
		while(flag<=num&&g[flag].id==i)
		{
			change(1,g[flag].l,g[flag].r,g[flag].sum);
			++flag;
		}
		while(w[i]-w[l]>x)++l;
		f[i]=ask(1,l,i-1);
		modify(1,i,f[i]);
	}
	return f[cnt]<=m;
}
signed main()
{
	freopen("sequence.in","r",stdin);
	freopen("sequence.out","w",stdout);
	get(n);get(m);sum[0]=INF;
	rep(1,n,i)
	{
		get(a[i]);get(b[i]);fa[i]=i;
		sum[i]=min(b[i],sum[i-1]);
	}
	rep(1,n,i)
	{
		if(sum[i-1]>a[i])continue;
		int l=1,r=i-1;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(sum[mid]<=a[i])r=mid;
			else l=mid+1;
		}
		//r为不合法左端点.
		int w=i;
		while(w>r)
		{
			int cc=getfather(w-1);
			fa[w]=cc;w=cc;
		}
	}
	rep(1,n,i)
	{
		int xx=getfather(i);
		if(xx==i)
		{
			c[xx]=++cnt;
			A[cnt]=a[i];
			B[cnt]+=b[i];
		}
		else
		{
			A[c[xx]]=max(A[c[xx]],a[i]);
			B[c[xx]]+=b[i];
		}
		L=max(L,B[c[xx]]);
	}
	rep(1,cnt,i)
	{
		w[i]=w[i-1]+B[i];
		g[++num]=(jl){i-1,i-1,i,A[i]};
		int last=i-1;
		while(top&&A[i]>=A[s[top]])
		{
			g[++num]=(jl){s[top-1],last-1,i,A[i]-A[s[top]]};
			last=s[top-1];--top;
		}
		s[++top]=i;
	}
	build(1,0,cnt);
	R=w[cnt];
	while(L<R)
	{
		ll mid=(L+R)>>1;
		if(check(mid))R=mid;
		else L=mid+1;
	}
	putl(L);return 0;
}

考虑另外一种优化dp的方法。

set 因为fi<=fi+1 所以对于被同一个a值笼罩的一段最左端节点是最优的 单调队列维护每一个这样的左端点即可。

当然 还有一个最优决策的来源可能是 最左端能用的节点 set维护前者即可。

const int MAXN=100010;
ll m;int n,top,cnt,num;
int b[MAXN],sum[MAXN],c[MAXN],fa[MAXN];
ll B[MAXN],L,R,s[MAXN],f[MAXN],w[MAXN],a[MAXN],A[MAXN],q[MAXN];
inline int getfather(int x){return x==fa[x]?x:fa[x]=getfather(fa[x]);}
multiset<ll>ss;
multiset<ll>::iterator it;
inline int check(ll x)//每一段的B的和都要<=mid
{
	ss.clear();
	int l=1,r,g=0;
	rep(1,cnt,i)
	{
		while(l<=r&&(A[i]>=A[q[r]]))
		{
			if(l<r)it=ss.find(f[q[r-1]]+A[q[r]]),ss.erase(it);
			--r;
		}
		q[++r]=i;
		if(l<r)ss.insert(f[q[r-1]]+A[q[r]]);
		while(w[i]-w[g]>x)++g;
		while(q[l]<=g)
		{
			ss.erase(f[q[l]]+A[q[l+1]]);
			++l;
		} 
		f[i]=f[g]+A[q[l]];
		if(l<r)f[i]=min(f[i],*ss.begin());
	}
	return f[cnt]<=m;
}
signed main()
{
	freopen("sequence.in","r",stdin);
	freopen("sequence.out","w",stdout);
	get(n);scanf("%lld",&m);sum[0]=INF;
	rep(1,n,i)
	{
		get(a[i]);get(b[i]);fa[i]=i;
		sum[i]=min(b[i],sum[i-1]);
	}
	rep(1,n,i)
	{
		if(sum[i-1]>a[i])continue;
		int l=1,r=i-1;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(sum[mid]<=a[i])r=mid;
			else l=mid+1;
		}
		//r为不合法左端点.
		int w=i;
		while(w>r)
		{
			int cc=getfather(w-1);
			fa[w]=cc;w=cc;
		}
	}
	rep(1,n,i)
	{
		int xx=getfather(i);
		if(xx==i)
		{
			c[xx]=++cnt;
			A[cnt]=a[i];
			B[cnt]+=b[i];
		}
		else
		{
			A[c[xx]]=max(A[c[xx]],a[i]);
			B[c[xx]]+=b[i];
		}
		L=max(L,B[c[xx]]);
	}
	rep(1,cnt,i)w[i]=w[i-1]+B[i];
	R=w[cnt];A[0]=inf;
	while(L<R)
	{
		ll mid=(L+R)>>1;
		if(check(mid))R=mid;
		else L=mid+1;
	}
	putl(L);return 0;
}