ZROI 提高十连测 DAY2
总结:入题尽量快,想到做法要先证明是否正确是否有不合法的情况,是否和题目中描述的情景一模一样。
不要慌 反正慌也拿不了多少分,多分析题目的性质如果不把题目的性质分析出来的话,暴力也非常的难写,有的时候甚至不写暴力更好,可能暴力代码难度过高且不易调出。
注意证明算法的正确性和复杂度不要盲目去刚去码,把所有情况都考虑清楚了,把可能会发生的情况也考虑进去,tink twice code once.
LINK :因为死刚题,没检查丢50,暴力没写对丢20,所以爆零且后悔莫及的一场比赛。
T1 感觉非常不可做,但是其实还行吧 没有仔细思考。
首先 有这样的一个问题问一个字符串是否在另一个字符串中出现过,这里是指下标可能不连续但是是递增的...
如何判断?我们知道可能解有很多个 而且我们也不知道取哪一个且这一类问题还有其他拓展我想到CF的一道题当时没有写现在来补上吧。
LINK:remove the substring
求 一个字符串中去掉最长的连续子串 还存在另一个字符串... 这都是对等位置的应用。n<=200显然暴力可过Y
发现 答案具有单调性 二分一下枚举从哪个地方断开再暴力判断 n^2logn 很稳...

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<ctime> #include<cstring> #include<string> #include<ctime> #include<cctype> #include<cstdio> #include<utility> #include<queue> #include<stack> #include<deque> #include<map> #include<set> #include<bitset> #include<vector> #include<algorithm> #include<cstdlib> using namespace std; const int MAXN=200010; int n,m; char s[MAXN],w[MAXN]; inline int check(int x) { for(int i=1;i<=n-x+1;++i)//区间的起点 { int j=i+x-1;//终点 int cnt=1; for(int k=1;k<=n;++k) { if(k>=i&&k<=j)continue; if(s[k]==w[cnt]) { ++cnt; if(cnt==m+1)return 1; } } } return 0; } int main() { //freopen("1.in","r",stdin); scanf("%s",s+1);n=strlen(s+1); scanf("%s",w+1);m=strlen(w+1); int l=0,r=n; while(l+1<r) { int mid=(l+r)>>1; if(check(mid))l=mid; else r=mid; } if(check(r))printf("%d\n",r); else printf("%d\n",l); return 0; }
LINK:加强版.
当n是200000的时候 上面的方法行不通了我们只能通过研究性质 使用nlogn的或者 O(n)的做法.(这是我们需要研究这个一个字符串在另一个字符串中出现过的性质...
考虑上面的那个匹配的做法 我们最后得到的无非是一个字典序最小的下标 。如果说 只有一个合法的匹配显然答案很好找。
设在文本字符串中匹配的字符下标为 p1,p2...pm 这个是字典序最小的 答案为 max(p1-1,p2-p1-1,...,n-pm);但是这个p数组不固定怎么办?
我们考虑 优化二分check的过程 在check之中我们枚举断点在哪然后判断这个东西之后还能否拼出 这个这两个点为 l r 我们可以预处理出到达l所能拼的最大长度f[l] 还有一个从后往前匹配到达r能拼的最大长度g[r]
显然 f[l]+g[r] >=m那么就合法 复杂度nlogn。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<ctime> #include<cstring> #include<string> #include<ctime> #include<cctype> #include<cstdio> #include<utility> #include<queue> #include<stack> #include<deque> #include<map> #include<set> #include<bitset> #include<vector> #include<algorithm> #include<cstdlib> using namespace std; const int MAXN=200010; int n,m; int f[MAXN],g[MAXN]; char s[MAXN],w[MAXN]; inline int check(int x) { for(int i=1;i<=n-x+1;++i)//区间的起点 { int j=i+x-1;//终点 if(f[i-1]+g[j+1]>=m)return 1; } return 0; } int main() { //freopen("1.in","r",stdin); scanf("%s",s+1);n=strlen(s+1); scanf("%s",w+1);m=strlen(w+1); int flag=1; for(int i=1;i<=n;++i) { f[i]=f[i-1]; if(w[flag]==s[i]&&flag<=m) { ++flag; ++f[i]; } } flag=m; for(int i=n;i;--i) { g[i]=g[i+1]; if(flag&&w[flag]==s[i]) { --flag; ++g[i]; } } int l=0,r=n; while(l+1<r) { int mid=(l+r)>>1; if(check(mid))l=mid; else r=mid; } if(check(r))printf("%d\n",r); else printf("%d\n",l); return 0; }
当然 题解中的做法是 O(n)的 想办法将这个搞出来 再次考虑刚才的check的过程 我们发现 答案所在点必然在一个点是正向匹配点一个点是是反向匹配点,也就是说我们只要给正向匹配点找一个最大的反向匹配点即可。
这样统计答案 就少去了二分的过程了 如何进行匹配?观察我们正向匹配点是连续的一段,所以随着正向匹配点的向右推进反向匹配点也同时可以向右推进 维护两个指针扫一下即可 复杂度O(n);

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<ctime> #include<cstring> #include<string> #include<ctime> #include<cctype> #include<cstdio> #include<utility> #include<queue> #include<stack> #include<deque> #include<map> #include<set> #include<bitset> #include<vector> #include<algorithm> #include<cstdlib> using namespace std; const int MAXN=200010; int n,m,ans; int f[MAXN],g[MAXN]; char s[MAXN],w[MAXN]; int main() { freopen("1.in","r",stdin); scanf("%s",s+1);n=strlen(s+1); scanf("%s",w+1);m=strlen(w+1); int flag=1; for(int i=1;i<=n;++i) { f[i]=f[i-1]; if(w[flag]==s[i]&&flag<=m) { ++flag; ++f[i]; } } flag=m; for(int i=n;i;--i) { g[i]=g[i+1]; if(flag&&w[flag]==s[i]) { --flag; ++g[i]; } } for(int i=0,j=1;i<=n;++i) { while(f[i]+g[j+1]>=m&&j<=n)++j; ans=max(ans,j-i-1); } printf("%d\n",ans); return 0; }
发现是一道水题...但是 这也是思维的渐进性...由此我们做题的时候 也需要这样的渐进性 而不是一蹴而就(神仙除外...
正式的开始我们的T1 一个好的序列我们显然可以通过刚才的做法随便求出且这样做求出的一个好的下标序列字典序是最小的。先设出这个最小字典序的东西是集合{p1,p2,p3...pm};
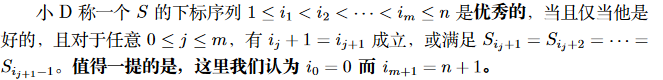
这个是题目的要求 是指两个p必须是连续的或者两个p之间所有的字母都相同。如何对这两个条件同时进行归纳显得尤为重要。
我们将p可以映射到S上 也就是相邻的p要么是连续的要么之间所有的字母都相同这样在S中我们把当前位如何和下一位不相等我们就给标记出来 最后发现如果对于两个相邻的被标记的点我们至少有一个是p的话那么这就是符合答案的。当然边界我们先不考虑。
现在 我们求出了p了我们只需要把p放在刚刚的i 或i+1上即可 对于每一个 i 或 i+1 必然得放一个 不可以不放因为如果两个都不放的话那么必然是不合法的 所以我们只需要对着i和i+1找p即可。注意到要找最大的j如果找一个较小的j我们后面还要插入多个j的话 那么j的个数越多越好,所以要找最大的j 如果不存在 因为我们是字典序最小的 所以 对于任意一个序列 都是不存在的。大体上就是这样了 理解还是不深刻以后要复习。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<ctime> #include<cstring> #include<string> #include<ctime> #include<cctype> #include<cstdio> #include<utility> #include<queue> #include<stack> #include<deque> #include<map> #include<set> #include<bitset> #include<vector> #include<algorithm> #include<cstdlib> using namespace std; const int MAXN=300010; int n,m,ans; int p[MAXN]; char a[MAXN],b[MAXN]; int main() { //freopen("1.in","r",stdin); scanf("%d",&n);scanf("%d",&m); scanf("%s",a+1);scanf("%s",b+1); int flag=1; for(int i=1;i<=m;++i,++flag) { while(flag<=n&&a[flag]!=b[i])++flag; if(flag<=n)p[i]=flag; } if(!p[m]){puts("-1");return 0;} flag=m; for(int i=n;i>=2;--i) { if(a[i]==a[i-1])continue; while(p[flag]>i&&flag>=1)--flag; if(!flag){puts("-1");return 0;} if(p[flag]==i-1||p[flag]==i)continue; if(b[flag]==a[i])p[flag]=i; else p[flag]=i-1; } for(int i=1;i<=m;++i)printf("%d ",p[i]); return 0; }
T2 相当的 有趣 反正我都没推出来。
求最长的宽窄路连续个数最小,貌似很难写的样子,显然一点是二分 。(现在二分用的非常之多...
想的时候脑抽了 以为无环 那我倒着dp一下就好了码码码 发现topsort写完之际想到了有环怎么办,看了一眼题目发现样例都有环 删删删 有点慌、
突然想到了 直接暴力好了 dp f[i][j][p] 表示当前到达i这个点连续的p类路为长度为j是否可行 发现转移到这个状态还不够一条路径上的其他的信息也是需要判断是否合法 于是还是二分。
发现>mid的时候直接减掉就好了,然后一转移 n^2logn相当的稳... 50分到手(其实当时没发觉>mid写成>=mid 状态转移也写错了一点 然后还能过样例...flag每次也没清0 2333...总之爆零

//#include<bits/stdc++.h> #include<iostream> #include<cmath> #include<ctime> #include<algorithm> #include<cctype> #include<utility> #include<queue> #include<map> #include<set> #include<bitset> #include<deque> #include<vector> #include<cstdio> #include<cstdlib> #include<iomanip> #include<stack> #include<string> #include<cstring> #define INF 1000000000 #define ll long long #define db double #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define mp(x,y) make_pair((x),(y)) using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return f<0?-x:x; } const int MAXN=510; int n,len; int vis[MAXN],mid,flag; int f[MAXN][MAXN][2]; int lin[MAXN],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline void dfs(int x) { vis[x]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn])continue; dfs(tn); } } inline void dp(int x,int w,int p) { if(flag)return; if(w>mid)return; if(x==1){flag=1;return;} if(f[x][w][p])return; f[x][w][p]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(flag)return; dp(tn,p==e[i]?w+1:1,p==e[i]?p:p^1); } } int main() { //freopen("1.in","r",stdin); n=read(); if(n<=500) { for(int i=1;i<=n;++i) { int x,y; x=read();y=read(); add(x,i,0); add(y,i,1); } dfs(n); if(!vis[1]){puts("-1");return 0;} int l=1,r=n; while(l<r) { flag=0; memset(f,0,sizeof(f)); mid=(l+r)>>1; dp(n,0,0); dp(n,0,1); if(flag)r=mid; else l=mid+1; } printf("%d\n",r); } else puts("-1"); return 0; }
想一下正解怎么做吧,我们发现二分出来之后某个点最多跑mid步宽路或者窄路。强制令其跑这么多或者不跑这么多 都必须得换边跑。这样我们只需要判断是否能跑到n即可 当然还是和上面的思路不尽相同。
我们考虑每次二分后重新生成一张图 然后 不跑f数组了 直接跑到某个点然后切换边 看最后能跑到n不能。这样复杂度还是n^2logn的,但是 我们可以有一种神奇的做法叫做倍增优化建图,然后点数和边数都是nlogn的 但是有近乎4倍的常数 且 dfs暴力每次都清理一些数组什么的太慢了 所以只能得到80 这还是在我的卡常情况之下 不卡的话只有50分。

//#include<bits/stdc++.h> #include<iostream> #include<cmath> #include<ctime> #include<algorithm> #include<cctype> #include<utility> #include<queue> #include<map> #include<set> #include<bitset> #include<deque> #include<vector> #include<cstdio> #include<cstdlib> #include<iomanip> #include<stack> #include<string> #include<cstring> #define INF 2000000000 #define ll long long #define db double #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define mp(x,y) make_pair((x),(y)) #define R register using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return f<0?-x:x; } const int MAXN=200010,T=18; int n,cnt,len1,len; int vis[MAXN*T<<2][2],mark[MAXN]; int lin[MAXN*T<<2],nex[MAXN*T<<2],ver[MAXN*T<<2],e[MAXN*T<<2]; int f[MAXN][19][2],num[MAXN][19][2],pos[1<<19]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline void dfs(int x,int p) { vis[x][p]=1; for(R int i=lin[x];i;i=nex[i]) { R int tn=ver[i]; if(x<=n&&e[i]==p)continue; if(vis[tn][e[i]])continue; dfs(tn,e[i]); } } inline int check(int x) { for(R int i=1;i<=cnt;++i) { if(i<=n)lin[i]=0; vis[i][0]=vis[i][1]=0; } len=len1; for(R int i=1;i<=n;++i) { R int y=i,h=i,s=x,last=x; while(s) { s-=s&(-s); int w=last-s,j=pos[w]; add(i,num[y][j][0],0); add(i,num[h][j][1],1); y=f[y][j][0]; h=f[h][j][1]; last=s; } } dfs(1,0); dfs(1,1); if(vis[n][0]||vis[n][1])return 1; return 0; } inline void dp(int x) { mark[x]=1; int tn=f[x][0][0]; int tn1=f[x][0][1]; if(!mark[tn])dp(tn); if(!mark[tn1])dp(tn1); } int main() { //freopen("1.in","r",stdin); n=read();cnt=n; for(int i=0;i<=T;++i)pos[1<<i]=i; for(int i=1;i<=n;++i) { int x,y; x=read();y=read(); f[i][0][0]=x; f[i][0][1]=y; num[i][0][0]=x; num[i][0][1]=y; } dp(1); if(!mark[n]){puts("-1");return 0;} for(int i=1;i<=T;++i) for(int j=1;j<=n;++j) { num[j][i][1]=++cnt;num[j][i][0]=++cnt; f[j][i][0]=f[f[j][i-1][0]][i-1][0]; f[j][i][1]=f[f[j][i-1][1]][i-1][1]; add(num[j][i][0],num[j][i-1][0],0); add(num[j][i][0],num[f[j][i-1][0]][i-1][0],0); add(num[j][i][1],num[j][i-1][1],1); add(num[j][i][1],num[f[j][i-1][1]][i-1][1],1); } len1=len; int l=1,r=n; while(l<r) { int mid=(l+r)>>1; if(check(mid))r=mid; else l=mid+1; } printf("%d\n",r); return 0; }
好自闭Y 写不动了 这题太鬼畜了 题解看不懂 好难受 啊...
照着别人的抄了一遍 理解不了 明天中午再说:

//#include<bits/stdc++.h> #include<iostream> #include<cmath> #include<ctime> #include<algorithm> #include<cctype> #include<utility> #include<queue> #include<map> #include<set> #include<bitset> #include<deque> #include<vector> #include<cstdio> #include<cstdlib> #include<iomanip> #include<stack> #include<string> #include<cstring> #define INF 2000000000 #define ll long long #define db double #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define mp(x,y) make_pair((x),(y)) using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return f<0?-x:x; } const int MAXN=200010,T=18; int n; queue<pair<int,int> > q; int a[MAXN][2],mark[MAXN],f[MAXN][2],d[MAXN][2],vis[MAXN][2]; inline void dfs(int x) { mark[x]=1; if(!mark[a[x][0]])dfs(a[x][0]); if(!mark[a[x][1]])dfs(a[x][1]); } inline int getfather(int x,int p) { if(f[x][p]==x)return x; int fa=getfather(f[x][p],p); d[x][p]+=d[f[x][p]][p];f[x][p]=fa; return fa; } inline int check(int k) { memset(vis,0,sizeof(vis)); for(int i=1;i<=n;++i)f[i][0]=f[i][1]=i,d[i][0]=d[i][1]=0; vis[1][0]=1;vis[1][1]=1; q.push(mp(1,0));q.push(mp(1,1)); while(q.size()) { int x=q.front().first; int p=q.front().second; q.pop(); x=a[x][p];int y=x; while(1) { y=getfather(y,p); if(vis[y][p^1])break; getfather(x,p); if(d[x][p]>=k)break; vis[y][p^1]=1; q.push(mp(y,p^1)); if(getfather(a[y][p],p)==y)break; f[y][p]=a[y][p];++d[y][p]; } } if(vis[n][0]||vis[n][1])return 1; return 0; } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;++i) { int x,y; x=read();y=read(); a[i][0]=x;a[i][1]=y; } dfs(1); if(!mark[n]){puts("-1");return 0;} int l=0,r=n; while(l<r) { int mid=(l+r)>>1; if(check(mid))r=mid; else l=mid+1; } printf("%d\n",r); return 0; }
然后 上述代码被我不知不觉给咕了 但是 改还是得改的 物理 学的觉得不太对劲了,越学越迷 我应该试着去总结什么 啊 快考试了 自闭算了...
T3 看起来很难搞得样子 其实真的挺难搞 的,我初次观察是发现了 答案具有单调性不妨二分答案,然后只要判断在这个答案范围内都是合法的即可。发现很难因为长度为mid的且经过两点x y的路径有很多 当时感觉能拿20 最后还是写爆了 情况过多 无力回天。
应该要想到转换问题的 求最小的l使得每一条简单路径上GCD为1 也就是求出最大的不合法路径l 答案就是l+1了...这个有什么好处 我们再次分析这个最大的l 发现在这个最大l中必然GCD不为1 那么 GCD中必然含有某个质因数 所以呢 其实答案就是从x点出发的最长的含这个质因数的路径+从y出发的这个质因数的路径 + dis x,y 直接求最长路径无疑直接dfs即可 刚好 边权<=1e6 撑死7个质因数我们暴力枚举 然后 暴力的找答案 即可 这样的话我们就很好写了复杂度 qn这样就有50分的好成绩了 如果求两点之间的GCD采用倍增的话 说不定可以水过这道题...但是 不知道为什么我哪里写挂了一直T /ll 正解是这样的 我们继续优化这个算法 发现每条边最多被经过7次 我们可以统计一下这个点以这个质因数为导引的最长路径这样每次调用就方便很多了...
我们进行这个预处理也是 最多7n的复杂度 不过感觉有点难写因为存在最长路可能是在y上的 所以还要存次长路什么的,具体做法就是这样了 。问题的关键,学会转换问题。
终于在我坚持不懈的 努力之下 调了出来 宏定义的锅 上次就是这个让我线段树一直T 这次还是这玩意。made 容我自己骂自己一会...
发现暴力做法可过 我在考虑写不写正解呢,衡量之下 我觉定这里再次声明一点 宏定义min max 切记不能使用在套dfs或者线段树的ask中 会T到你怀疑人生 怀疑你是不是就是一个bug。
再次思索了一下还是不写了因为这个代码难度较高且实现不易,况且还有可能 过多的使用STL加慢速度 故 不建议写(原因是快月考了 感觉学习。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 2147483646 #define ll long long #define R register using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } const int MAXN=200010; int n,Q,G,len,maxx; vector<int>v[1000010]; int Log[MAXN],p[1000010]; int f[MAXN][20],g[MAXN][20],d[MAXN],fu,fv; int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1]; inline void swap(int &x,int &y){int tmp=x;x=y;y=tmp;} inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline int gcd(int a,int b){return b?gcd(b,a%b):a;} inline void dfs(int x,int father) { d[x]=d[father]+1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; f[tn][0]=x;g[tn][0]=e[i]; for(int j=1;j<=Log[n];++j) { f[tn][j]=f[f[tn][j-1]][j-1]; g[tn][j]=gcd(g[f[tn][j-1]][j-1],g[tn][j-1]); } dfs(tn,x); } } inline int LCA(int x,int y) { if(d[x]<d[y])swap(x,y); for(int i=Log[d[x]];i>=0;--i) if(d[f[x][i]]>=d[y]) { G=gcd(G,g[x][i]); x=f[x][i]; } if(x==y)return x; for(int i=Log[d[x]];i>=0;--i) if(f[x][i]!=f[y][i]) { G=gcd(G,g[x][i]); G=gcd(G,g[y][i]); x=f[x][i]; y=f[y][i]; } G=gcd(G,g[x][0]); G=gcd(G,g[y][0]); return f[x][0]; } inline int getx(int x,int w) { for(int i=Log[n];i>=0;--i) if(w&(1<<i))x=f[x][i]; return x; } inline int get_dis(int x,int father,int g) { int d=0; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; if(e[i]%g==0)d=max(d,get_dis(tn,x,g)+1); } return d; } inline int get_d(int x,int father) { int d=0; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; d=max(d,get_d(tn,x)+1); } return d; } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();Q=read(); for(int i=2;i<=n;++i) { int x,y,z; x=read();y=read();z=read(); add(x,y,z);add(y,x,z); maxx=max(maxx,z); Log[i]=Log[i>>1]+1; } dfs(1,0); for(R int i=2;i<=1000000;++i) { if(p[i])continue; for(R int j=i;j<=1000000;j=j+i) v[j].push_back(i),p[j]=1; } //G=90;for(unsigned int i=0;i<v[G].size();++i)cout<<v[G][i]<<endl; while(Q--) { int x,y,lca,dis;G=0; x=read();y=read(); lca=LCA(x,y); dis=d[x]+d[y]-d[lca]-d[lca]; if(G==1){printf("%d\n",dis);continue;} if(lca==x){fu=getx(y,dis-1);fv=f[y][0];} if(lca==y){fv=getx(x,dis-1);fu=f[x][0];} if(lca!=x&&lca!=y){fu=f[x][0];fv=f[y][0];} int cnt=get_d(x,fu)+get_d(y,fv); int ans=0; for(R unsigned int i=0;i<v[G].size();++i) { //cout<<v[G][i]<<endl; int w1=get_dis(x,fu,v[G][i]); int w2=get_dis(y,fv,v[G][i]); ans=max(ans,w1+w2); } if(ans==cnt){puts("-1");continue;} printf("%d\n",ans+dis+1); } return 0; }
好了 这次考试 就告一段落了 要注意 考试的总结 和下次应该做的事情才是明智的。智者 从不犯相同的第二次错误。
update by 2019 9 14:竟然考后hack 服了 还得再debug 其中第二题和第三题都被hack掉了,这是很严重的问题。当然 其中T3 做法有点假。
T2 发现 n可以等于 1 那么输入就是 1 1 1 这样答案就是0 应该不用动就到了终点 这是关于二分的上下界的问题 这里 我再次理解一下冰茶集的做法。(code100分的改过了其他的懒得改...
具体的此题冰茶集是这样写的 类似于倍增优化建图我们钦定每到达一个点就立刻换向 最后检查整张图的连通性 不妨我们直接冰茶集来做这个事情。判断连通性冰茶集很容易就能搞出来了...
如何 来搞这个东西 二分之后首先我们先把1 0 和1 1 加入队列中来实现对整张图的遍历 用路径压缩来遍历整张图。我觉得 没有倍增优化建图简单 获知树链剖分 +线段树优化建图但这样要复杂一点。
T3 发现做法是假的 复杂的是nq的 这是复杂度极不科学 却被我水过...这里考虑优化我们发现每条边的质因子数最多有7个每条边最多经过7次 考虑记忆化 或者存map。
我觉得需要存次长和最长 所以考虑开vector搞吧 这样预处理是7n的应该 这样询问的时候应该可以是O(Q)的。发现不太好搞因为 我们从点开始预处理是不知道哪个质因子的 所以我们可以从边开始 但是这样做非常的复杂 所以考虑 直接询问的时候搞 开map存无疑是最优秀的做法。发现map不太行...所以思考的时候 觉得可以实现的时候觉得不行,原因是 记忆化如果跑的是x 到y的那条路径的最长链怎么办?最长和次长map 只能有一个关键字加上质因数p 我们已经是map套map了次长必然维护不了 暴力的话 复杂度就不正确了。vector倒是可以搞但是 还是会出现上述我们不知道质因数是哪一个的问题..况且找的时候 复杂度估计也不大正确 map是必要的...但是解决不了次长 。这种思路结束。
问了一个dalao 正确做法是离线搞 对于某个质因子我们把图生成出来不过最终的图的大小和累计是7n所以复杂度是正确的 考虑对于没一张图我们对于某个点都求出最长和次长 这样就解决了问题不需要记忆化 直接一起处理就好了很多。
代码 回来补坑。
update 9 16 又考了很多考试但是ZR的题相当的不错我还是决定每场比赛都要总结 于是 写了2h这个代码 比较难调,大概的思路就是上面的离线。
注意 求 过两点的最长链和次长链 有方法的 开数组 m1 m2 h 分别表示 子树内的最长链 次长链向上的最长链 然后 根据LCA合理判断一下即可。
代码 很难写 有点复杂 题目非常的有意思。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 1000000001 #define ll long long #define R register #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int MAXN=200010,maxn=1000010; int n,Q,maxx=1000000,top,len,gg; int vis[maxn],w[maxn],d[MAXN],Log[MAXN]; int f[MAXN][20],g[MAXN][20],m1[MAXN],m2[MAXN],h[MAXN]; int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1]; vector<int>p[maxn],v[maxn],G[maxn],V[maxn]; struct wy { int x,y,lca; int G,ans,maxx,last; }t[MAXN]; inline int gcd(int a,int b){return b?gcd(b,a%b):a;} inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline void dfs(int x,int father) { d[x]=d[father]+1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; g[tn][0]=e[i]; f[tn][0]=x; for(int j=1;j<=Log[d[x]];++j) { f[tn][j]=f[f[tn][j-1]][j-1]; g[tn][j]=gcd(g[tn][j-1],g[f[tn][j-1]][j-1]); } dfs(tn,x); } } inline int LCA(int x,int y) { gg=0; for(int i=Log[d[y]];i>=0;--i) if(d[f[y][i]]>=d[x]) { gg=gcd(gg,g[y][i]); y=f[y][i]; } if(x==y)return x; for(int i=Log[d[x]];i>=0;--i) { if(f[x][i]!=f[y][i]) { gg=gcd(gg,g[x][i]); gg=gcd(gg,g[y][i]); x=f[x][i];y=f[y][i]; } } gg=gcd(gg,g[x][0]); gg=gcd(gg,g[y][0]); return f[x][0]; } inline void dp(int x,int father) { int mark=0; for(unsigned int i=0;i<V[x].size();++i) { int tn=V[x][i]; if(tn==father)continue; mark=1; dp(tn,x); int val=m1[tn]+1; if(val>m1[x])m2[x]=m1[x],m1[x]=val; else if(val>m2[x])m2[x]=val; } if(!mark)m1[x]=m2[x]=0; } inline void dp(int x,int father,int val) { h[x]=val; for(unsigned int i=0;i<V[x].size();++i) { int tn=V[x][i]; if(tn==father)continue; if(m1[tn]+1==m1[x]) dp(tn,x,max(val+1,m2[x]+1)); else dp(tn,x,max(val+1,m1[x]+1)); } } inline int get_x(int x,int d) { for(int i=Log[d];i>=0;--i) if(d&(1<<i))x=f[x][i]; return x; } inline int cmp(int x,int y){return d[x]<d[y];} int main() { //freopen("1.in","r",stdin); freopen("1.out","w",stdout); n=read();Q=read(); for(int i=2;i<=maxx;++i) { if(!vis[i]) { w[++top]=i; for(int j=i;j<=maxx;j+=i) { p[j].push_back(i); vis[j]=1; } } } for(int i=1;i<n;++i) { int x,y,z; x=read();y=read();z=read(); V[x].push_back(y); V[y].push_back(x); add(x,y,z);add(y,x,z); for(unsigned int j=0;j<p[z].size();++j) { int tn=p[z][j]; G[tn].push_back(x); G[tn].push_back(y); } } for(int i=2;i<=n;++i)Log[i]=Log[i>>1]+1; dfs(1,0); dp(1,0);dp(1,0,0); for(int i=1;i<=Q;++i) { int x,y; x=read();y=read(); //if(i==167)cout<<x<<' '<<y<<endl; if(d[x]>d[y])swap(x,y); t[i].x=x;t[i].y=y; t[i].lca=LCA(x,y); t[i].G=gg; //cout<<t[i].lca<<' '<<t[i].G<<endl; t[i].maxx=d[x]+d[y]-2*d[t[i].lca]; //cout<<t[i].maxx<<endl; if(t[i].lca==x) { t[i].last=get_x(t[i].y,d[t[i].y]-d[t[i].x]-1); //cout<<t[i].last<<endl; int ww=t[i].last; //if(i==4)cout<<t[i].maxx<<' '<<t[i].x<<' '<<t[i].y<<' '<<t[i].last<<' '<<m1[ww]<<' '<<m1[t[i].x]<<' '<<m2[t[i].x]<<' '<<m1[t[i].y]<<endl; /*if(i==4) { cout<<t[i].maxx<<endl; cout<<(m1[ww]+1==m1[t[i].x]?m2[t[i].x]:m1[t[i].x])<<endl; cout<<h[t[i].x]<<endl; }*/ //cout<<(m1[ww]+1==m1[t[i].x]?m2[t[i].x]:m1[t[i].x])<<' '<<h[t[i].x]<<' '<<m1[t[i].y]<<endl; t[i].maxx=t[i].maxx+max((m1[ww]+1==m1[t[i].x]?m2[t[i].x]:m1[t[i].x]),h[t[i].x])+m1[t[i].y]; //if(i==4)cout<<t[i].maxx<<endl; } else t[i].maxx+=m1[t[i].x]+m1[t[i].y]; //cout<<t[i].maxx<<endl; if(gg!=1) { for(unsigned int j=0;j<p[gg].size();++j) { int tn=p[gg][j]; v[tn].push_back(i); } } } //for(int i=1;i<=Q;++i)cout<<t[i].lca<<endl; //for(int i=1;i<=Q;++i)cout<<t[i].G<<endl; //for(int i=1;i<=Q;++i)cout<<t[i].maxx<<endl; for(int i=1;i<=n;++i) { V[i].clear(); m1[i]=m2[i]=-1; } for(int i=1;i<=top;++i)//对于每一个质因子都处理一遍 { //if(w[i]==2){cout<<"ww"<<endl;} if(!G[w[i]].size())continue; if(!v[w[i]].size())continue; for(unsigned int j=0;j<G[w[i]].size();j=j+2) { int tn=G[w[i]][j]; int ne=G[w[i]][j+1]; //if(w[i]==3)if(tn==100&&ne==35)cout<<"www"<<endl; V[tn].push_back(ne); V[ne].push_back(tn); } sort(G[w[i]].begin(),G[w[i]].end(),cmp); for(unsigned int j=0;j<G[w[i]].size();++j) { int tn=G[w[i]][j]; //if(w[i]==3)if(tn==100)cout<<"www"<<endl; if(m1[tn]==-1) { dp(tn,0); dp(tn,0,0); } } for(unsigned int j=0;j<v[w[i]].size();++j) { int tn=v[w[i]][j]; if(t[tn].lca==t[tn].x) { int ww=t[tn].last; //cout<<m1[ww]<<endl; int www=(m1[ww]+1==m1[t[tn].x]?m2[t[tn].x]:m1[t[tn].x]); //if(w[i]==3)cout<<www<<endl; www=max(www,h[t[tn].x]); t[tn].ans=max(t[tn].ans,www+m1[t[tn].y]); } else t[tn].ans=max(t[tn].ans,m1[t[tn].x]+m1[t[tn].y]); } for(unsigned int j=0;j<G[w[i]].size();j=j+2) { int tn=G[w[i]][j]; int ne=G[w[i]][j+1]; V[tn].clear(); V[ne].clear(); m1[tn]=m1[ne]=-1; h[tn]=m2[tn]=h[ne]=m2[ne]=0; } } for(int i=1;i<=Q;++i) { t[i].ans+=d[t[i].x]+d[t[i].y]-d[t[i].lca]*2; if(t[i].G==1){printf("%d\n",t[i].ans);continue;} if(t[i].ans==t[i].maxx)printf("%d\n",-1); else printf("%d\n",t[i].ans+1); } return 0; }
至此 这套题就结束了 还有下套题...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号