浅谈网络流
网络流我也学了一段时间了(不到一天)觉得是时候总结一下了。
做了一部分题目觉得非常的有意思但是对其理解仍是不深刻。。
首先就是EK算法了这个还比较简单明了 基于二分图的增广路找发bfs不断寻找增广路 增大网络中的流量来寻找最大流。
当然不太相同的地方自然是多了反向流 这个反向流其实是因为你把我的位置给占了你还有其他位置我可以通过你的反向流去跑你的路。
这就是 所谓的 : 走别人的路 让别人走投无路!。。还有一点是 这是每次求最短路的增广路 这是因为只有较长的路才会经常跑反向流所以为了优化是基于最短路增广路的。
也就是bfs 寻找增广路就好了。。EK 就这样完了 经常被卡 一般还是写dinic
dinic:我不会什么当前弧优化啊,不管好了以后再说。dinic还是不断的找增广路但是这个可以一次性更新多条增广路所以比EK要快一点。
分层图也很好理解 这就跟EK差不多而已,唯一注意的是代码中的一些剪枝 如rest==0了就停止 增广路更新完了就将其在图中删掉。
放几道很好的最大流的题目:

这道题 看起来是个树形dp 其实就是一个树形dp 同时还是一个最小割的模型。最大流==最小割。
我是这样理解的:证明的话想一下我们流向汇点的每条流的路径上必有一条路径是满流的,然后这些满流的加起来就是我们的最大流了,
自然把这些满流的删掉就是最小割了,如果不是那说明还具有增广路,由我们求最大流的时候把边都增广了,所以不存在这种情况,得证。
但是这道题很显然的是从源点到叶子节点增广路最多只有一条 所以跑一边dinic就是最大流了。。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 1000000000ll #define ll long long #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) #define RI register ll #define up(p,i,n) for(ll i=p;i<=n;++i) #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[20]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=200010; int n,s,len=1,t,h,flow,maxx; int d[MAXN],vis[MAXN],ru[MAXN]; int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline int dinic(int x,int flow) { if(x==n+1)return flow; int rest=flow,k;vis[x]=1; for(int i=lin[x];i&&rest;i=nex[i]) { int tn=ver[i]; if(!e[i]||vis[tn])continue; k=dinic(tn,min(rest,e[i])); e[i]-=k;rest-=k; } return flow-rest; } int main() { //freopen("1.in","r",stdin); n=read();s=read(); for(int i=1;i<n;++i) { int x,y,z; x=read();y=read();z=read(); add(x,y,z);add(y,x,z); ++ru[x];++ru[y]; } for(int i=1;i<=n;++i)if(i!=s&&ru[i]==1)add(i,n+1,INF); put(dinic(s,INF)); return 0; }
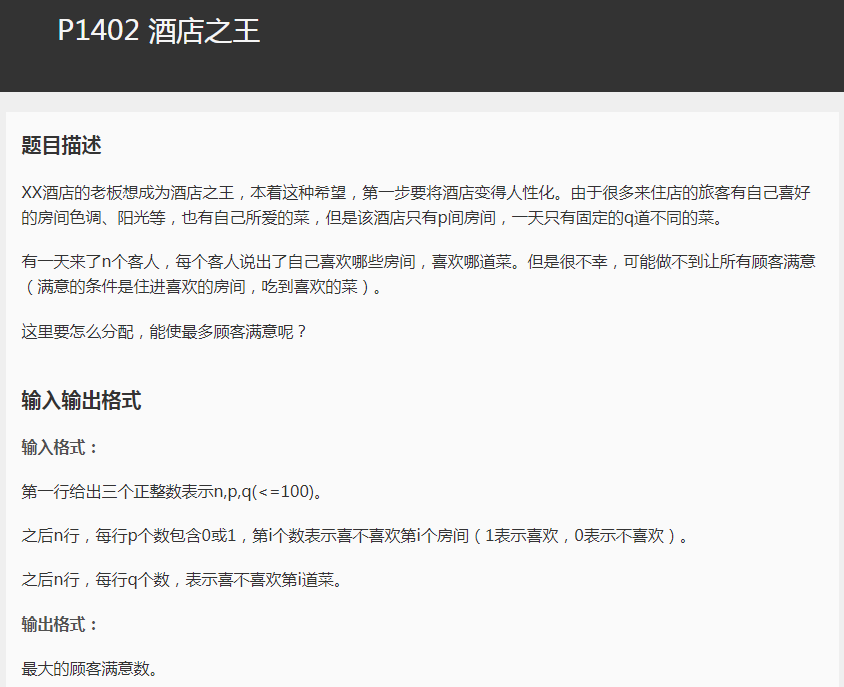
这道题写二分图的时候都想写这道题了,但是我仍然觉得二分图不太妥。网络流吧。
人 chose 菜 人 chose 房间 我首先想到的是 人连菜 菜连房间 事实上这样做是不对的 但是可以有一些做法使其变的正确。但是不妨转换一下。
菜连人 人连房间 这样做显然是更好写的 注意到这个地方人还是可能被用多次 所以拆点变边这样保证这条边的容量为1 所以就可以直接跑最大流了!

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 1000000000 #define ll long long #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) #define RI register ll #define up(p,i,n) for(ll i=p;i<=n;++i) #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[20]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50100; int n,p,Q,S,T,len=1,h,t,maxx; int vis[MAXN],q[MAXN]; int lin[MAXN],nex[MAXN],ver[MAXN],e[MAXN]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline int bfs() { memset(vis,0,sizeof(vis)); h=t=0;q[++t]=S;vis[S]=1; while(h++<t) { int x=q[h]; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(!e[i]||vis[tn])continue; vis[tn]=vis[x]+1; q[++t]=tn; if(tn==T)return 1; } } return 0; } inline int dinic(int x,int flow) { if(x==T)return flow; int rest=flow,k; for(int i=lin[x];i&&rest;i=nex[i]) { int tn=ver[i]; if(e[i]&&vis[tn]==vis[x]+1) { k=dinic(tn,min(e[i],rest)); if(!k)vis[tn]=0; e[i]-=k; e[i^1]+=k; rest-=k; } } return flow-rest; } int main() { //freopen("1.in","r",stdin); n=read();p=read();Q=read(); for(int i=1;i<=n;++i) for(int j=1;j<=p;++j) { if(!read())continue; add(i,(n<<1)+j,0);add((n<<1)+j,i,1); } for(int i=1;i<=n;++i)add(i,i+n,1),add(i+n,i,0); for(int i=1;i<=n;++i) for(int j=1;j<=Q;++j) { if(!read())continue; add(i+n,p+(n<<1)+j,1); add(p+(n<<1)+j,i+n,0); } S=(n<<1)+p+Q+1;T=S+1; for(int i=1;i<=p;++i)add(S,(n<<1)+i,1),add((n<<1)+i,S,0); for(int i=1;i<=Q;++i)add(i+(n<<1)+p,T,1),add(T,i+(n<<1)+p,0); int flow=0; while(bfs())while((flow=dinic(S,INF)))maxx+=flow; put(maxx); return 0; }

这道题是一个 非常难转换的最小割 至少 我全程懵逼。。最大流是求最小的吧 不然不会等于最小割。。那么全部剪掉就是最大值了。
先不考虑物品的组合 S像物品连线 物品向 A B连线 A B向汇点连线 那么此时我们发现 好些物品能选A 也能选择B 这个无妨 点边转换一下完成只能选择一个。
但是物品的组合呢?好像有点麻烦不会弃疗 。题解上是指S向物品连的这条边是指在A内部 物品向T连边是B那边 此时我们直接最小割 然后一减就是最大值啦。
考虑把组合放上去一个组合有效当且仅当这个组合和组合中的价值完全大于右边的东西。
然后这个东西其实是很难用语言来描述的 我简明的来说我们要构造出一个点让在这组有一个物品不选的时候 这组的全部价值就不能累加这一限制。
那么可以这样想如果对面有一个物品不选说明了此时对面的流量是一物品+组合的都比当前小 全删掉 那就是组合的这个东西给这组的所有物品进行支援。
建图时就和S相连再连向每一个这个组合的物品 对于B也同时如此 全部物品连向这个组合 这个组合连向T即可。注意权值的赋值。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 2147483646 #define ll long long #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) #define RI register ll #define up(p,i,n) for(ll i=p;i<=n;++i) #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=1100000; int n,m,len=1,S,T,maxflow,sum,t,h; int vis[MAXN],q[MAXN]; int lin[MAXN],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline int bfs() { memset(vis,0,sizeof(vis)); t=h=0;q[++t]=S;vis[S]=1; while(h++<t) { int x=q[h]; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(!e[i]||vis[tn])continue; vis[tn]=vis[x]+1; q[++t]=tn; if(tn==T)return 1; } } return 0; } inline int dinic(int x,int flow) { if(x==T)return flow; int rest=flow,k; for(int i=lin[x];i&&rest;i=nex[i]) { int tn=ver[i]; if(e[i]&&vis[tn]==vis[x]+1) { k=dinic(tn,min(e[i],rest)); if(!k)vis[tn]=0; e[i]-=k; e[i^1]+=k; rest-=k; } } return flow-rest; } int main() { //freopen("1.in","r",stdin); n=read();S=3002;T=S+1; for(int i=1;i<=n;++i) { int x=read();sum+=x; add(S,i,x); add(i,S,0); } for(int i=1;i<=n;++i) { int x=read();sum+=x; add(i,T,x); add(T,i,0); } m=read(); for(int i=1;i<=m;++i) { int x,y,z; x=read();y=read();z=read(); add(S,i+n,y);add(i+n,S,0); add(i+n+m,T,z);add(T,i+n+m,0); sum+=z+y; for(int j=1;j<=x;++j) { int k=read(); add(i+n,k,INF); add(k,i+n,0); add(k,i+n+m,INF); add(i+n+m,k,0); } } int flow=0; while(bfs())while((flow=dinic(S,INF)))maxflow+=flow; put(sum-maxflow); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号