树上斜率优化
斜率优化的时候有的时候可能会出在树上可是我并不会QWQ。

显然一个dp方程是 f[i]=min{f[j]+(d[i]-d[j])*p[i]+q[i]} 我们只需要取到最优决策j即可由于在树上这个复杂度还是n^2的。
考虑优化。 f[i]=f[j]+d[i]*p[i]-d[j]*p[i]+q[i]; f[j]=f[i]-d[i]*p[i]-q[i]+d[j]*p[i];
非常简单的优化然后考虑如何在树上进行 显然我们维护一个单调队列 然后每次到达一个点就修改 回溯的时候再回溯回来。
每次只有队尾一个元素修改改回来至于队首还原即可。显然这是暴力出队注意这里的pi是递增的!

//#include<bits/stdc++.h> #include<iostream> #include<queue> #include<iomanip> #include<cctype> #include<cstdio> #include<deque> #include<utility> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<cstdlib> #include<vector> #include<algorithm> #include<stack> #include<map> #include<set> #include<bitset> #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define INF 1000000000 #define ll long long #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=1000010; int n,l,r,len; ll f[MAXN],w[MAXN],now[MAXN]; ll d[MAXN],p[MAXN],q[MAXN]; int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1]; //f[i]表示第i个点到达根的最小花费 //f[i]=min(f[i],f[fa]+(d[i]-d[fa])*p[i]+q[i]); //f[i]=f[fa]+d[i]*p[i]-d[fa]*p[i]+q[i]; //f[i]=d[i]*p[i]+q[i]+f[fa]-d[fa]*p[i]; //f[fa]=f[i]-d[i]*p[i]-q[i]+d[fa]*p[i]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline double calculate(int x,int y) { return (f[y]-f[x])*1.0/(1.0*(d[y]-d[x])); } inline void dfs(int x,int father) { int nowl=l,nowr=r,tmp; while(l<r&&calculate(q[l],q[l+1])<=p[x])++l; f[x]=f[q[l]]+(d[x]-d[q[l]])*p[x]+w[x]; while(l<r&&calculate(q[r-1],q[r])>=calculate(q[r],x))--r; tmp=q[++r];q[r]=x; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; d[tn]=d[x]+e[i]; dfs(tn,x); } l=nowl;q[r]=tmp;r=nowr; return; } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=2;i<=n;++i) { int x,y; x=read();y=read(); add(x,i,y);add(i,x,y); p[i]=read();w[i]=read(); } l=1;r=0;dfs(1,0); for(int i=2;i<=n;++i)put(f[i]); return 0; }
显然这样出队是有风险的我们一条链后面跟一个菊花图就炸了复杂度仍是n^2的上界。
考虑出队的时候快速出队 发现是可以二分寻找位置直接出队的!

//#include<bits/stdc++.h> #include<iostream> #include<queue> #include<iomanip> #include<cctype> #include<cstdio> #include<deque> #include<utility> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<cstdlib> #include<vector> #include<algorithm> #include<stack> #include<map> #include<set> #include<bitset> #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define INF 1000000000 #define ll long long #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=1000010; int n,l,r,len; ll f[MAXN],w[MAXN],now[MAXN]; ll d[MAXN],p[MAXN],q[MAXN]; int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1]; //f[i]表示第i个点到达根的最小花费 //f[i]=min(f[i],f[fa]+(d[i]-d[fa])*p[i]+q[i]); //f[i]=f[fa]+d[i]*p[i]-d[fa]*p[i]+q[i]; //f[i]=d[i]*p[i]+q[i]+f[fa]-d[fa]*p[i]; //f[fa]=f[i]-d[i]*p[i]-q[i]+d[fa]*p[i]; inline void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline double calculate(int x,int y) { return (f[y]-f[x])*1.0/(1.0*(d[y]-d[x])); } inline void dfs(int x,int father) { int nowl=l,nowr=r,tmp; int L=l,R=r; while(L+1<R) { int mid=(L+R)>>1; if(calculate(q[mid],q[mid+1])<=p[x])L=mid; else R=mid; } if(calculate(q[L],q[R])<=p[x])l=R; else l=L; f[x]=f[q[l]]+(d[x]-d[q[l]])*p[x]+w[x]; L=l,R=r; while(L+1<R) { int mid=(L+R)>>1; if(calculate(q[mid-1],q[mid])>=calculate(q[mid],x))R=mid; else L=mid; } if(calculate(q[L],q[R])>=calculate(q[R],x))r=L; else r=R; tmp=q[++r];q[r]=x; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; d[tn]=d[x]+e[i]; dfs(tn,x); } l=nowl;q[r]=tmp;r=nowr; return; } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=2;i<=n;++i) { int x,y; x=read();y=read(); add(x,i,y);add(i,x,y); p[i]=read();w[i]=read(); } l=1;r=0;dfs(1,0); for(int i=2;i<=n;++i)put(f[i]); return 0; }
然鹅快不了多少2333


看起来和上一道题近乎一样却有很大的不同 1 斜率不再单调 (维护全凸包二分寻找决策)2 具有一个限制是 距离不得超过limit。
如果没有第二个限制的话其实跟上一道题是差不多的我们直接维护全凸包二分寻找决策即可。
但是有了距离的限制的话就有点麻烦了。。原因如下图:
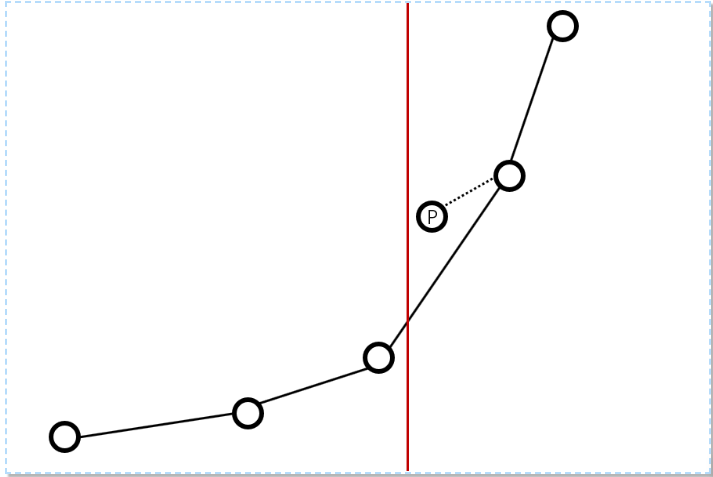
注意 p看起来是个上凸包是一定不优解 但是在限制之下 它有可能是最优的 没办法有限制比较难受。。
想了很久 发现看不懂线段树的做法 弃疗选择点分治吧。。(反正都是数据结构反正都学过)
点分治的话要考虑CDQ分治了 首先我们先考虑求出一个重心 然后发现重心到根的路径上的自己内部有答案贡献 且对外部对答案有贡献那么我们是可以先算里面的这样不断进行分治即可。
注意这里分治的话点分治复杂度 nlogn 然后递归的复杂度是logn的 套上一个排序 nlogn^2 然后O(n)便利+二分查找 时间复杂度仍然是nlog^2n 的。
非常巧妙注意此题是维护的是 右下方的凸包 巨坑我的二分一直挂 对拍才终于知道L&R 一直写反 我算是服了。

//#include<bits/stdc++.h> #include<iostream> #include<queue> #include<iomanip> #include<cctype> #include<cstdio> #include<deque> #include<utility> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<cstdlib> #include<vector> #include<algorithm> #include<stack> #include<map> #include<set> #include<bitset> #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) #define INF 1000000000 #define ll long long #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=200010; int n,T,r,len,root,top; int fa[MAXN],sz[MAXN],q[MAXN],vis[MAXN],s[MAXN]; ll p[MAXN],w[MAXN],f[MAXN],d[MAXN],lim[MAXN]; int lin[MAXN],nex[MAXN],ver[MAXN],rt[MAXN],st[MAXN]; inline int wy(int a,int b){return d[a]-lim[a]>d[b]-lim[b];} inline void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } inline void dis(int x) { for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; d[tn]+=d[x]; dis(tn); } return; } inline void getroot(int x,int sz) { rt[x]=1;s[x]=0; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn])continue; getroot(tn,sz); rt[x]+=rt[tn]; s[x]=max(s[x],rt[tn]); } s[x]=max(s[x],sz-rt[x]); if(s[x]<=s[root])root=x; return; } inline void dfs(int x) { st[++top]=x; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn])continue; dfs(tn); } return; } inline double calculate(int a,int b){return (f[b]-f[a])*1.0/(1.0*(d[b]-d[a]));} inline void insert(int x) { int L=1,R=r; if(L>R||L==R){q[++r]=x;return;} while(L+1<R) { int mid=(L+R)>>1; if(calculate(q[mid],q[mid-1])>=calculate(x,q[mid]))L=mid; else R=mid; } if(calculate(x,q[R])>=calculate(q[R],q[L]))r=L; else r=R; q[++r]=x; return; } inline int search(int x) { int L=1,R=r; if(L>R)return 0; if(L==R)return q[R]; while(L+1<R) { int mid=(L+R)>>1; if(calculate(q[mid],q[mid-1])<=x)R=mid; else L=mid; } if(calculate(q[R],q[L])<=x)return q[L]; return q[R]; } inline void CDQ(int x,int sz) { if(sz==1)return; int b,rt1;root=0;getroot(x,sz);rt1=root; for(int i=lin[rt1];i;i=nex[i]) { int tn=ver[i]; vis[tn]=1; sz-=rt[tn]; } CDQ(x,sz);top=0; for(int i=lin[rt1];i;i=nex[i])dfs(ver[i]); sort(st+1,st+1+top,wy); b=rt1;r=0; for(int i=1;i<=top;++i) { int tn=st[i]; while(b!=fa[x]&&d[b]>=d[tn]-lim[tn]) insert(b),b=fa[b];//注意此时队列之中d单调递减 if(r) { int j=search(p[tn]); f[tn]=min(f[tn],f[j]+(d[tn]-d[j])*p[tn]+w[tn]); } } for(int i=lin[rt1];i;i=nex[i])CDQ(ver[i],rt[ver[i]]); return; } int main() { //freopen("1.in","r",stdin); n=read();T=read(); for(int i=2;i<=n;++i) { fa[i]=read();d[i]=read(); add(fa[i],i); p[i]=read();w[i]=read();lim[i]=read(); } for(int i=2;i<=n;++i)f[i]=(ll)INF*(ll)INF; s[0]=INF; dis(1);CDQ(1,n); for(int i=2;i<=n;++i)put(f[i]); return 0; }
对拍:

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cstdio> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<algorithm> #include<queue> #include<deque> #include<vector> #include<map> #include<stack> #include<set> #include<bitset> #include<cstdlib> using namespace std; const int MAXN=110; int n,cnt,len; int lin[MAXN],ver[MAXN],nex[MAXN],d[MAXN],p[MAXN],q[MAXN]; int f[MAXN],ru[MAXN],fa1[MAXN]; int getfather(int x){return x==f[x]?x:getfather(f[x]);} inline void dfs(int x,int fa) { for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==fa)continue; dfs(tn,x); fa1[tn]=x; } } inline void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } int main() { freopen("1.in","w",stdout); //freopen("1.out","w",stdout); srand(time(0)); n=rand()%3+2;f[1]=1; cout<<n<<endl;cout<<1<<endl; for(int i=2;i<=n;++i)f[i]=i,p[i]=rand()%20+1,d[i]=rand()%20+1,q[i]=rand()%20+1; while(cnt<n-1) { int x=rand()%n+1; int y=rand()%n+1; int xx=getfather(x); int yy=getfather(y); if(xx==yy)continue; f[xx]=yy;++cnt; add(x,y);add(y,x); } dfs(1,0); for(int i=2;i<=n;++i) cout<<fa1[i]<<' '<<d[i]<<' '<<p[i]<<' '<<q[i]<<' '<<d[i]+rand()%20<<endl; return 0; }
造数据能力越来越强啦!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号