运输计划

　　原本是不打算写这道题的题解的看看自己的估值还是写吧。

其实是因为当年学长mzxnoip时考场上没有推出这道题今天我来推。（再忆学长当年风采）

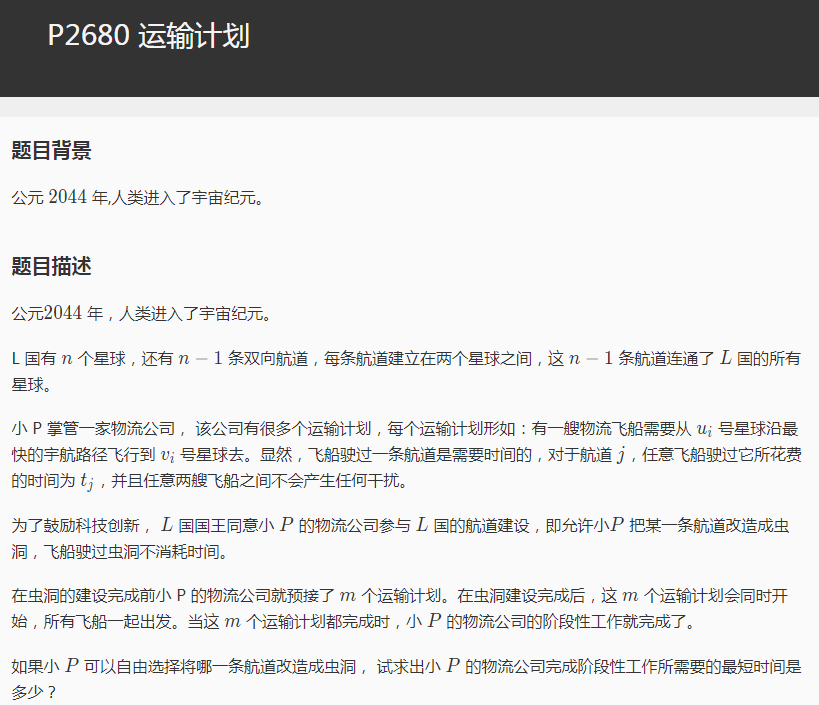
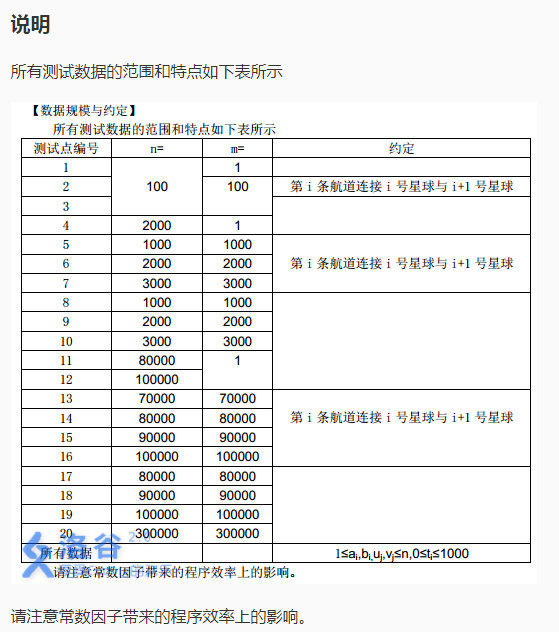
我来简化题意求m双点之间的距离 特殊的是可使图中的一条道路的边权为0求出所有距离的最大值使这个最大值尽量小。

最大的最小 二分我先记下看看有没有什么用。下面进入暴力时间：

仔细观察数据范围 m=1的时候显然 dfs一遍求出这条路径上的边权最大值 距离减去这个max边权即可。

期望得分20 （怪不得当年学长520） 

//#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<algorithm>
#include<vector>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<map>
#define INF 2147483646
#define ll long long
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define R register
#define up(p,i,n) for(int i=p;i<=n;++i)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<0?x=-x,putchar('-'):0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//运输计划 Author:Chdy
const int MAXN=300002;
int n,m,len,maxx,ans,st,en,flag;
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void dfs(int x,int father)
{
    if(x==en){flag=1;return;}
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father)continue;
        if(flag)return;
        dfs(tn,x);
        if(flag)maxx=max(maxx,e[i]),ans+=e[i];
    }
    return;
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    up(1,i,n-1)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    if(m==1)
    {
        st=read();en=read();
        dfs(st,en);
        put(ans-maxx);
    }
    return 0;
}

考虑再次暴力：暴力枚举每一条边要还是不要这样来计算最大值然后求出各个状态下的最大值

看上去似乎是n^3的但是有可能能过掉第10个点 加上第一个判断 期望得分60。

这个60分代码写起来比较费事 不如直接刚100.我想了一晚上加看了一眼某谷的讨论终于有解法了。

最大的最小 二分一个答案 。显然我们应该去掉的那一条边在最长的路径之上。

对于这些路径超过mid的路径 如果此mid是答案的话那么他们中一定有一条边是公共的去掉这条边即可使答案缩小这样来判定mid是否合法。

判定这条是公共的且是最长的边。这个怎么找如果我们再对这些边进行一个一个跑将会超时。

树上进行差分这个很不错每个点代表着它上面的那一条边 对整张图进行一次dfs便利即可。

大体思路就是这样。值得一提的是这样做事正确的显然。但是会被卡常修改一下而二分的上下界即可。

或者采用tarjan线性求出LCA也是可以的。卡常的上界为最长链 下界为最长链-max最长边（显然）

//#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<algorithm>
#include<vector>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<map>
#define INF 2147483646
#define ll long long
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define R register
#define up(p,i,n) for(int i=p;i<=n;++i)
#define x(i) t[i].x
#define y(i) t[i].y
#define lca(i) t[i].lca
#define z(i) t[i].z
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<0?x=-x,putchar('-'):0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//运输计划 Author:Chdy采用 LCA 二分 树上差分 
const int MAXN=300002;
int n,m,len,maxx,ans,flag,T,t1,h,sum,maxx1;
int q[MAXN],c[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
int depth[MAXN],vis[MAXN],dis[MAXN],f[MAXN][25];
struct wy
{
    int x,y;
    int lca;
    int z;
    friend int operator <(const wy a,const wy b)
    {
        return a.z>b.z;
    }
}t[MAXN];
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
inline void bfs()
{
    q[++t1]=1;
    while(h++<t1)
    {
        int te=q[h];vis[te]=1;
        for(int i=lin[te];i;i=nex[i])
        {
            int tn=ver[i];
            if(vis[tn])continue;
            maxx1=max(maxx1,e[i]);
            depth[tn]=depth[te]+1;
            dis[tn]=dis[te]+e[i];
            f[tn][0]=te;
            for(int j=1;j<=T;++j)f[tn][j]=f[f[tn][j-1]][j-1];
            q[++t1]=tn;
        }
    }
}
int LCA(int x,int y)
{
    if(depth[x]>depth[y])swap(x,y);
    for(int i=T;i>=0;--i)
        if(depth[f[y][i]]>=depth[x])y=f[y][i];
    if(x==y)return x;
    for(int i=T;i>=0;--i)
        if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
    return f[x][0];
}
inline void dfs(int x,int father)
{
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father)continue;
        dfs(tn,x);
        c[x]+=c[tn];
        if(c[tn]==sum)maxx=max(maxx,e[i]);
    }
}
inline int carcluate(int x)
{
    sum=0;maxx=0;
    memset(c,0,sizeof(c));
    if(z(1)<=x)return 1;
    for(int i=1;i<=n;++i)
    {
        if(z(i)<=x)break;
        ++c[x(i)];++c[y(i)];
        c[lca(i)]-=2;
        ++sum;
    }
    dfs(1,0);
    if(maxx==0)return 0;
    if(z(1)-maxx<=x)return 1;
    return 0;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    up(1,i,n-1)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    T=(int)(log(n*1.0)/log(2*1.0))+1;
    bfs();
    for(int i=1;i<=m;++i)
    {
        x(i)=read();y(i)=read();
        lca(i)=LCA(x(i),y(i));
        z(i)=dis[x(i)]+dis[y(i)]-(dis[lca(i)]<<1);
        maxx=max(maxx,z(i));
    }
    sort(t+1,t+1+m);
    //for(int i=1;i<=m;++i)cout<<z(i)<<endl;
    int l=maxx-maxx1,r=maxx;
    while(l+1<r)
    {
        int mid=(l+r)>>1;
        if(carcluate(mid))r=mid;
        else l=mid;
    }
    if(carcluate(l))put(l);
    else put(r);
    return 0;
}