数据结构优化dp
本以为自己的dp已经成熟了没想到在优化上面还是欠佳 或者是思路方面优化dp还不太行。

赤壁之战 当然 很有意思的题目描述 大体上是苦肉计吧 。盖黄 ...
题意是 求出长度为m的严格上升子序列的个数 这个还比较基础。阶段比较明显。
f[i][j] 表示前i个数字当中选出了j个数字的方案数 显然的状态转移是 f[i][j]+=f[k][j-1](a[k]<a[i]&&1<=k<i)
枚举状态 n^2 枚举决策 k O(n) 总复杂度 n^3 这样看起来是过不了这道题的。
考虑如∑快速寻找决策注意我们只要值不要k这个下标所以 线段树 树状数组搞一搞即可。
复杂度 n^2logn (注意将a[i]进行离散)没了。(注意循环顺序)

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define max(x,y) (x>y?x:y) #define min(x,y) (x>y?y:x) #define mod 1000000007 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=1002; int n,m,T,top,ans; int a[MAXN],b[MAXN],c[MAXN]; int f[MAXN][MAXN];//f[i][j] 表示前i个数字当中选出j个数字的方案数 //f[i][j]+=f[k][j-1](a[k]<a[i]) void discrete() { top=0; sort(a+1,a+1+n); for(int i=1;i<=n;++i)if(i==1||a[i]!=a[i-1])a[++top]=a[i]; for(int i=1;i<=n;++i)b[i]=lower_bound(a+1,a+1+top,b[i])-a; } void add(int x,int y) { for(;x<=top;x+=x&(-x))c[x]=(c[x]+y)%mod; return; } int ask(int x) { int cnt=0; for(;x;x-=x&(-x))cnt=(cnt+c[x])%mod; return cnt%mod; } int main() { //freopen("1.in","r",stdin); T=read(); for(int w=1;w<=T;++w) { memset(f,0,sizeof(f)); n=read();m=read();ans=0; for(int i=1;i<=n;++i)b[i]=a[i]=read(),f[i][1]=1; discrete(); for(int j=2;j<=m;++j) { memset(c,0,sizeof(c)); for(int i=1;i<=n;++i) { int xx=ask(b[i]-1); f[i][j]=(f[i][j]+xx)%mod; add(b[i],f[i][j-1]); } } for(int i=m;i<=n;++i)ans=(ans+f[i][m])%mod; printf("Case #%d: %d\n",w,ans); } return 0; }
算是很水的一道题目。
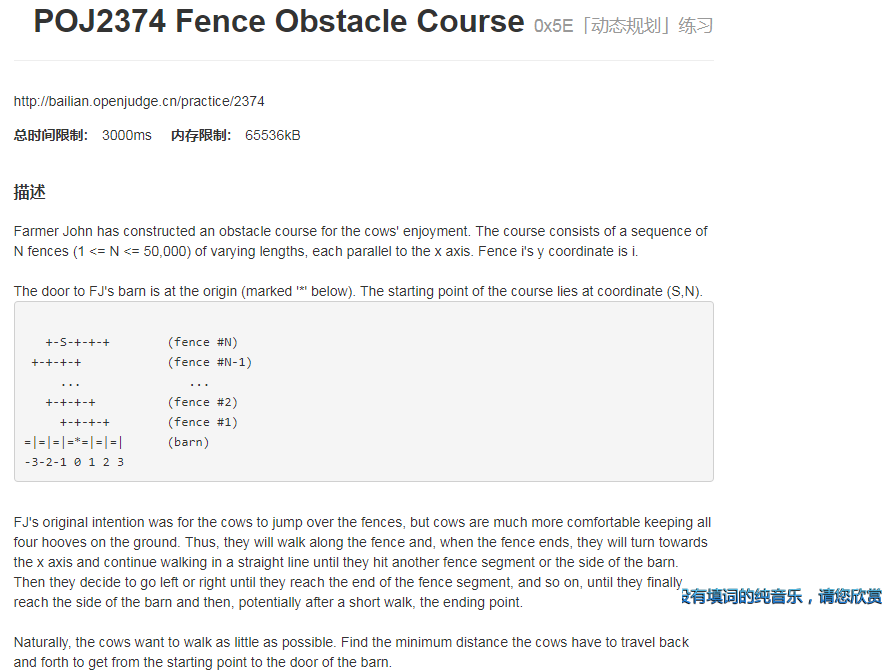
这道题是一个 什么东西 我首先想到一个O(n)的dp
f[i][0/1]表示到达第i个栅栏在其左端或者在其右端已经经过的最小距离。
显然 f[i][0]=min(f[i][0],min(f[i-1][1]+|y[i-1]-x[i]|,f[i-1][0]+|x[i]-x[i-1|);
或 f[i][1]=min(f[i][1],min(f[i-1][1]+|y[i-1]-y[i]|,f[i-1][0]+|y[i]-x[i-1|);
仔细观察貌似不太对 因为对于其他决策 1=<j<i 来说也是可以转移到i 的所以貌似这个不太对。
我继续想 有了 f[i][j] 表示到达第i个栅栏的第j个位置的最小价值
转移 f[i][j]=min(f[i][j],f[i-1][k]+|j-k|); 这个好,明显转移时正确的 因为是最优子结构嘛。
当然也显然 这个dp转移不太友好就算我将其坐标进行离散化 复杂度也是n^3的
显然 n^2的都不太能过别说n^3的了,我可以优化:
拆开绝对值 f[i][j]=min(f[i][j],f[i-1][k]+j-k);(k<=j) f[i][j]=min(f[i][j],f[i-1][k]+k-j) k>j
j为已知 不管 f[i-1][k]-k显然是具有单调性的单调队列优化寻找决策 里面存着最小的k这个决策即可。
对于k>j同理 神奇的发现这 优化到了n^2 非常有意思。
我好想能拿到绝大多数分了 但是这依然是在超时的边缘的。不管了我已经尽力了。
正解是这样的 对于第二个dp 这个状态是不优的 因为这样做毫无价值好吧。。。
存那么多点的状态其实没必要我们只需存对于某个栅栏的两个端点即可。
经过贪心我们可以发现 对于第一个dp 我们的状态转移时这样的 :
f[i][0]=min(f[k][0]+abs(x[i]-x[k]),f[k][1]+abs(w[k]-x[i]));
f[i][1]=min(f[k][0]+abs(x[k]-w[i]),f[k][1]+abs(w[k]-w[i]));
其中 1<=k<i (还有一些限制没写看起来状态转移是错的)
对于当前i这个栅栏我们要走到其两端那么我只用看是否有一个决策前面已经覆盖了这个端点如果覆盖了这个端点那么这个决策之前的所有决策都是不合法的 因为他们不能直接以直线的形式过来这有当前决策可以以直线过来,因为没有其他的栅栏挡住了它。
我们完全可以开个数组来模拟这个过程 仔细思考贪心是正确的。且不具后效性。
但是这有转移仍是n^2 考虑优化 对于线段覆盖区间这种问题应该是有一种做法叫做浮水法能以很快的时间做出。
类似于 HAoi某一年的贴海报 当然这道题我是直接线段树的。
那么这个区间覆盖直接线段树即可。值得一提的是有坑点。
起点和输入和终点是否连到一块需注意这个坑了我好久。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define l(x) t[x].l #define r(x) t[x].r #define add(x) t[x].add #define k(x) t[x].k #define z p<<1 #define y p<<1|1 #define max(x,y) (x>y?x:y) #define min(x,y) (x>y?y:x) using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50002,maxn=100001; int n,m; int x[MAXN],w[MAXN]; ll f[MAXN][2];//f[i][0/1]表示到达第i个栅栏的左边或者右边值最优 struct wy { int l,r; int k;//决策 int add; }t[(maxn<<3)+2]; void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r)return; int mid=(l+r)>>1; build(z,l,mid); build(y,mid+1,r); return; } void pushdown(int p) { add(y)=add(z)=add(p); k(y)=k(z)=add(p); add(p)=0;return; } void change(int p,int l,int r,int v) { if(l<=l(p)&&r>=r(p)) { add(p)=v; k(p)=v; return; } if(add(p))pushdown(p); int mid=(l(p)+r(p))>>1; if(l<=mid)change(z,l,r,v); if(r>mid)change(y,l,r,v); return; } int ask(int p,int e) { if(l(p)==r(p))return k(p); int mid=(l(p)+r(p))>>1; if(add(p))pushdown(p); if(e<=mid)return ask(z,e); else return ask(y,e); } int main() { //freopen("1.in","r",stdin); n=read();m=read(); memset(f,10,sizeof(f)); for(int i=1;i<=n;++i) { x[i]=read()+maxn; w[i]=read()+maxn; } build(1,1,maxn<<1); f[0][0]=f[0][1]=0; x[0]=maxn;w[0]=maxn; for(int i=1;i<=n;++i) { int k1=ask(1,x[i]); int k2=ask(1,w[i]); f[i][0]=min(f[k1][0]+abs(x[i]-x[k1]),f[k1][1]+abs(w[k1]-x[i])); f[i][1]=min(f[k2][0]+abs(x[k2]-w[i]),f[k2][1]+abs(w[k2]-w[i])); change(1,x[i],w[i],i); } put(min(f[n][1]+abs(w[n]-m-maxn),f[n][0]+abs(x[n]-m-maxn))); return 0; }
dp很有意思



 浙公网安备 33010602011771号
浙公网安备 33010602011771号