点分治

 点分治是个好东西 学长说今年省选day2 T3 有40分可以是点分治 有点难受如果我当初学了点分治该有多好啊。

所谓点分治就是在树上搞一些分治操作让复杂度大大降低。

这道题询问树上是否有任意两点之间的距离为k 考虑暴力 m指询问数 

暴力枚举 加dfs跑距离 所以复杂度是mn^3 期望得分 30

由于是一棵无根树所以考虑以1位根节点提前预处理出树上任意点距根的距离。

然后 暴力枚举两个端点 求出LCA 然后 d[x]+d[y]-(d[LCA]<<1)判断即可。

复杂度 mn^2logn期望得分60 很不错了~

正解释点分治：其实点分治是一种另类的分治方法基于树上的分治。

先处理过根的边 然后分治处理根的子树这样递归处理 考虑每次选根都是树的重心处。

所以总递归层数为logn 在每一层中暴力判断和过根的边的联系的边然后进行判断复杂度O(n)

总复杂度mnlogn 期望得分：100；这样巧妙的利用了分治思想和不断的选择重心 使复杂度骤降。

因为一些小细节打挂了所以浪费了点时间来检查。

首先是对于树的重心的处理 然后是分治点 然后在每个点中进行答案的统计即可。

复杂度mnlogn 可以AC。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define ll long long
#define max(x,y) (x>y?x:y)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//点分治 Author:chdy
const int MAXN=10002,maxn=10000002;
int n,m,k,len,sum,t,h;//sum 当前递归到的这颗子树大小
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
int vis[MAXN],f[MAXN];//f[i]表示以i为根时的最大子树大小
int sz[MAXN],query[MAXN];//表示以i为根时其子树的节点个数
int ans[MAXN],q[MAXN],dis[MAXN],tmp[MAXN];
bool judge[maxn];
int root;
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
inline void getroot(int x,int fa)
{
    f[x]=0;sz[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==fa||vis[tn])continue;//注意两个条件
        getroot(tn,x);
        sz[x]+=sz[tn];
        f[x]=max(f[x],sz[tn]);
    }
    f[x]=max(f[x],sum-sz[x]);
    if(f[x]<f[root]||root==0)root=x;
    return;
}
inline void getdis(int x,int father)
{
    tmp[++h]=dis[x];
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;//注意两个条件
        dis[tn]=dis[x]+e[i];
        getdis(tn,x);
    }
}
void carcluate(int x)
{
    t=0;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        dis[tn]=e[i];h=0;
        getdis(tn,x);
        for(int j=1;j<=m;++j)
            for(int k=1;k<=h;++k)
            if(query[j]>=tmp[k])ans[j]|=judge[query[j]-tmp[k]];
        for(int j=1;j<=h;++j)q[++t]=tmp[j],judge[tmp[j]]=1;
    }
    for(int i=1;i<=t;++i)judge[q[i]]=0;
    return;
}
inline void sol(int x)
{
    vis[x]=1;judge[0]=1;
    carcluate(x);
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        sum=sz[tn];root=0;
        getroot(tn,x);
        if(sz[tn]==1)continue;
        sol(root);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<n;++i)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    for(int i=1;i<=m;++i)query[i]=read();
    sum=n;root=0;
    getroot(1,0);sol(root);
    for(int i=1;i<=m;++i)ans[i]?puts("AYE"):puts("NAY");
    return 0;
}

这道题是一个裸的点分治 我也就码了1h 然而错误百出可能是心不在焉吧。

什么数组开大 什么边都存错 什么重心找错 什么变量名打错 什么求出重心后没有使用。我弃疗了。

但是 坚持检查了20min 在爆零两次的基础之下 艰难的AC了（我是真的菜）

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define ll long long
#define mod 3
#define max(x,y) (x>y?x:y)
#define min(x,y) (x>y?y:x)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//点分治 Author:chdy
const int MAXN=20002;
int n,sum,s1,s2,t,h,root,g,len;
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
int sz[MAXN],f[MAXN],judge[4],q[MAXN],dis[MAXN],vis[MAXN];
int gcd(int a,int b){return b?gcd(b,a%b):a;}
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void getroot(int x,int father)
{
    sz[x]=1;f[x]=0;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        getroot(tn,x);
        sz[x]+=sz[tn];
        f[x]=max(f[x],sz[tn]);
    }
    f[x]=max(f[x],sum-sz[x]);
    if(f[x]<f[root]||root==0)root=x;
    return;
}
void getdis(int x,int father)
{
    q[++t]=dis[x];
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        dis[tn]=dis[x]+e[i];
        getdis(tn,x);
    }
    return;
}
void carcluate(int x)
{
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        t=0;dis[tn]=e[i];
        getdis(tn,x);
        for(int j=1;j<=t;++j)s1+=judge[(mod-q[j]%mod)%mod];
        for(int j=1;j<=t;++j)++judge[q[j]%mod];
    }
    judge[1]=0;judge[2]=0;
    return;
}
void sol(int x)
{
    vis[x]=1;judge[0]=1;
    carcluate(x);
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        if(sz[tn]==1)continue;
        root=0;sum=sz[tn];
        getroot(tn,x);
        sol(root);
    }
    return;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    for(int i=1;i<n;++i)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    sum=n;s2=n*n;getroot(1,0);
    sol(root);s1=s1*2+n;
    g=gcd(s2,s1);
    printf("%d/%d\n",s1/g,s2/g);
    return 0;
}

其实这道题应该是树形dp 在我A掉后看题解发现树形dp非常简单而且貌似复杂度还是线性的。

上面好像没有提到点分治的复杂度 的计算首先 为了保证不是n^2的点分治

我们必须求重心 求出来重心之后 最多被分出n/2大小的子树再对这颗子树进行分治最大子树为n/4

这样一棵树被我们递归了logn层 然后求重心是O(n)的 再加上分治时的计算也是O(n)的

总复杂度 nlogn.非常巧妙 的算法 。

下面是dp写法：设f[x][j]表示以x为根节点为j的数量。

然后考虑状态转移和答案的统计 具体细节还是很好想的。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define ll long long
#define mod 3
#define max(x,y) (x>y?x:y)
#define min(x,y) (x>y?y:x)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//树形dp Author:chdy
const int MAXN=20002;
int n,s2,g,len,ans;
int vis[MAXN];
int f[MAXN][3];//f[i][j]表示在i这颗子树当中j的数量
//显然的状态转移是 f[tn][j]->f[x][(j+e[i])%mod]
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
int gcd(int a,int b){return b?gcd(b,a%b):a;}
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void dp(int x)
{
    vis[x]=1;f[x][0]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        dp(tn);
        for(int j=0;j<=2;++j)ans+=f[tn][j]*(f[x][(mod-(j+e[i])%mod)%mod]);
        for(int j=0;j<=2;++j)f[x][(j+e[i])%mod]+=f[tn][j];
    }
    return;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    for(int i=1;i<n;++i)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    dp(1);s2=n*n;
    ans=(ans<<1)+n;g=gcd(s2,ans);
    printf("%d/%d\n",ans/g,s2/g);
    return 0;
}

还有一道例题：

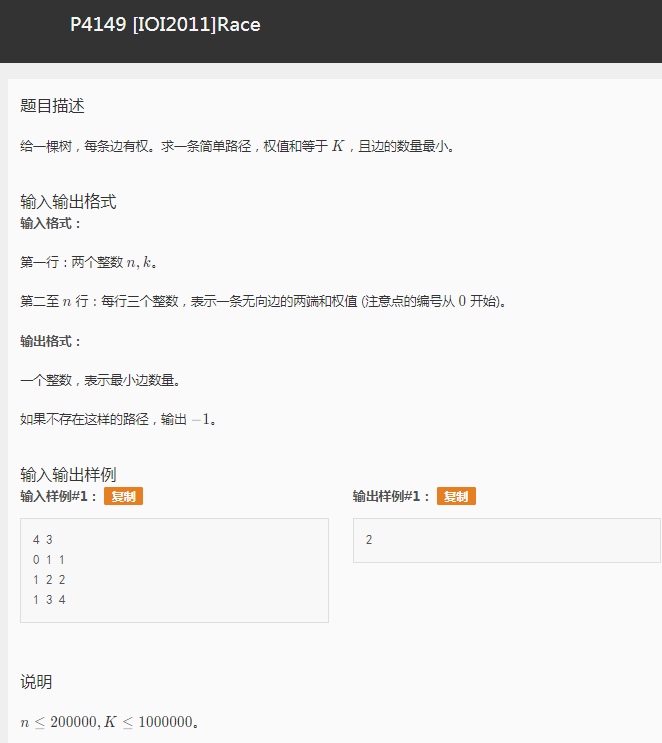
求 一条长度为k的路径且边数最小 一眼 树形dp吧 然后发现 

f[n][k]早就爆掉了空间我们不能这样dp 那么暴力一点点分治 吧 复杂度先算好 没有extra操作那么复杂度为nlogn

感觉和第一题差不多只不过是求最少边数 想象一下 我能否维护这个性质

应该是可以的吧 在统计时判断一下即可 至于如何统计路径数貌似只需在第一题的基础上加一些小判断吧。

然后被打脸了 没有缜密的思维 如何快速A题呢 我觉得我还没有养成能把所有细节都注意的到的人。

调了将近4h 才调过细节让我几近崩溃。。。

原因：我根本没有考虑到当边权超过k后我如何处理 。第一次我是这样处理的：不作为

导致RE+wa 非常不爽45分 。 RE？我把数组开大 开大十倍 80分接近正确。

然后想到如果有边权是大于k的呢是不是彻底没用啊。

第二次我是这样处理的：if(z>maxn-20)continue; 

这样的做法绝对是错误的，因为失去一条边意味着整张图都不再连通了 我在连通块中又没做点分治。

然后还是wa 看看题解 发现跟题解上处理方法不一样 然后改成题解的方法（我改的是个假的）

第三次我是这样处理的：

void getdis(int x,int father)
{
    q[++t]=dis[x];
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        if(dis[x]+e[i]>k)return;
        dis[tn]=dis[x]+e[i];
        getdis(tn,x);
    }
    return;
}

这个return 看似和题解上的差不多 其实差远了。

其中再次记录我wa掉一个点的原因 ：问号表达式写挂了 95分 问号表达式改成if语句就过了 可能是我的问号表达式写的太玄学了。

不能这样因为可能旁边的边还是合法的我这个一不合法就直接return 必定得到错误答案。

应该是dfs 型来getdis才对这样可以使很多信息得到。

inline void getdis(int x,int father,int d1,int d2)
{
    if(d1>k)return;
    tmp[++h]=x;dis[x]=d1;w[x]=d2;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        getdis(tn,x,d1+e[i],d2+1);
    }
}

当然这样做也是可以的：

inline void getdis(int x,int father)
{
    tmp[++h]=x;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        if(dis[x]+e[i]>k)continue;
        dis[tn]=dis[x]+e[i];
        w[tn]=w[x]+1;
        getdis(tn,x);
    }
}

思维一定要缜密 代码一定要简洁。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define ll long long
#define judge(i) s[i].judge
#define b(i) s[i].b
#define max(x,y) (x>y?x:y)
#define min(x,y) (x>y?y:x)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//点分治 Author:chdy
const int MAXN=200020,maxn=1000020;
int n,k,maxx=MAXN,len,sum,t,h,root;//sum 当前递归到的这颗子树大小
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
int vis[MAXN],f[MAXN];//f[i]表示以i为根时的最大子树大小
int sz[MAXN];//表示以i为根时其子树的节点个数
int q[MAXN],dis[MAXN],tmp[MAXN],w[MAXN];
struct wy{int b;bool judge;}s[maxn];
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void getroot(int x,int father)
{
    sz[x]=1;f[x]=0;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        getroot(tn,x);
        sz[x]+=sz[tn];
        f[x]=max(f[x],sz[tn]);
    }
    f[x]=max(f[x],sum-sz[x]);
    if(f[x]<f[root]||root==0)root=x;
    return;
}
inline void getdis(int x,int father,int d1,int d2)
{
    if(d1>k)return;
    tmp[++h]=x;dis[x]=d1;w[x]=d2;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father|vis[tn])continue;
        getdis(tn,x,d1+e[i],d2+1);
    }
}
void carcluate(int x)
{
    t=0;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        getdis(tn,x,e[i],1);
        for(int j=1;j<=h;++j)
            if(k-dis[tmp[j]]>=0)
                if(judge(k-dis[tmp[j]]))
                    maxx=min(maxx,b(k-dis[tmp[j]])+w[tmp[j]]);
        for(int j=1;j<=h;++j)
        {
            q[++t]=tmp[j];
            if(judge(dis[tmp[j]]))b(dis[tmp[j]])=min(b(dis[tmp[j]]),w[tmp[j]]);
            else judge(dis[tmp[j]])=1,b(dis[tmp[j]])=w[tmp[j]];
        }
    }
    for(int i=1;i<=t;++i)judge(dis[q[i]])=0;
    return;
}
inline void sol(int x)
{
    vis[x]=1;b(0)=0;judge(0)=1;
    carcluate(x);
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        if(sz[tn]==1)continue;
        sum=sz[tn];root=0;
        getroot(tn,x);
        sol(root);
    }
}
int main()
{
    freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    n=read();k=read();
    for(int i=1;i<n;++i)
    {
        int x,y,z;
        x=read()+1;y=read()+1;z=read();
        add(x,y,z);add(y,x,z);
    }
    if(k==0){put(0);return 0;}
    sum=n;getroot(1,0);
    sol(root);
    maxx==MAXN?put(-1):put(maxx);
    return 0;
}

update：发现书上的例题没写就溜了下午写了2h 一A了还不错 。

简单的树上维护一些东西 getdis时在树状数组中统计答案即可 复杂度 nlog^2n k不是很大跑的很快

//#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<algorithm>
#include<vector>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<map>
#define INF 2147483646
#define ll long long
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define R register
#define up(p,i,n) for(int i=p;i<=n;++i)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?x=-x,putchar('-'):0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//点分治 Author:Chdy
const int MAXN=40002,maxn=20002;
int n,len,k,sum,root,t,ans,h;
int q[MAXN],sz[MAXN],f[MAXN],vis[MAXN],c[MAXN],tmp[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
inline void add1(int x,int y)
{
    for(;x<=maxn;x+=x&(-x))c[x]+=y;
    return;
}
inline int ask(int x)
{
    int cnt=0;
    for(;x;x-=x&(-x))cnt+=c[x];
    return cnt;
}
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
inline void getroot(int x,int father)
{
    f[x]=0;sz[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]||tn==father)continue;
        getroot(tn,x);
        sz[x]+=sz[tn];
        f[x]=max(f[x],sz[tn]);
    }
    f[x]=max(f[x],sum-sz[x]);
    if(f[x]<f[root]||root==0)root=x;
    return;
}
inline void getdis(int x,int father,int dis)
{
    if(dis>k)return;
    tmp[++h]=dis;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        getdis(tn,x,dis+e[i]);
    }
    return;
}
inline void carcluate(int x)
{
    t=0;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        h=0;getdis(tn,x,e[i]);
        for(int j=1;j<=h;++j)if(k-tmp[j]!=0)ans+=ask(k-tmp[j]);
        for(int j=1;j<=h;++j)q[++t]=tmp[j],add1(tmp[j],1);
    }
    for(int i=1;i<=t;++i)
    {
        if(q[i]<=k)++ans;
        add1(q[i],-1);
    }
    return;
}
inline void sol(int x)
{
    vis[x]=1;carcluate(x);
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        if(sz[tn]==1)continue;
        sum=sz[tn];
        root=0;getroot(tn,x);
        sol(root);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    up(1,i,n-1)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    k=read();
    sum=n;getroot(1,0);
    //put(root);
    sol(root);
    put(ans);
    return 0;
}

题解中 是双指针 （我原来写的双指针觉得不太对环树状数组了）

直接暴力排序 然后双指针进行扫描 然后 一定有不合法的情况容斥一下即可。

//#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<algorithm>
#include<vector>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<map>
#define INF 2147483646
#define ll long long
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define R register
#define up(p,i,n) for(int i=p;i<=n;++i)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?x=-x,putchar('-'):0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//点分治 Author:Chdy
const int MAXN=40002,maxn=20002;
int n,len,k,sum,root,t,ans,h;
int q[MAXN],sz[MAXN],f[MAXN],vis[MAXN],c[MAXN],tmp[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
inline void add1(int x,int y)
{
    for(;x<=maxn;x+=x&(-x))c[x]+=y;
    return;
}
inline int ask(int x)
{
    int cnt=0;
    for(;x;x-=x&(-x))cnt+=c[x];
    return cnt;
}
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
inline void getroot(int x,int father)
{
    f[x]=0;sz[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]||tn==father)continue;
        getroot(tn,x);
        sz[x]+=sz[tn];
        f[x]=max(f[x],sz[tn]);
    }
    f[x]=max(f[x],sum-sz[x]);
    if(f[x]<f[root]||root==0)root=x;
    return;
}
inline void getdis(int x,int father,int dis)
{
    if(dis>k)return;
    q[++t]=dis;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(tn==father||vis[tn])continue;
        getdis(tn,x,dis+e[i]);
    }
    return;
}
inline int carcluate(int x,int d)
{
    int cnt=0;t=0;q[++t]=d;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        getdis(tn,x,e[i]+d);
    }
    sort(q+1,q+1+t);
    int l=1,r=t;
    while(l<r)
    {
        if(q[l]+q[r]<=k)cnt+=r-l,++l;
        else --r;
    }
    return cnt;
}
inline void sol(int x)
{
    vis[x]=1;ans+=carcluate(x,0);
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn])continue;
        if(sz[tn]==1)continue;
        ans-=carcluate(tn,e[i]);
        sum=sz[tn];
        root=0;getroot(tn,x);
        sol(root);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    up(1,i,n-1)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }
    k=read();
    sum=n;getroot(1,0);
    //put(root);
    sol(root);
    put(ans);
    return 0;
}