一双木棋

　　

去年省选题 第一题 也是最简单的一道题却也并不简单。

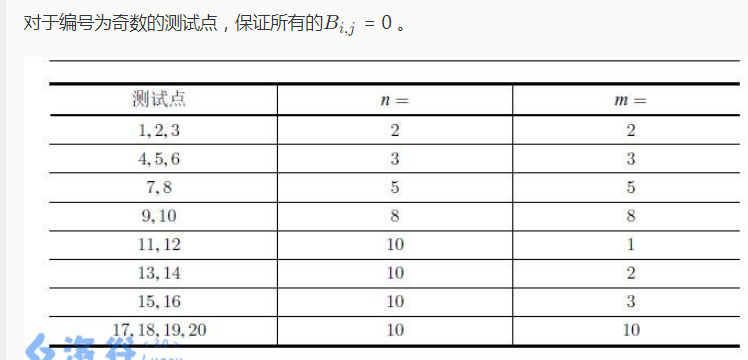
无疑 暴力是一定要打的 但是 300分纯暴力我也只能搞70分 不能上200分 是进不了省队的 （所以我凉透了）

今年 看吧 能A掉第一题 那么希望就很大 看暴力得分。

做题历程：轮流交替放放的位置每次都要枚举啊，且还有不合法的状态 n m只有10  考虑 状压啊 可是 这是100 2^100 这个肯定压不了

那肯定就是一个 dp 设状态吧 设 f[i][j] 表示 第i j 个格子拿了之后所能得到的最大价值 貌似转移都具有 后效性 且这个 还不好转移。

因为阶段不够明显 弃疗 暴力 搜索吧 我乱搜还不行么 抱歉不行。

这是一个对抗搜索 至于双方都要取最优 那么 这时需要 设一个状态什么的 。。。

我是连对抗搜索的不知道的NC 所以直接 阶乘级别的搜索 且 不算是搜索 因为25分根本不需要搜就可以特判得到。。

搜索的话阶乘级别搜索 对方下 - b[x][y] 自己下取min  +a[x][y]取max 即可 。

这样的话 就有40分了 很不错了。。。 代码也比较好写 这种方法叫做 对抗搜索。

考虑状压 因为我们搜索 的状态好多都不必要且重复所以 记忆化搜索也应该上场了 想要记忆化我们必须得对下一个局面 的整个局面都要取得最优解且 这样记忆化就可以了。至于状态 必须 要设计一个包容整个状态空间的且 不具 后效性的才行。

网上大多题解千篇一律 都是 轮廓线dp 我认为 这个的确是非常必要的 因为 对整个棋盘进行状压的话是不可能的。

对轮廓进行状压 这样还能保证 状态后效性 且这里注意 设计这个状态的 意义：

1 对于任一一个状态 面对这样局势的只会是一个人而并非两人任意 也就是说 不会出现一种局面两个人都可能遇到。

2 这个状态是无后效性的 想想都知道了 局部最优且不影响全局 进而推得最优解。

3 状态的表示 转移 都比较好操作所以极力推荐 ！！！

把竖着的线当做 1 横着当做0 第一个状态有了 111...000... 目标状态 也有了 000...111...

但是 出发由谁出发呢？假设从初状态 开始 ，转移没问题可是后效性呢？如果那样想我每伸入一层 

都要对当前这层进行最优值的 转移 等到当前这层取完了最优解了我再回溯上一层后效性得到了保证 没问题！

貌似从初状态出发还记搜什么直接顺着向下推不就好了么 ？很奇怪的问题！！！写记忆化还从没遇到过这种情况

这里明确一下 ： 记忆化搜索知道已知状态 由未知状态去 搜索 然后没了我从已知状态开始搜索了 很不对头。。。

正着 的确是有问题的下面是问题代码：

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define INF 2147483646
#define ll long long
#define db double
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[70];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const int MAXN=12;
int n,m;
int a[MAXN][MAXN],b[MAXN][MAXN];
int f[1<<20],vis[1<<20];
int q[1<<20],p[1<<20],t,h;
//设f[i]表示在i这个轮廓线上所能得到的最大差值。
inline int min(int x,int y){return x>y?y:x;}
inline int max(int x,int y){return x>y?x:y;}
void bfs()
{
    q[++t]=(((1<<n)-1)<<m);
    p[t]=1;vis[q[t]]=1;//f[q[t]]=0;
    while(h++<t)
    {
        int state=q[h];
        if(state==(1<<n)-1)return;
        int x=n+1,y=1;
        for(int i=n+m-1;i>0;--i)
        {
            if(state>>i&1)--x;
            else ++y;
            if((state&(3<<(i-1)))!=(1<<i))continue;
            int now=state^(3<<(i-1));
            if(p[h]&&(!vis[now]))f[now]=INF;
            if((!p[h])&&(!vis[now]))f[now]=-INF;
            if(p[h])f[now]=min(f[now],f[state]+a[x][y]);
            else f[now]=max(f[now],f[state]-b[x][y]);
            if(!vis[now]){vis[now]=1;q[++t]=now,p[t]=p[h]^1;}
        }
    }
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)a[i][j]=read();
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)b[i][j]=read();
    bfs();
    put(f[(1<<n)-1]);
    return 0;
}

发现具有后效性 按照我的话来说就是每一步状态都和上一层紧密相连 且是动点动状态 非常不友好的后效性。

于是乎 因为如果正着推，有可能出现当前虽然求出了最大价值，但是却不是他们的最优策略的情况最优策略这个东西 正着推是不对滴！！！

因为不知道取哪个上一步的才是最优策略状态。上一层状态对我们当前这层状态真的有深深的影响我不想了。总之不能dp

考虑倒序 选择当前点 我只在乎形成这个轮廓的对于形成这个轮廓的最优决策即可。好像没有后效性诶。

只要每个地方做好 当前的状态只和当前定点有关 直接承接上一步的最优决策下的最优状态即可。

可是 最后是谁选呢 比较麻烦 我们做一个这样的处理 状态是倒着 可是我们正着拿格子 

也就是最后一个状态对应第一个格子 因为第一个格子是有主的 。好了没问题了维护完毕！

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define INF 2147483646
#define ll long long
#define db double
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[70];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
//考虑轮廓线dp 状态可推到下一个状态所以 我认为当前状态如果最优
//推到下一个状态也可以是最优的 所以我认为是无后效性的
//竖行表示1 横行表示0 状态总数 (1<<(n+m))-1
//正着向后不断推 倒着搜索
const int MAXN=12;
int n,m;
int a[MAXN][MAXN],b[MAXN][MAXN];
int f[1<<20],vis[1<<20];
//设f[i]表示在i这个轮廓线上所能得到的最大差值。
inline int min(int x,int y){return x>y?y:x;}
inline int max(int x,int y){return x>y?x:y;}
int dfs(int state,int p)
{
    if(vis[state])return f[state];
    int x=n+1,y=1;
    if(p)f[state]=-INF;
    else f[state]=INF;
    for(int i=0;i<n+m-1;++i)
    {
        if(state>>i&1)x--;else ++y;
        if((state>>i&3)!=1)continue;
        int now=state^(3<<i);
        if(p)f[state]=max(f[state],dfs(now,p^1)+a[x][y]);
        else f[state]=min(f[state],dfs(now,p^1)-b[x][y]);
    }
    vis[state]=1;
    return f[state];
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)a[i][j]=read();
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)b[i][j]=read();
    vis[((1<<n)-1)<<m]=1;
    dfs((1<<n)-1,1);
    put(f[(1<<n)-1]);
    return 0;
}

去年春恨却来时。落花人独立，微雨燕双飞。