矩阵乘法高级操作
对于矩阵乘法的一些操作 我们 其实 大部分是 多追加一个系数 或者和 其他算法连在一起。
至于核心无非就是 先列出dp 方程再优化 或者 直接 对题目进行建模 构建矩阵。
至于矩阵乘法的正确性 形状的正确性 是可以证明的 但是内部最真实的正确性我还无法证明。
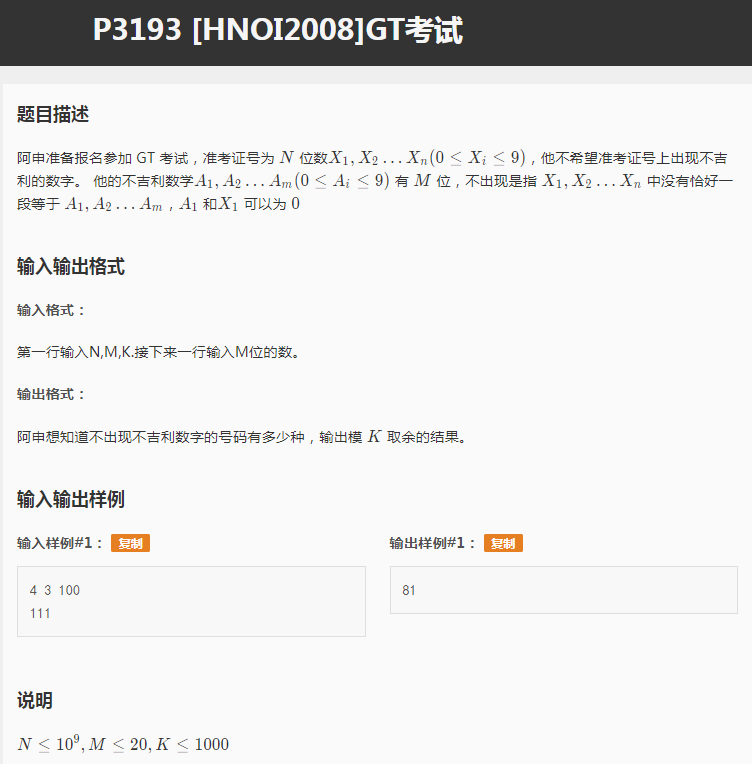
这道题是 字符串类型的题目 求方案数 很烦 大部分都是和KMP算法是连在一起的因为对于不存在当前的子串个个数,就只能KMP的方法寻求方案数了。
设 f[i][j] 表示第一个字符串 匹配到了第i个第二个字符匹配到第j个字符的且不重复的方案数。
那么此时有状态转移 f[i][j]+=f[i-1][k]+g[k][j] 由于这个是字符串的匹配 借助KMP算法 我们是可以求得g数组的。
然后 有了状态转移我们可以 很轻易的 构建出矩阵 f[i]表示第i个字符加上后 已经匹配第二个字符串的到第j位方案数 只要没有匹配到 m位那么这些状态都是合法的。
乘上状态矩阵 g即可。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define INF 2147483646 #define ll long long #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=26; int n,m,ans; int mod; char ch[MAXN]; int a[MAXN],f[MAXN];//f[i]表示第n个数字的第i位所和j匹配的位的方案数 int g[MAXN][MAXN];//g[i][j] 表示匹配前i的串转到匹配前j的串的方案数。 int nex[MAXN]; void KMP() { nex[1]=0; int j=0; for(int i=2;i<=m;++i) { while(j&&a[j+1]!=a[i])j=nex[j]; if(a[j+1]==a[i])++j; nex[i]=j; } for(int i=0;i<m;++i) for(int k=0;k<=9;++k) { j=i; while(j&&a[j+1]!=k)j=nex[j]; if(a[j+1]==k)++j; if(j<m)++g[i][j]; } return; } struct wy { int f[MAXN]; int b[MAXN][MAXN]; wy(){memset(f,0,sizeof(f));memset(b,0,sizeof(b));} friend wy operator *(wy a,wy b) { wy tmp; for(int i=0;i<m;++i) for(int j=0;j<m;++j) for(int k=0;k<m;++k) tmp.b[i][j]=(tmp.b[i][j]+(a.b[i][k]*b.b[k][j])%mod)%mod; return tmp; } friend wy operator -(wy a,wy b) { wy tmp; for(int i=0;i<m;++i) for(int j=0;j<m;++j) tmp.f[i]=(tmp.f[i]+(a.f[j]*b.b[j][i])%mod)%mod; return tmp; } friend wy operator ^(wy a,int p) { wy tmp;tmp.f[0]=1; while(p) { if(p&1)tmp=tmp-a; p=p>>1; a=a*a; } return tmp; } }A; int main() { //freopen("1.in","r",stdin); n=read();m=read();mod=read(); scanf("%s",ch+1); for(int i=1;i<=m;++i)a[i]=ch[i]-'0'; KMP(); for(int i=0;i<m;++i) for(int j=0;j<m;++j)A.b[i][j]=g[i][j]; A=A^n; for(int i=0;i<m;++i)ans=(ans+A.f[i])%mod; put(ans%mod); return 0; }
代码比从前规范很多 结构体重载运算符的话不容易出错。
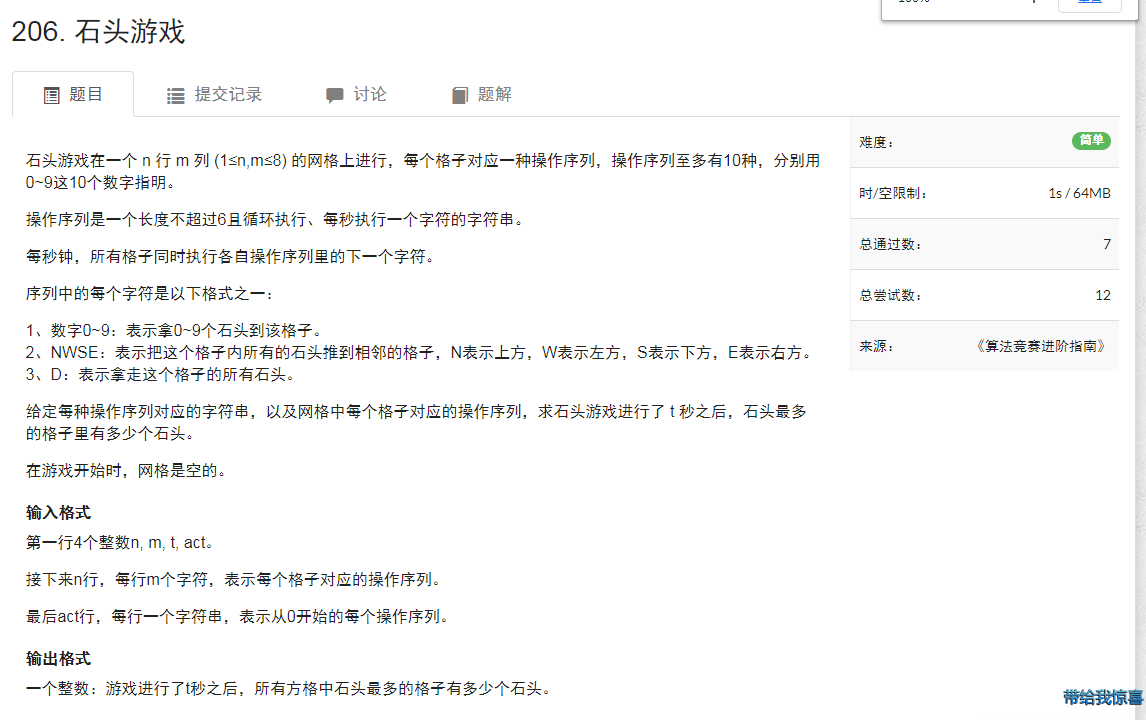
这道题不知道为什么竟然是简单 我很难受的码了 2h 然后调了1h 然后才一步步AC 真的是不容易。(为什么是简单啊 我太菜了)
细节颇多 直接考虑构建矩阵 发现每个格子操作不同步 好像只能单步乘 那这 考虑LCM 发现是60
然后乘完以后剩下的rest<60 单步乘即可。
对于一个格子放上石头 那么此时 我们需要一个格子来给他石头多开一个系数格子给他吧。
对于答案我们只需每个格子中有多少个格子数而二维矩阵无疑没什么用考虑压维。
压维的原因也可以这样考:对于这个一维矩阵我们轻而易举的就构建出来一个二维的矩阵而对于一个二维矩阵我们无法构建出四维矩阵啊。。
然后状态的话很繁杂具体细节看code.

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define INF 2147483646 #define ll long long #define db double #define x(i) t[i].x #define y(i) t[i].y #define z(i) t[i].z using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; ll num=0;char ch[70]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const ll MAXN=70; ll n,m,N,maxx; ll T,act,nece,rest;//necessary char ch[MAXN][MAXN],c[MAXN][MAXN]; ll pos[MAXN][MAXN],flag[MAXN]; ll a[MAXN][MAXN][MAXN]; struct wy { ll f[MAXN];//答案矩阵 ll b[MAXN][MAXN];//状态矩阵 wy(){memset(b,0,sizeof(b));memset(f,0,sizeof(f));} friend wy operator *(wy a,wy b) { wy tmp; for(ll i=0;i<=N;++i) for(ll j=0;j<=N;++j) for(ll k=0;k<=N;++k)tmp.b[i][j]+=a.b[i][k]*b.b[k][j]; return tmp; } friend wy operator -(wy a,wy b) { wy tmp; for(ll i=0;i<=N;++i) for(ll j=0;j<=N;++j)tmp.f[i]+=a.f[j]*b.b[j][i]; return tmp; } friend wy operator ^(wy a,ll p) { wy tmp;tmp.f[0]=1; while(p) { if(p&1)tmp=tmp-a; p=p>>1; a=a*a; } return tmp; } }A,B; int main() { freopen("1.in","r",stdin); n=read();m=read();T=read();act=read();N=n*m; for(ll i=1;i<=n;++i)scanf("%s",ch[i]+1); for(ll i=1;i<=act;++i) { scanf("%s",c[i]+1); flag[i]=strlen(c[i]+1); } for(ll i=1;i<=n;++i)for(ll j=1;j<=m;++j)pos[i][j]=(i-1)*m+j; for(ll i=1;i<=n;++i) for(ll j=1;j<=m;++j) { ll target=ch[i][j]-'0'+1; for(ll k=1;k<=60;++k) { ll now=(k-1)%flag[target]+1; if(c[target][now]>='0'&&c[target][now]<='9') { a[k][pos[i][j]][pos[i][j]]=1; a[k][0][pos[i][j]]=c[target][now]-'0'; } if(c[target][now]=='E'&&j+1<=m)a[k][pos[i][j]][pos[i][j+1]]=1; if(c[target][now]=='W'&&j-1>=1)a[k][pos[i][j]][pos[i][j-1]]=1; if(c[target][now]=='N'&&i-1>=1)a[k][pos[i][j]][pos[i-1][j]]=1; if(c[target][now]=='S'&&i+1<=n)a[k][pos[i][j]][pos[i+1][j]]=1; } } nece=T/60;rest=T%60; for(ll k=1;k<=60;++k) { for(ll i=0;i<=N;++i) for(ll j=0;j<=N;++j)B.b[i][j]=a[k][i][j]; A.b[0][0]=B.b[0][0]=1; if(k==1)A=B; else A=A*B; } A.f[0]=1;A=A^(nece); for(ll k=1;k<=rest;++k) { for(ll i=1;i<=N;++i)B.f[i]=0; for(ll i=0;i<=N;++i) for(ll j=0;j<=N;++j)B.f[i]+=A.f[j]*a[k][j][i]; for(ll i=1;i<=N;++i)A.f[i]=B.f[i]; } for(ll i=1;i<=N;++i)maxx=max(maxx,A.f[i]); put(maxx); return 0; }
我是清都山水郎,天教分付与疏狂。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号