树上差分

　　差分 算是一种比较重要的操作了，而且 还简单 。

具体的 差分的好处 就是 O(1)时间内完成 区间操作 O(n)时间内得到区间总体答案。

假如不差分的话 那么每次区间操作都是O(n)的 最后 O(1)时间来提取答案。

整个操作是 O(n^2)的 而对于树上的差分操作 也是这样的。

这道题是一道简单的树上差分 练习题 主要是考察 对答案的产生地方的分析，

一条是原本的树上的边 另一条是新加的边。那么此时 对于一棵树多加一条边 产生的影响无疑是从x到 LCA 和y 到LCA这之间的边

形成了一个环对吧，我们可以说这时砍掉其中的一条树边 是不可能切断整张图的，那么此时 我们可以考虑切断一条新加的边，那不就是刚刚出现在x y之间的边么？

切掉这一条即可 但是如果被连了好多边呢，那这不就没用了么？是的这时答案肯定不会再被累加。

真正能累加答案的是只被覆盖一次和不被覆盖的树上的边。一条路径上的边都是被覆盖的那么可以利用树上差分 O(1)修改。

最后O(n) 输出答案即可。总复杂度O(n).

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define ll long long
#define INF 2147483647
#define x(i) t[i].x
#define y(i) t[i].y
#define mod 31011
#define R register
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(ll x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar(' ');return;
}
const int MAXN=100002;
int n,m;
ll ans;
int fa[MAXN],vis[MAXN],f[MAXN],lca[MAXN];//f[i]表示以i节点为根的子树往上被标记的次数
int lin[MAXN<<1],ver[MAXN<<1],nex[MAXN<<1],len;
vector<int>q[MAXN],q1[MAXN];
struct wy{int x,y;}t[MAXN];
inline void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
inline int getfather(int x){return x==fa[x]?x:fa[x]=getfather(fa[x]);}
void tarjan(int x)
{
    vis[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        tarjan(tn);
        vis[tn]=2;
        fa[tn]=x;
    }
    for(unsigned int i=0;i<q[x].size();++i)
    {
        int tn=q[x][i];
        if(vis[tn]==2)lca[q1[x][i]]=getfather(tn);
    }
    return;
}
void dfs(int x)
{
    vis[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        dfs(tn);
        f[x]+=f[tn];
    }
    if(x!=1)
    {
        if(f[x]==0)ans+=m;
        if(f[x]==1)++ans;
    }
    return;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<n;++i)
    {
        int x,y;fa[i]=i;
        x=read();y=read();
        add(x,y);add(y,x);
    }
    fa[n]=n;
    for(int i=1;i<=m;++i)
    {
        x(i)=read();
        y(i)=read();
        if(x(i)==y(i))continue;
        //cout<<x(i)<<' '<<y(i)<<endl;
        q[x(i)].push_back(y(i));
        q1[x(i)].push_back(i);
        q[y(i)].push_back(x(i));
        q1[y(i)].push_back(i);
    }
    memset(vis,0,sizeof(vis));
    tarjan(1);
    for(int i=1;i<=m;++i)
    {
        //put(lca[i]);
        if(x(i)==y(i))continue;
        ++f[x(i)];
        ++f[y(i)];
        f[lca[i]]-=2;
    }
    memset(vis,0,sizeof(vis));
    dfs(1);
    put(ans);
    return 0;
}

友情提醒 倍增求LCA 不会有坑点 x==y时有LCA 但是倍增求的话必须要特判这点注意！！！

这道题也是比较有意思的题目，因为 这不像一些树上的题目求根节点到当前节点的最大值什么的需要dfs序建线段树

这是随意从树中选出两个节点然后进行路径上的需改 我们早就习以为常了吧 差分一下 到分f[LCA]的时候差分效果消失即可。

然后考虑怎么维护答案 最多的救济粮  这不是线段树干的事情么可是维护的是次数并非救济粮自身的性质。考虑权值线段树

然后空间要GG 随便动态开点一下 然后也可以 进行线段树的合并啦！！！

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define ll long long
#define INF 2147483646
#define R register
#define r(i) t[i].r
#define l(i) t[i].l
#define sum(i) t[i].sum
#define v(i) t[i].v
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const int MAXN=100002;
int n,m,cnt,num;
int lin[MAXN<<1],ver[MAXN<<1],nex[MAXN<<1],len;
int a[MAXN],b[MAXN],f[MAXN],fa[MAXN],lca[MAXN],s[MAXN],s1[MAXN],vis[MAXN],root[MAXN],ans[MAXN];
vector<int>q[MAXN],q1[MAXN];
struct wy
{
    int l,r;
    int sum;//次数
    int v;//价值
}t[MAXN<<6];
inline void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
inline void discrete()
{
    sort(b+1,b+1+m);
    for(int i=1;i<=m;++i)if(i==1||b[i]!=b[cnt])b[++cnt]=b[i];
    for(int i=1;i<=m;++i)a[i]=lower_bound(b+1,b+1+cnt,a[i])-b;
}
inline int getfather(int x){return x==f[x]?x:f[x]=getfather(f[x]);}
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
inline void tarjan(int x)
{
    vis[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        tarjan(tn);
        f[tn]=x;
        fa[tn]=x;
        vis[tn]=2;
    }
    for(unsigned int i=0;i<q[x].size();++i)
    {
        int tn=q[x][i];
        if(vis[tn]==2)lca[q1[x][i]]=getfather(tn);
    }
    return;
}
inline void change(int &p,int l,int r,int x,int d)
{
    if(p==0)p=++num;
    if(l==r){sum(p)+=d,v(p)=l;return;}
    int mid=(l+r)>>1;
    if(x<=mid)change(l(p),l,mid,x,d);
    else change(r(p),mid+1,r,x,d);
    /*if(sum(l(p))==sum(r(p)))v(p)=min(v(l(p)),v(r(p)));
    else
    {
        if(sum(l(p))>sum(r(p)))v(p)=v(l(p));
        else v(p)=v(r(p));
    }
    sum(p)=max(sum(l(p)),sum(r(p)));*/
    sum(p)=max(sum(l(p)),sum(r(p)));
    v(p)=sum(l(p))>=sum(r(p))?v(l(p)):v(r(p));
    return;
}
inline int merge(int x,int y,int l,int r)
{
    if(x==0||y==0)return x+y;
    if(l==r){sum(x)+=sum(y);return x;}
    int mid=(l+r)>>1;
    l(x)=merge(l(x),l(y),l,mid);
    r(x)=merge(r(x),r(y),mid+1,r);
    /*if(sum(l(x))==sum(r(x)))v(x)=min(v(l(x)),v(r(x)));
    else
    {
        if(sum(l(x))>sum(r(x)))v(x)=v(l(x));
        else v(x)=v(r(x));
    }
    sum(x)=max(sum(l(x)),sum(r(x)));*/
    sum(x)=max(sum(l(x)),sum(r(x)));
    v(x)=sum(l(x))>=sum(r(x))?v(l(x)):v(r(x));
    return x;
}
inline void dfs(int x)
{
    vis[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        dfs(tn);
        root[x]=merge(root[x],root[tn],1,cnt);
    }
    if(sum(root[x])==0)ans[x]=0;
    else ans[x]=v(root[x]);
    return;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<n;++i)
    {
        int x,y;f[i]=i;
        x=read();y=read();
        add(x,y);add(y,x);
    }
    f[n]=n;
    for(int i=1;i<=m;++i)
    {
        s[i]=read();s1[i]=read();
        a[i]=b[i]=read();
        if(s[i]==s1[i]){lca[i]=s[i];continue;}
        q[s[i]].push_back(s1[i]);
        q1[s[i]].push_back(i);
        q[s1[i]].push_back(s[i]);
        q1[s1[i]].push_back(i);
    }
    discrete();
    tarjan(1);
    //put(cnt);for(int i=1;i<=m;++i)put(a[i]);
    //for(int i=1;i<=m;++i)put(lca[i]);
    for(int i=1;i<=m;++i)
    {
        change(root[s[i]],1,cnt,a[i],1);
        change(root[s1[i]],1,cnt,a[i],1);
        //cout<<b[v(root[s[i]])]<<' '<<b[a[i]]<<' '<<a[i]<<endl;
        change(root[lca[i]],1,cnt,a[i],-1);
        if(fa[lca[i]])change(root[fa[lca[i]]],1,cnt,a[i],-1);
    }
    //for(int i=1;i<=n;++i)put(b[v(root[i])]);
    memset(vis,0,sizeof(vis));
    dfs(1);
    for(int i=1;i<=n;++i)put(b[ans[i]]);
    return 0;
}

友情提示：tarjan 求LCA x==y时必须特判！！！不特判要跪。。

这题目算是2016年NOIP最难的题目了吧 的确很难 因为很难建模。。

我觉得这道题有点难想因为建模的过程比较难吧，问题转化好了将会非常简单。
首先我们考虑暴力 很多部分分。

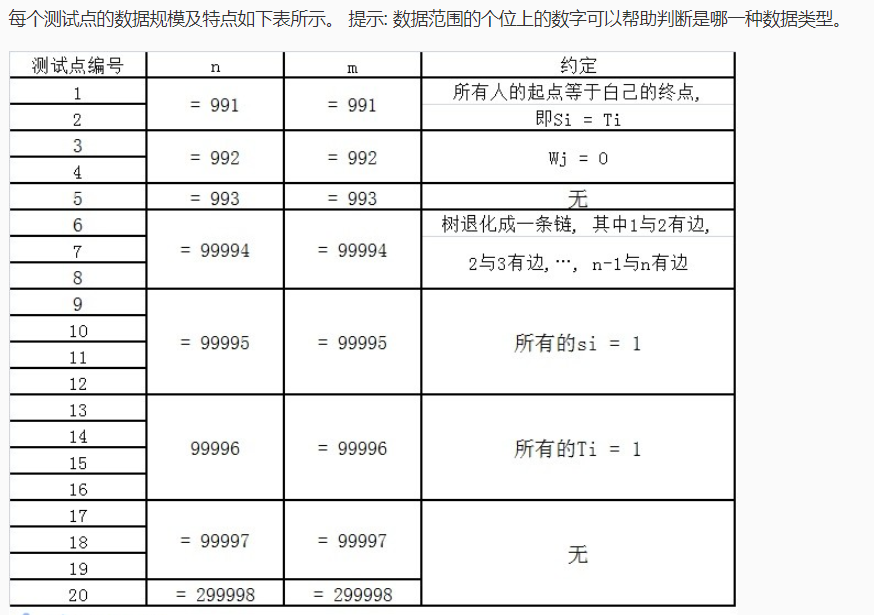
这么多的数据 还加上提示 怕不是出题人是以为我们看不见部分分吧 真的很良心啊。

1 2 直接秒了啊，算了 我能想到的暴力也只有暴力dfs q次即可这时 只能get一点分  还有一些分数可以bfs好像（我口胡的）

关键不是这个 怎么搞正解啊，很难吧，参考了一波书上的建模瞬间秒懂 转换问题和分解问题是关键。

还是考虑如何累计答案 当然是考虑 d[x] ->d[LCA] 的路径上 如果有点是合法的那么有等式 d[x]-d[p]==w[p] 

d[y]->d[LCA] d[x]+d[p]-(d[LCA]<<1)==w[p] 这时 p是任意节点 且p在x->y的最短路径上。其中d树改节点深度

等式 d[x]==w[p]+d[p]  d[x]-(d[LCA]<<1)==w[p]-d[p] 这其实等价于我们在 x y上分别分配 d[x] d[x]-(d[LCA]<<1)

然后查询w[p]+d[p] w[p] -d[p]的值了 考虑差分啊 第一个在x出效果在 f[LCA] 处消失 第二个则在LCA处消失因为避免重复 

下标为负考虑离散或整体迁移（推荐）离散操作难度太大且常数很大，考虑整体迁移。

注意：tarjan求LCA时必须特判这道题还特殊 特判完不能continue！！！

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define ll long long
#define INF 2147483646
#define R register
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=0;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getc();}
    return f?-x:x;
}
inline void put(int x)
{
    x<0?putchar('-'),x=-x:0;
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+'0',x/=10;
    num==0?putchar('0'):0;
    while(num)putchar(ch[num--]);
    putchar(' ');return;
}
const int MAXN=600002;
int n,m,cnt,num;
int f[MAXN],fa[MAXN],lca[MAXN],w[MAXN],depth[MAXN],s1[MAXN],s2[MAXN];
int c[MAXN<<1],c1[MAXN<<1],ans[MAXN],vis[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],len;
vector<int>q[MAXN],q1[MAXN],q2[MAXN],p[MAXN],a[MAXN],b[MAXN];

inline int getfather(int x){return x==f[x]?x:f[x]=getfather(f[x]);}

inline void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}

inline void tarjan(int x)
{
    vis[x]=1;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        depth[tn]=depth[x]+1;
        tarjan(tn);
        vis[tn]=2;
        f[tn]=x;fa[tn]=x;
    }
    for(unsigned int i=0;i<q1[x].size();++i)
    {
        int tn=q1[x][i];
        if(vis[tn]==2)lca[q2[x][i]]=getfather(tn);
    }
    return;
}

inline void dfs(int x)
{
    vis[x]=1;
    int sum=c[w[x]+depth[x]],sum1=c1[w[x]-depth[x]+n];
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==1)continue;
        dfs(tn);
    }
    for(unsigned int i=0;i<q[x].size();++i)++c[q[x][i]];
    for(unsigned int i=0;i<p[x].size();++i)--c[p[x][i]];
    for(unsigned int i=0;i<a[x].size();++i)++c1[a[x][i]+n];
    for(unsigned int i=0;i<b[x].size();++i)--c1[b[x][i]+n];
    ans[x]=c[w[x]+depth[x]]-sum+c1[w[x]-depth[x]+n]-sum1;
    return;
}

int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<n;++i)
    {
        int x,y;
        x=read();y=read();
        add(x,y);add(y,x);
    }
    for(int i=1;i<=n;++i)w[i]=read(),f[i]=i;
    for(int i=1;i<=m;++i)
    {
        int x,y;
        x=read();y=read();
        s1[i]=x;s2[i]=y;
        if(x==y)lca[i]=x;
        q1[x].push_back(y);
        q1[y].push_back(x);
        q2[x].push_back(i);
        q2[y].push_back(i);
     }
    tarjan(1);
    //for(int i=1;i<=n;++i)put(depth[i]);
    //for(int i=1;i<=m;++i)put(lca[i]);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        x=s1[i];y=s2[i];
        int father=lca[i];
        q[x].push_back(depth[x]);
        if(fa[father])p[fa[father]].push_back(depth[x]);
        a[y].push_back(depth[x]-depth[father]*2);
        b[father].push_back(depth[x]-depth[father]*2);
    }
    memset(vis,0,sizeof(vis));
    dfs(1);
    for(int i=1;i<=n;++i)put(ans[i]);
    return 0;
}

这样这道题就被完成了！

几段唏嘘几世悲欢 可笑我命由我不由天！