分块总结
尽管分块非常简单 但是它比其他数据结构更不好应用上去 。
也就是说可以巧妙的采用分块的思想 来优化时间 一般都是将n 优化到sqrt(n);
面对题目 我们总是会想办法转换模型 或者如果是一种算法的应用的话我们应该观察问题的特异性。
这道题显然 如果求每个磁石能吸引的块数的话 这 不就是个二维偏序么 可是求总共能吸引的磁石个数。
这就不太行了 二维偏序 当然也许可以暴力的时候写个二维偏序 拓扑序 bitset 或一下 最后 f[0].count()就是答案。
复杂度是比较高的。那再转换模型 这不就是一个bfs吧。n^2的bfs超级好写。
可是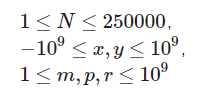
这个数据范围 卡爆bfs 想办法将其优化 我们把它按第一关键字排序分块 那么每次都会有一个界限 。
这样我们只用管这个界限之前的就可以了，和这个界限之后的第一个块。再对每个块进行第二关键字排序。
那么此时 每次第二关键字不满足就可以直接break 平均每次 被扫到均摊O(1)对于答案的选取。
我建议直接统计答案不要用队列中的t 因为我不知道自己为什么会一直wa 我觉得没有任何的问题。。
//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define db double #define x(i) s[i].x #define y(i) s[i].y #define f(i) s[i].force #define m(i) s[i].m #define r(i) s[i].r #define dis(i) s[i].dis using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=250002,maxn=1000; int n,c,p,s1,s2,T,len,ans; int q[MAXN],t,h; int l[maxn],r[maxn],flag[maxn],v[maxn],vis[MAXN]; struct wy { int x,y; int m,force,r; double dis; }s[MAXN]; inline double d(int t,int t1,int t2,int t3){return sqrt(((int)(t-t2)*(t-t2))*1.0+((int)(t1-t3)*(t1-t3))*1.0);} inline int cmp(wy x,wy y){return x.m<y.m;} inline double cmp1(wy x,wy y){return x.dis<y.dis;} void bfs() { t=1,h=0; while(++h<=t) { int last; if(h!=1)c=r(q[h]),p=f(q[h]); for(int i=1;i<=T;++i) { if(v[i]<=p) for(int j=flag[i];j<=r[i];++j) { //if(vis[j]==1)continue; if(dis(j)<=c){q[++t]=j,++flag[i];if(vis[j]==0)ans++,vis[j]=1;} //直接统计答案为好 不然还是wa else break; } else {last=i;break;} } for(int i=flag[last];i<=r[last];++i) { //if(vis[i]==1)continue; if(m(i)<=p) { if(dis(i)<=c) { q[++t]=i; if(vis[i]==0)ans++,vis[i]=1; } else break; } } } } int main() { //freopen("1.in","r",stdin); s1=read();s2=read(); p=read();c=read(); n=read(); for(int i=1;i<=n;++i) { x(i)=read();y(i)=read(); m(i)=read();f(i)=read(); r(i)=read();dis(i)=d(s1,s2,x(i),y(i)); } sort(s+1,s+1+n,cmp); T=(int)sqrt(n*1.0);len=n/T; //for(int i=1;i<=n;i++)cout<<dis(i)<<endl; for(int i=1;i<=T;++i) { l[i]=(i-1)*len+1; r[i]=len*i; flag[i]=l[i]; v[i]=m(r[i]); sort(s+l[i],s+r[i]+1,cmp1); } if(r[T]<n) { ++T,l[T]=r[T-1]+1,r[T]=n; v[T]=m(r[T]); sort(s+l[T],s+r[T]+1,cmp1); flag[T]=l[T]; } //for(int i=1;i<=n;i++)cout<<dis(i)<<' '<<m(i)<<' '<<f(i)<<' '<<r(i)<<endl; bfs(); put(ans); return 0; }
这道题是书上讲的 用分块进行分治 这种分治答案非常的典型 也是很多用不了单调队列的题目优化的模型方法之一非常值得借鉴。
直接把n^2的算法利用单调性优化到nsqrt(n)这样 成功完美解决一道莫队的题目！
记得以前写的维护一些区间的性质 例如求某个区间的最大值ST算法。。
当时我是用单调队列扫 然后发现一个另一个端点不具单调性 此时我们可以也是这道题的解法：
将其按照第一关键字排序 然后 分块 分成 sqrt(m) 块的大小为sqrt(m)
对于每个块中的元素 我们按照第二关键字排序对于每个块之中 第二关键字是单调递增的。
第一关键字 每次改变幅度是sqrt(n)的 考虑如果不是根号n的 那么也影响不大 复杂度 nsqrt(n).
至于每次第二关键字的变化幅度一定是 sqrt(n)的 不懂的话 我用了反证法证明这个问题。
关键是 均摊复杂度 非常优秀 nsqrt(n) 还有很关键的是 每次选择的基准块很不错导致复杂度骤降。
//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define db double #define x(i) t[i].x #define y(i) t[i].y #define id(i) t[i].id using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; ll num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); return; } const ll MAXN=50002; struct wy { ll x,y; ll id; }t[MAXN]; ll n,m,T,len,num; ll x[MAXN],y[MAXN],l[MAXN],r[MAXN]; ll a[MAXN],cnt[MAXN],ans;// molecular 分子 denominator分母 ll cmp(wy x,wy y){return x.x<y.x;} ll cmp1(wy x,wy y){return x.y<y.y;} ll cmp2(wy x,wy y){return x.id<y.id;} ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);} void curculate() { for(ll k=1;k<=T;++k) { ans=0; memset(cnt,0,sizeof(cnt)); ll R=y(l[k]),L=x(l[k]);//右端点单调递增 for(ll i=L;i<=R;++i) { ++cnt[a[i]]; if(cnt[a[i]]>1)ans=ans-(cnt[a[i]]-1)*(cnt[a[i]]-2)/2+cnt[a[i]]*(cnt[a[i]]-1)/2; } x[id(l[k])]=ans; for(ll i=l[k]+1;i<=r[k];++i) { if(x(i)==y(i)){x[id(i)]=0;continue;} if(R<y(i)) for(ll j=R+1;j<=y(i);++j) { ++cnt[a[j]]; if(cnt[a[ j]]>1)ans=ans-(cnt[a[j]]-1)*(cnt[a[j]]-2)/2+cnt[a[j]]*(cnt[a[j]]-1)/2; } if(L<x(i)) for(ll j=L;j<x(i);++j) { --cnt[a[j]]; if(cnt[a[j]]>0)ans=ans-(cnt[a[j]]+1)*cnt[a[j]]/2+cnt[a[j]]*(cnt[a[j]]-1)/2; } if(L>x(i)) for(ll j=L-1;j>=x(i);--j) { ++cnt[a[j]]; if(cnt[a[j]]>1)ans=ans-(cnt[a[j]]-1)*(cnt[a[j]]-2)/2+cnt[a[j]]*(cnt[a[j]]-1)/2; } x[id(i)]=ans; L=x(i);R=y(i); } } } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(ll i=1;i<=n;++i)a[i]=read(); for(ll i=1;i<=m;++i) { x(i)=read(); y(i)=read(); id(i)=i; } sort(t+1,t+1+m,cmp); T=(ll)sqrt(m*1.0);len=m/T; for(ll i=1;i<=T;++i) { l[i]=(i-1)*len+1; r[i]=len*i; sort(t+l[i],t+r[i]+1,cmp1); } if(r[T]<m) { ++T,l[T]=r[T-1]+1,r[T]=m; sort(t+l[T],t+r[T]+1,cmp1); } curculate(); sort(t+1,t+1+m,cmp2); for(ll i=1;i<=m;i++) { if(x[i]==0)puts("0/1"); else { ll w=(y(i)-x(i)+1)*(y(i)-x(i))/2; ll g=gcd(w,x[i]); put(x[i]/g),putchar('/'),put(w/g),puts(""); } } return 0; }
