线段树的高级操作
明明知道 这样下去会崩盘 我还在尽量维护和文化课之间的关系 尽管省选是学长们重要的事情,但是 我可不想是一个打酱油的
不管是为了今年的NOIP 还是 我对代码的热情 我都必须这样做 。他们 ,爱怎么说怎么说吧。我要去远方,且从不后退。

一眼看出来是线段树 但是需要离散 好像动态开点线段树应该也是不行的吧。
但是关键的不是线段树+离散化有多不好写 (离散写了20min才知道怎么写)
是最后的条件判断这个相当的有意思呢 必真必假 还是maybe
写完后看题解才知道自己判断的方法相当的不好 题解上给的策略是这样的先判断优先级最高的false
再接着判断 maybe 最后剩下的一定是true 了。
我的策略也算可以只不过比较麻烦 如下先判断两个点是否重合进行情况比较
再判断 x是否==y+1 再进行情况比较
最后 x y中有很多的年时在进行情况比较 这样就完成了 比较麻烦 第一次提交0分 因为每考虑好
第二次70分 因为有一些坑点 比如 x==y时如果x是已知的就是true 未知就是maybe 搞不懂为什么会这样。。。都是true不好吗?坑点
最后终于AC 注意本校OJ 有坑点 x y 有0的出现
值得一提是对于区间是否有未知的只需判断区间长度是否等于离散后的区间长度即可 而我又再次采用了较笨的方法。。。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<cctype> #include<utility> #include<ctime> #include<queue> #include<deque> #include<stack> #include<vector> #include<set> #include<bitset> #include<cstring> #include<string> #include<algorithm> #define l(x) t[x].l #define r(x) t[x].r #define sum(x) t[x].sum #define p(x) t[x].p using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(10);return; } const int MAXN=100002; int n,m,x[MAXN],y[MAXN]; int a[MAXN],w[MAXN],cnt,num,sum; int b[MAXN],c[MAXN],s[MAXN]; bool flag; struct wy { int l,r; int p;//是否有未知信息 int sum;//区间最大值 }t[MAXN<<2]; inline int max(int x,int y){return x>y?x:y;} void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r){p(p)=s[l]==0?1:0;sum(p)=s[l]==0?0:s[l];return;} int mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); sum(p)=max(sum(p<<1),sum(p<<1|1)); p(p)+=p(p<<1)+p(p<<1|1); } void discrete() { sort(b+1,b+1+cnt); for(int i=1;i<=cnt;i++)if(i==1||b[i]!=b[i-1])b[++sum]=b[i]; c[++num]=b[1]; for(int i=2;i<=sum;i++) { if(b[i-1]+1!=b[i])c[++num]=b[i-1]+1; c[++num]=b[i]; } } int ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p)) { if(p(p)>0)flag=1; return sum(p); } int mid=(l(p)+r(p))>>1; int cnt=0; if(l<=mid)cnt=max(cnt,ask(p<<1,l,r)); if(r>mid)cnt=max(cnt,ask(p<<1|1,l,r)); return cnt; } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); w[i]=read(); b[++cnt]=a[i]; } m=read(); for(int i=1;i<=m;i++) { x[i]=read();y[i]=read(); b[++cnt]=x[i]; b[++cnt]=y[i]; } discrete();cnt=0;sum=0; for(int i=1;i<=n;i++) { a[i]=lower_bound(c+1,c+1+num,a[i])-c; s[a[i]]=w[i]; } //for(int i=1;i<=num;i++)cout<<s[i]<<endl; //for(int i=1;i<=n;i++)cout<<lower_bound(c+1,c+1+num,a[i])-c<<endl; //put(num); build(1,1,num); //put(p(1)); for(int i=1;i<=m;i++)//按照有序的判定容易AC { flag=0; int xx=lower_bound(c+1,c+1+num,x[i])-c; int yy=lower_bound(c+1,c+1+num,y[i])-c; if(xx>yy){puts("false");continue;} if(xx==yy&&s[xx]==0){puts("maybe");continue;}//坑点 if(xx==yy&&s[xx]!=0){puts("true");continue;}//坑点 if(xx+1==yy) { if(s[xx]==0){puts("maybe");continue;} if(s[yy]==0){puts("maybe");continue;} if(s[xx]==0&&s[yy]==0){puts("maybe");continue;} if(s[yy]>s[xx]){puts("false");continue;} puts("true");continue; } int answer=ask(1,xx+1,yy-1); if(s[xx]==0&&s[yy]==0){puts("maybe");continue;} if(s[xx]==0) { if(s[yy]>answer)puts("maybe"); else puts("false"); continue; } if(s[yy]==0) { if(s[xx]>answer)puts("maybe"); else puts("false"); continue; } if(s[yy]>s[xx]){puts("false");continue;} if(answer==0){puts("maybe");continue;} if(answer>=s[xx]){puts("false");continue;} if(answer>=s[yy]){puts("false");continue;} if(flag==1){puts("maybe");continue;} puts("true"); if(i==34)cout<<x[i]<<' '<<y[i]<<endl; } return 0; }

求区间连续最大和且带单点修改 (区间修改我想线段树应该是完不成的)
怎么维护区间连续喝最大呢我们需要多维护一些元素
lx 表示紧靠区间左边的max rx 表示紧靠区间右边的max 我们只需要求出区间的总体最大值即可。
这样就可以进行维护了。cnt.v=max(lx.v,max(rx.v,lx.rx+rx.lx));
然后值得一提的是最后回答询问就比较有意思了想了很久还是不知道如何写。
我知道最后一定可以转换成一个区间和 左边 和 右边
然后不知道如何书写 其实是这样的在返回时返回一个结构体值 具体细节看code

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<cctype> #include<utility> #include<ctime> #include<queue> #include<deque> #include<stack> #include<vector> #include<set> #include<bitset> #include<cstring> #include<string> #include<algorithm> #define INF 2147483646 #define l(x) t[x].l #define r(x) t[x].r #define sum(x) t[x].sum #define lx(x) t[x].lx #define rx(x) t[x].rx #define v(x) t[x].v using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(10);return; } const int MAXN=500002; int n,m; struct wy { int l,r; int lx,rx;//lx紧靠左边的最大值 rx紧靠右边的最大值 int sum,v;//sum代表区间和v代表当前区间最大连续字段和 }t[MAXN<<2]; int a[MAXN]; inline int max(int x,int y){return x>y?x:y;} void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r){lx(p)=a[l];rx(p)=a[r];sum(p)+=a[l];v(p)=a[l];return;} int mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); sum(p)=sum(p<<1)+sum(p<<1|1); lx(p)=max(lx(p<<1),sum(p<<1)+lx(p<<1|1)); rx(p)=max(rx(p<<1|1),sum(p<<1|1)+rx(p<<1)); v(p)=max(v(p<<1),max(v(p<<1|1),rx(p<<1)+lx(p<<1|1))); } void change(int p,int l,int d) { if(l(p)==l&&l==r(p)){sum(p)=d;lx(p)=d;rx(p)=d;v(p)=d;return;} int mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,d); else change(p<<1|1,l,d); sum(p)=sum(p<<1)+sum(p<<1|1); lx(p)=max(lx(p<<1),sum(p<<1)+lx(p<<1|1)); rx(p)=max(rx(p<<1|1),sum(p<<1|1)+rx(p<<1)); v(p)=max(v(p<<1),max(v(p<<1|1),rx(p<<1)+lx(p<<1|1))); } wy ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p))return t[p]; int mid=(l(p)+r(p))>>1; if(l>mid)return ask(p<<1|1,l,r); if(r<=mid)return ask(p<<1,l,r); wy lx,rx,cnt; lx=ask(p<<1,l,r);rx=ask(p<<1|1,l,r); cnt.sum=lx.sum+rx.sum; cnt.lx=max(lx.lx,lx.sum+rx.lx); cnt.rx=max(rx.rx,rx.sum+lx.rx); cnt.v=max(lx.v,max(rx.v,lx.rx+rx.lx)); return cnt; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++)a[i]=read(); build(1,1,n); //cout<<v(1)<<endl; for(int i=1;i<=m;i++) { int p,x,y,u; p=read();x=read();y=read(); if(p==1){if(x>y)u=x,x=y,y=u;put(ask(1,x,y).v);} else change(1,x,y); } return 0; }

这道题就很有意思了 基本线段树的操作就看你如何转换问题了。
求 区间修改 单调查询 如何整成一个区间呢 dfs序即可解决这个问题。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<cctype> #include<utility> #include<ctime> #include<queue> #include<deque> #include<stack> #include<vector> #include<set> #include<bitset> #include<cstring> #include<string> #include<algorithm> #define l(x) t[x].l #define r(x) t[x].r #define v(x) t[x].v #define k(x) t[x].k #define add1(x) t[x].add1 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(int x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(10);return; } const int MAXN=500002; int n,m,root=1,cnt; int lin[MAXN],nex[MAXN],ver[MAXN],len=0; int v[MAXN],l[MAXN],r[MAXN],vis[MAXN<<1]; char a[3]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } struct wy { int l,r; int v; int k;//属性 int add1; }t[(MAXN<<1)<<2]; void dfs(int x) { l[x]=++cnt;vis[cnt]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; dfs(tn); } r[x]=++cnt; } void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r){k(p)=(vis[l]==1?1:-1);return;} int mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); k(p)=k(p<<1)+k(p<<1|1); } void pushdown(int p) { add1(p<<1)+=add1(p); add1(p<<1|1)+=add1(p); v(p<<1)+=k(p<<1)*add1(p); v(p<<1|1)+=k(p<<1|1)*add1(p); add1(p)=0; return; } void change(int p,int l,int r,int d) { if(l<=l(p)&&r>=r(p)) { v(p)+=k(p)*d; add1(p)+=d; return; } if(add1(p))pushdown(p); int mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,r,d); if(r>mid)change(p<<1|1,l,r,d); return; } int ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p))return v(p); if(add1(p))pushdown(p); int cnt=0; int mid=(l(p)+r(p))>>1; if(l<=mid)cnt+=ask(p<<1,l,r); if(r>mid)cnt+=ask(p<<1|1,l,r); return cnt; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); v[1]=read(); for(int i=2;i<=n;i++) { int x; v[i]=read();x=read(); add(x,i); } dfs(root); //for(int i=1;i<=n;i++)cout<<l[i]<<' '<<r[i]<<endl; build(1,1,cnt); //for(int i=1;i<=cnt;i++)cout<<vis[i]<<endl; for(int i=1;i<=m;i++) { int x,y; scanf("%s",a+1); if(a[1]=='p') { x=read();y=read(); change(1,l[x]+1,r[x]-1,y); } else { x=read(); put(ask(1,l[x],l[x])+v[x]); } } return 0; }

这个问题是 求当前节点到根节点的距离 也是很好求的。dfs序一转化即可。

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<cctype> #include<utility> #include<ctime> #include<queue> #include<deque> #include<stack> #include<vector> #include<set> #include<bitset> #include<cstring> #include<string> #include<algorithm> #define l(x) t[x].l #define r(x) t[x].r #define v(x) t[x].v #define k(x) t[x].k #define add1(x) t[x].add1 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(int x) { x<0?x=-x,putchar('-'):0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(10);return; } const int MAXN=100002; int n,m,root=1,cnt; int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],len=0; int l[MAXN],r[MAXN]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } struct wy { int l,r; int k;//属性 }t[(MAXN<<1)<<2]; void dfs(int x,int father) { l[x]=++cnt; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(tn==father)continue; dfs(tn,x); } r[x]=++cnt; } void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r)return; int mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); } void change(int p,int l,int d) { if(l(p)==l&&r(p)==l){k(p)=d;return;} int mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,d); else change(p<<1|1,l,d); k(p)=k(p<<1)+k(p<<1|1); return; } int ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p))return k(p); int cnt=0; int mid=(l(p)+r(p))>>1; if(l<=mid)cnt+=ask(p<<1,l,r); if(r>mid)cnt+=ask(p<<1|1,l,r); return cnt; } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=1;i<n;i++) { int x,y; x=read();y=read(); add(x,y);add(y,x); } dfs(root,0); //for(int i=1;i<=n;i++)cout<<l[i]<<' '<<r[i]<<endl; build(1,1,cnt); for(int i=1;i<=n;i++) { int x; x=read(); put(ask(1,1,l[x])); change(1,l[x],1); change(1,r[x],-1); } return 0; }
不要把dfs序想的太难画一棵树 看看它的序列进行操作会进行怎么神奇的效果!
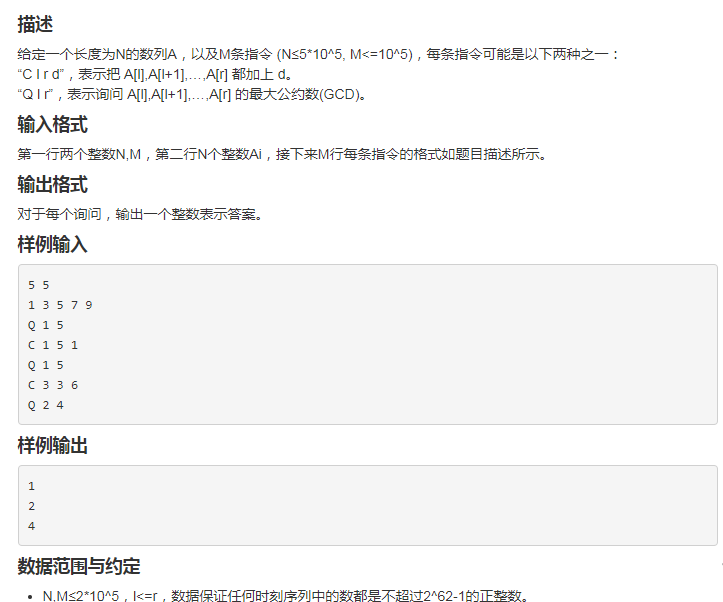
这道题超级巧妙QAQ 写出来后把我激动的 真的是线段树超高级操作
维护区间的GCD 且还带区间修改这个写暴力 早T飞了吧
线段树能维护! 根据更相减损法 gcd(x,y,z)=gcd(x,y-x,z-y);你只需证明这个等式的正确性即可 。
显然正确啊 线段树维护这个差分序列的GCD即可。。
这时先不急怎么写 考虑差分后的数组如果是负数怎么办 那么此时我证明了一下把负数变成正数的差分值最大公约数也是一样的 毕竟不证明很不爽啊。
然后 就可以维护了啊。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define l(x) t[x].l #define r(x) t[x].r #define g(x) t[x].g using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline long long read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(long long x) { x<0?putchar('-'),x=-x:0; long long num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const long long MAXN=500002; long long n,m; long long a[MAXN],c[MAXN]; char b[2]; struct wy { long long l,r; long long g; }t[MAXN<<2]; inline long long gcd(long long a,long long b) { if(a<0)a=-a;if(b<0)b=-b; if(a==0||b==0)return a+b; if(a>b)return gcd(b,a%b); else return gcd(a,b%a); } void build(long long p,long long l,long long r) { l(p)=l;r(p)=r; if(l==r){g(p)=a[l]-a[l-1];return;} long long mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); g(p)=gcd(g(p<<1),g(p<<1|1)); } void add(long long x,long long y){for(;x<=n;x+=x&(-x))c[x]+=y;} long long ask1(long long x) { long long cnt=0; for(;x;x-=x&(-x))cnt+=c[x]; return cnt; } long long ask(long long p,long long l,long long r) { if(l<=l(p)&&r>=r(p))return t[p].g; long long mid=(l(p)+r(p))>>1; long long cnt=0; if(l<=mid)cnt=gcd(cnt,ask(p<<1,l,r)); if(r>mid)cnt=gcd(cnt,ask(p<<1|1,l,r)); return cnt; } void change(long long p,long long l,long long d) { if(l==l(p)&&r(p)==l){g(p)+=d;return;} long long mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,d); else change(p<<1|1,l,d); g(p)=gcd(g(p<<1),g(p<<1|1)); } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(long long i=1;i<=n;i++)a[i]=read(); build(1,1,n); for(long long i=1;i<=m;i++) { long long x,y,d; scanf("%s",b+1); x=read();y=read(); if(b[1]=='Q') { long long ans=ask1(x)+a[x],ans1=0;x++; if(x<=y)ans1=ask(1,x,y); put(gcd(ans,ans1)); } else { d=read(); change(1,x,d); add(x,d); if(y+1>n)continue; change(1,y+1,-d); add(y+1,-d); } } return 0; }
真是巧妙的转换 之所以这样转换的原因呢? 因为 可以把区间修改在差分数组上 体现成为 单点修改。。

这道题是我见过的最不好写的题目了显然线段树维护。
要维护的信息很多如果开多个变量的话 会把自己写的恶心。。
就像我直接写8,9个元素需要同时维护 很不好写。瞄了一眼题解发现可以开成2维的瞬间好写了一点。
然后就可以开始码了都是基本操作吧 注意优先级即可。
注意pushdown 的位置因为这个我调了一下午。。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define l(x) t[x].l #define r(x) t[x].r #define lx(x) t[x].lx #define rx(x) t[x].rx #define seq(x) t[x].seq #define add(x) t[x].add #define sum(x) t[x].sum #define re(x) t[x].re #define z p<<1 #define y p<<1|1 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=100002; struct wy { int l,r; int sum;//维护区间有多少个1 int seq[2];//sequence 序列 维护序列中最长的01的序列 int lx[2],rx[2];//维护左右端点最长的01序列 int add;//维护序列是否全部赋值为0 或1 或不进行操作-1 int re;//reversal翻转逆转 维护序列是否翻转0 不翻转 1翻转 }t[MAXN<<2]; int n,m; int a[MAXN]; inline int max(int x,int w){return x>w?x:w;} inline void swap(int &x,int &w){int t;t=x;x=w;w=t;} void build(int p,int l,int r) { l(p)=l;r(p)=r; if(l==r) { lx(p)[0]=a[l]==1?0:1;rx(p)[0]=lx(p)[0]; lx(p)[1]=lx(p)[0]^1;rx(p)[1]=lx(p)[1]; seq(p)[0]=lx(p)[0];seq(p)[1]=lx(p)[1]; sum(p)=lx(p)[1];add(p)=-1; return; } int mid=(l+r)>>1; build(z,l,mid); build(y,mid+1,r); for(int i=0;i<=1;i++) { lx(p)[i]=lx(z)[i]==(r(z)-l(z)+1)?lx(z)[i]+lx(y)[i]:lx(z)[i]; rx(p)[i]=rx(y)[i]==(r(y)-l(y)+1)?rx(y)[i]+rx(z)[i]:rx(y)[i]; seq(p)[i]=max(seq(z)[i],max(seq(y)[i],rx(z)[i]+lx(y)[i])); } sum(p)=sum(z)+sum(y);add(p)=-1; } void pushdown(int p) { if(add(p)!=-1) { int d=add(p); add(y)=add(z)=d;add(p)=-1; re(z)=re(y)=0; sum(z)=(r(z)-l(z)+1)*d; sum(y)=(r(y)-l(y)+1)*d; seq(z)[d]=lx(z)[d]=rx(z)[d]=(r(z)-l(z)+1); seq(y)[d]=lx(y)[d]=rx(y)[d]=(r(y)-l(y)+1); seq(z)[d^1]=lx(z)[d^1]=rx(z)[d^1]=0; seq(y)[d^1]=lx(y)[d^1]=rx(y)[d^1]=0; } if(re(p)) { int d=0; re(z)=re(z)^1;re(y)=re(y)^1;re(p)=0; sum(z)=(r(z)-l(z)+1)-sum(z); sum(y)=(r(y)-l(y)+1)-sum(y); swap(seq(z)[d],seq(z)[d^1]); swap(lx(z)[d],lx(z)[d^1]); swap(rx(z)[d],rx(z)[d^1]); swap(seq(y)[d],seq(y)[d^1]); swap(lx(y)[d],lx(y)[d^1]); swap(rx(y)[d],rx(y)[d^1]); } return; } void change(int p,int l,int r,int d) { if(l<=l(p)&&r>=r(p)) { if(d==0||d==1) { re(p)=0;add(p)=d; sum(p)=(r(p)-l(p)+1)*d; seq(p)[d]=lx(p)[d]=rx(p)[d]=(r(p)-l(p)+1); seq(p)[d^1]=lx(p)[d^1]=rx(p)[d^1]=0; } else { int x=0; re(p)=re(p)^1; sum(p)=(r(p)-l(p)+1)-sum(p); swap(seq(p)[x],seq(p)[x^1]); swap(lx(p)[x],lx(p)[x^1]); swap(rx(p)[x],rx(p)[x^1]); } return; } int mid=(l(p)+r(p))>>1; pushdown(p); if(l<=mid)change(z,l,r,d); if(r>mid)change(y,l,r,d); for(int i=0;i<=1;i++) { lx(p)[i]=lx(z)[i]==(r(z)-l(z)+1)?lx(z)[i]+lx(y)[i]:lx(z)[i]; rx(p)[i]=rx(y)[i]==(r(y)-l(y)+1)?rx(y)[i]+rx(z)[i]:rx(y)[i]; seq(p)[i]=max(seq(z)[i],max(seq(y)[i],rx(z)[i]+lx(y)[i])); } sum(p)=sum(z)+sum(y); } int ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p))return sum(p); int cnt=0; int mid=(l(p)+r(p))>>1; pushdown(p); if(l<=mid)cnt+=ask(z,l,r); if(r>mid)cnt+=ask(y,l,r); for(int i=0;i<=1;i++) { lx(p)[i]=lx(z)[i]==(r(z)-l(z)+1)?lx(z)[i]+lx(y)[i]:lx(z)[i]; rx(p)[i]=rx(y)[i]==(r(y)-l(y)+1)?rx(y)[i]+rx(z)[i]:rx(y)[i]; seq(p)[i]=max(seq(z)[i],max(seq(y)[i],rx(z)[i]+lx(y)[i])); } sum(p)=sum(z)+sum(y); return cnt; } wy query(int p,int l,int r)//query 疑问,质问;疑问号 询问 { if(l<=l(p)&&r>=r(p))return t[p]; int mid=(l(p)+r(p))>>1; pushdown(p); if(r<=mid)return query(z,l,r); if(l>mid)return query(y,l,r); wy a,b,c; a=query(z,l,mid); b=query(y,mid+1,r); c.seq[1]=max(a.seq[1],max(b.seq[1],a.rx[1]+b.lx[1])); c.lx[1]=a.lx[1]==(r(z)-l(z)+1)?r(z)-l(z)+1+b.lx[1]:a.lx[1]; c.rx[1]=b.rx[1]==(r(y)-l(y)+1)?r(y)-l(y)+1+a.rx[1]:b.rx[1]; for(int i=0;i<=1;i++) { lx(p)[i]=lx(z)[i]==(r(z)-l(z)+1)?lx(z)[i]+lx(y)[i]:lx(z)[i]; rx(p)[i]=rx(y)[i]==(r(y)-l(y)+1)?rx(y)[i]+rx(z)[i]:rx(y)[i]; seq(p)[i]=max(seq(z)[i],max(seq(y)[i],rx(z)[i]+lx(y)[i])); } sum(p)=sum(z)+sum(y); return c; } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++)a[i]=read(); build(1,1,n); //cout<<sum(1)<<endl;//cout<<lx(1)[0]<<endl; //cout<<rx(1)[1]<<endl;//cout<<seq(1)[1]<<endl; for(int i=1;i<=m;i++) { int p,x,k; p=read();x=read()+1;k=read()+1; switch(p) { case 0:change(1,x,k,0);//把[x,k]区间内的所有数全变成0 break; case 1:change(1,x,k,1);//把[x,k]区间内的所有数全变成0 break; case 2:change(1,x,k,2);//把[x,k]区间内的所有数取反 break; case 3:put(ask(1,x,k));//询问[x,k]区间内有多少个1 break; case 4:put(query(1,x,k).seq[1]);//询问区间内最长的连续的1的个数 break; } } //cout<<1<<endl; return 0; }
满堂惟有烛花红,杯且从容,歌且从容。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号