关于强联通分量 的求法讨论
这个讨论主要是关于 HA2006年最受欢迎的牛 的讨论 。
尽管这道题对于很多dalao来说都觉得是模板题,但是仍是值得思考的,因为我第一次写这道题的时候,
缩完点之后建图建错玄学跑dfs n^2做法仍是将这道题A掉了如今我很可怕,当时觉得很简单却被我的玄学做法水过了。
所以我认为应该仔细思考这道题的做法,因为我们直觉上的topsort 但是topsort貌似不行。
针对这道题显然 要求很多的超级汇点 怎么求呢?
我考虑 由于点很多我们不妨缩点 因为最后如果有多个超级汇点的话那么一定形成了一个环。
那么暴力呢?好像是有记搜的写法的我复杂度O(m+n)比较不错这还缩什么点?
写完后看了一眼题解 然后发现真的有n^2过10000的算法直接每个点暴力跑dfs 加上一些剪枝也是可以通过的。但是代码复杂度较高我懒得写。。
怎么缩点呢?割边 边双联通分量 缩点 我不太会,总感觉哪里有点不对。
求强联通分量之时 有几个问题:
首先 虽然这道题是一张有向图但是 貌似 无向图的割边能使用么?
这个想法看起来很没用,也的确没有任何意义 对于一张无向图一些不构成环的点自然是割边,没意义。
求强联通分量即可。那么割点呢?割边的两端有可能是割点对吧,那么割边要求的是自己的儿子 且有可能不止一个,割点一般要求的是如果不是根节点的话那么只要一个儿子足以。所以这里割点和割边在有向图中也根本没必要。
由上述分析我们可以再得出一个问题如果有重边的话那么对割边或割点有影响么?
对于割点的话它很显然是没有影响的,对于割边的话就有点影响了试想如果原本这条边是割边,那么重边加进去这条割边,那么此时这条割边将不再是割边了。
有点思考那么此时为了防止这种情况的发生我们可以成对变换,可以解决此类问题。
接下来的问题就是求强联通分量了,前面已经说了在有向图中如果一些点构不成环,那么剩下的不是环上的边都有都是割边,且此时缩点不好缩,且割边不易求。
放弃,直接强联通分量方便的多,上面的在有向图上割边缩点完全是无意义的做法,放弃。
那么话题重新回到这道题的身上,强联通的判定法则,如果当前点dfn[x]==low[n] 那么这个栈中从一些点到它自己都是联通分量。缩点就行了。
接下来我的思路是顺理成章的拓扑排序。那么这道题就陷入了怎么写都会挂的尴尬处境。
缩点之后的建图,大家肯定都会发现很有可能会重边什么的这对拓扑排序有非常大的影响,直接影响到了答案。
所以我们不能建重边,至于邻接表判重边这个错误的想法我真的不知道是怎么萌生的看来还是思考的时候思想不够成熟。
尽管有重边对于一个DAG,拓扑排序照样可以。真的是没有考虑清楚随便写了。
当然我曾经想过并查集维护不重边,然后GG了,当然 这并不尴尬因为就算维护了不重边那么拓扑排序也是失败。
一种写法 只要任何点到达当前的点那么当前点就加上其价值然后 最后和缩点个数减一判断即可,显然是错误的。
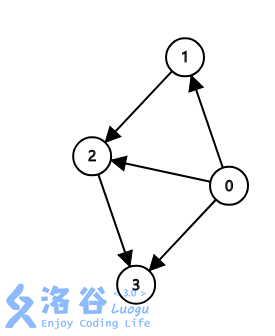
这样无论如何价值都会被累加多遍直接原地去世,然后这道题其实有一种更为巧妙的方法,就是数出度,如果有两个出度为0的点的话那么答案一定为0了
只有一个出度为0的点的话在一张DAG上那么这就是答案了。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cctype> #include<utility> #include<queue> #include<stack> #include<deque> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<ctime> #include<set> #include<bitset> #include<map> #include<cmath> #include<vector> #include<cstdlib> #define INF 2147483646 #define INF1 168430090 #define ll long long using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50002,maxn=10002; int n,m; int lin[MAXN],ver[MAXN],nex[MAXN],len=0; int clin[MAXN],cver[MAXN],cnex[MAXN],clen=0; int dfn[maxn],vis[maxn],low[maxn],num=0; int c[maxn],s[maxn],cnt,flag,ans,t,p; int f[maxn],sz[maxn],q[maxn],ru[maxn],h,dis[maxn]; int getfather(int x) { return x==f[x]?x:f[x]=getfather(f[x]); } void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void cadd(int x,int y) { cver[++clen]=y; cnex[clen]=clin[x]; clin[x]=clen; } void tarjan(int x) { dfn[x]=low[x]=++num; vis[x]=1;s[++t]=x; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(dfn[tn]==0) { tarjan(tn); low[x]=min(low[x],low[tn]); } else if(vis[tn]==1)low[x]=min(low[x],dfn[tn]); } if(dfn[x]==low[x]) { int y; cnt++; do { y=s[t--];vis[y]=0; c[y]=cnt;sz[cnt]++; } while(y!=x); //if(cnt==1)put(sz[cnt]); } } void bfs() { h=t=0; for(int i=1;i<=cnt;i++)if(ru[i]==0)q[++t]=i; //cout<<t<<endl; while(h++<t) { int te=q[h]; for(int i=clin[te];i;i=cnex[i]) { int tn=cver[i]; ru[tn]--; if(ru[tn]==0)q[++t]=tn,dis[tn]+=dis[te]+1; } } return; } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(int i=1;i<=m;i++) { int x,y; x=read();y=read(); add(x,y); } for(int i=1;i<=n;i++)if(dfn[i]==0)tarjan(i); //for(int i=1;i<=cnt;i++)cout<<sz[i]<<endl; //put(cnt); //for(int i=1;i<=cnt;i++)f[i]=i; for(int i=1;i<=n;i++) { for(int j=lin[i];j;j=nex[j]) { int tn=ver[j]; //int xx=getfather(c[i]); //int yy=getfather(c[tn]); //if(xx==yy)continue; if(c[i]==c[tn])continue; cadd(c[i],c[tn]);ru[c[i]]++; //f[xx]=yy; } } //for(int i=1;i<=cnt;i++)cout<<ru[i]<<' '<<endl; //for(int i=1;i<=cnt;i++)cout<<sz[i]<<' '<<endl; //bfs(); //for(int i=1;i<=cnt;i++)if(dis[i]>10)cout<<dis[i]<<endl; //for(int i=1;i<=cnt;i++)if(dis[i]==cnt-1)put(sz[i]),flag=0; //if(flag)put(0); //cout<<flag<<endl; for(int i=1;i<=cnt;i++)if(ru[i]==0)flag++,p=i; //cout<<flag<<endl; if(flag==1)put(sz[p]); else put(0); return 0; }
休闲的翻了一波题解发现拓扑是能写的。有bitset这个东西啊,很好价值不会再被重复累加因为有一种操作叫做按位或!!!
于是可以愉快的用拓扑排序A了这道题了,关键是没想到一种操作按位或这点需要注意。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cctype> #include<utility> #include<queue> #include<stack> #include<deque> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<ctime> #include<set> #include<bitset> #include<map> #include<cmath> #include<vector> #include<cstdlib> #define INF 2147483646 #define INF1 168430090 #define ll long long using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50002,maxn=10002; int n,m; int lin[MAXN],ver[MAXN],nex[MAXN],len=0; int clin[MAXN],cver[MAXN],cnex[MAXN],clen=0; int dfn[maxn],vis[maxn],low[maxn],num=0; int c[maxn],s[maxn],cnt,ans,t,p; int sz[maxn],q[maxn],ru[maxn],h; bitset<maxn>a[maxn]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void cadd(int x,int y) { cver[++clen]=y; cnex[clen]=clin[x]; clin[x]=clen; } void tarjan(int x) { dfn[x]=low[x]=++num; vis[x]=1;s[++t]=x; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(dfn[tn]==0) { tarjan(tn); low[x]=min(low[x],low[tn]); } else if(vis[tn]==1)low[x]=min(low[x],dfn[tn]); } if(dfn[x]==low[x]) { int y; cnt++; do { y=s[t--];vis[y]=0; c[y]=cnt;sz[cnt]++; } while(y!=x); } } void bfs() { h=t=0; for(int i=1;i<=cnt;i++)if(ru[i]==0)q[++t]=i; for(int i=1;i<=cnt;i++)a[i][i]=1; //cout<<t<<endl; while(h++<t) { int te=q[h]; for(int i=clin[te];i;i=cnex[i]) { int tn=cver[i]; ru[tn]--; a[tn]|=a[te]; if(ru[tn]==0)q[++t]=tn; } } return; } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(int i=1;i<=m;i++) { int x,y; x=read();y=read(); add(x,y); } for(int i=1;i<=n;i++)if(dfn[i]==0)tarjan(i); //for(int i=1;i<=cnt;i++)cout<<sz[i]<<endl; //put(cnt); for(int i=1;i<=n;i++) { for(int j=lin[i];j;j=nex[j]) { int tn=ver[j]; if(c[i]==c[tn])continue; cadd(c[i],c[tn]); ru[c[tn]]++; } } //for(int i=1;i<=cnt;i++)cout<<ru[i]<<' '<<endl; //for(int i=1;i<=cnt;i++)cout<<sz[i]<<' '<<endl; bfs(); for(int i=1;i<=cnt;i++)if(a[i].count()==cnt)ans+=sz[i]; put(ans); return 0; }
当然get到另一种求强联通分量的做法 叫做kosaraju 比较神奇的东西和tarjan的复杂度一样。
Kosaraju
Kosaraju 采用两次 DFS 及一次对逆图的操作从而求解的
首先 DFS 遍历所有节点,当到头后,将节点入栈,返回 DFS 遍历完后在逆图(所有边反向)里按照栈的顺序进行 DFS ,将所有能访问到的点删除,加入到当前连通分量里 直到所有点都被删除
由于强连通是环,无论图的边如何反向,应该都是能够互相访问的,而不在环里的点是无法访问到的. 要考虑的额外情况就是逆图里是否会有一个点能访问到和它不是强连通的点 假设存在这种情况,那么有以下条件: 这两个点单向连通(不连通逆图无法访问) 单向连通的子节点后入栈(这样能在父节点被删除前访问到父节点)
如果两个节点单向连通,有两种情况: 先访问到父节点 父节点能遍历到子节点,父节点会后入栈 先访问子节点 子节点在第一次遍历时,无法遍历到父节点,子节点先入栈,同上
因此,该算法可以实现强连通分量缩点的功能
步骤如下: DFS 遍历所有节点,当到达终点后入栈 在逆图里按照栈的顺序 DFS 所有节点,将所有能够访问到的点连为一个强连通分量并从图里删除 重复 2 直到所有点被删除
这个算法很有意思现在我大致是理解了,以后还需多加复习!真的比较有意思呢,个人感觉比tarjan要简单一点。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cctype> #include<utility> #include<queue> #include<stack> #include<deque> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<ctime> #include<set> #include<bitset> #include<map> #include<cmath> #include<vector> #include<cstdlib> #define INF 2147483646 #define INF1 168430090 #define ll long long using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50002,maxn=10002; int n,m; int lin[MAXN],ver[MAXN],nex[MAXN],len=0; int clin[MAXN],cver[MAXN],cnex[MAXN],clen=0; int vis[MAXN],s[maxn],top,cnt,c[maxn]; int out[maxn],sz[maxn],flag,p; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void cadd(int x,int y) { cver[++clen]=y; cnex[clen]=clin[x]; clin[x]=clen; } void dfs1(int x) { vis[x]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn])continue; dfs1(tn); } s[++top]=x; } void dfs2(int x) { vis[x]=1;c[x]=cnt;sz[cnt]++; for(int i=clin[x];i;i=cnex[i]) { int tn=cver[i]; if(vis[tn])continue; dfs2(tn); } } int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(int i=1;i<=m;i++) { int x,y; x=read();y=read(); add(x,y);cadd(y,x); } for(int i=1;i<=n;i++)if(vis[i]==0)dfs1(i); memset(vis,0,sizeof(vis)); //put(top); for(int i=top;i>=1;i--) { if(vis[s[i]])continue; cnt++; dfs2(s[i]); } for(int i=1;i<=n;i++) for(int j=lin[i];j;j=nex[j]) { int tn=ver[j]; if(c[i]==c[tn])continue; out[c[i]]++; } //for(int i=1;i<=cnt;i++)put(sz[i]); //for(int i=1;i<=cnt;i++)put(out[i]); for(int i=1;i<=cnt;i++) if(out[i]==0) { if(p)flag=1; else p=i; } if(flag==1)put(0); else put(sz[p]); return 0; }

为了联系到上述算法,特意找到了这道题玩了一波缩点 让我郁闷的是 f数组没赋初值导致没有1A比较难受
更难受的地方是利用上述算法需要建三次图,这真的让我有点吃不消。。。
至于答案的累加 直接拓扑排序找答案即可 或者记忆化搜索也行.

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cctype> #include<utility> #include<queue> #include<stack> #include<deque> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<ctime> #include<set> #include<bitset> #include<map> #include<cmath> #include<vector> #include<cstdlib> #define INF 2147483646 #define INF1 168430090 #define ll long long using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } void put(int x) { x<0?putchar('-'),x=-x:0; int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=50002,maxn=10002; int n,m; int lin[MAXN],ver[MAXN],nex[MAXN],len=0; int clin[MAXN],cver[MAXN],cnex[MAXN],clen=0; int vis[MAXN],s[maxn],top,cnt,c[maxn]; int out[maxn],sz[maxn],flag,p; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void cadd(int x,int y) { cver[++clen]=y; cnex[clen]=clin[x]; clin[x]=clen; } void dfs1(int x) { vis[x]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn])continue; dfs1(tn); } s[++top]=x; } void dfs2(int x) { vis[x]=1;c[x]=cnt;sz[cnt]++; for(int i=clin[x];i;i=cnex[i]) { int tn=cver[i]; if(vis[tn])continue; dfs2(tn); } } int main() { freopen("1.in","r",stdin); //freopen("1.out","w",stdout); n=read();m=read(); for(int i=1;i<=m;i++) { int x,y; x=read();y=read(); add(x,y);cadd(y,x); } for(int i=1;i<=n;i++)if(vis[i]==0)dfs1(i); memset(vis,0,sizeof(vis)); //put(top); for(int i=top;i>=1;i--) { if(vis[s[i]])continue; cnt++; dfs2(s[i]); } for(int i=1;i<=n;i++) for(int j=lin[i];j;j=nex[j]) { int tn=ver[j]; if(c[i]==c[tn])continue; out[c[i]]++; } cout<<cnt<<endl; //for(int i=1;i<=cnt;i++)put(sz[i]); //for(int i=1;i<=cnt;i++)put(out[i]); for(int i=1;i<=cnt;i++) if(out[i]==0) { if(p)flag=1; else p=i; } //if(flag==1)put(0); //else put(sz[p]); return 0; }
春未老,风细柳斜斜。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号