线段树
早就要学主席树了,可是发现自己连线段树都不会了。
然后重学线段树 搞了几波例题,感觉还不错,不管是状态(自己的)还是细节,还是思路都是有的。

这道题呢 一道算是对5个月前的我来说比较鬼畜的题了。
但是对现在的我的话却是如此简单,尽管浏览了一遍以前的代码。*(我还是会的
考虑lazy tag 先加后乘 这样 就没什么问题了 至于一些细节在我看来就自然了很多呢。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define l(x) t[x].l #define r(x) t[x].r #define s(x) t[x].sum #define p(x) t[x].add1 #define m(x) t[x].add using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline long long read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(long long x) { x<0?putchar('-'),x=-x:0; long long num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const long long MAXN=100002; struct wy { long long l,r; long long sum; long long add;//乘法 long long add1;//加法 }t[MAXN<<2]; long long n,m,mod; long long a[MAXN]; void build(long long p,long long l,long long r) { l(p)=l;r(p)=r;m(p)=1;p(p)=0; if(l==r){s(p)=a[l]%mod;return;} long long mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); s(p)=(s(p<<1)+s(p<<1|1))%mod; } void pushdown(long long p) { m(p<<1)=(m(p<<1)*m(p))%mod; m(p<<1|1)=(m(p<<1|1)*m(p))%mod; p(p<<1)=(p(p<<1)*m(p))%mod; p(p<<1|1)=(p(p<<1|1)*m(p))%mod; p(p<<1)=(p(p<<1)+p(p))%mod; p(p<<1|1)=(p(p<<1|1)+p(p))%mod; s(p<<1)=(s(p<<1)*m(p))%mod; s(p<<1|1)=(s(p<<1|1)*m(p))%mod; s(p<<1)=(s(p<<1)+p(p)*(r(p<<1)-l(p<<1)+1))%mod; s(p<<1|1)=(s(p<<1|1)+p(p)*(r(p<<1|1)-l(p<<1|1)+1))%mod; m(p)=1;p(p)=0;return; } void change(long long p,long long l,long long r,long long d) { if(l<=l(p)&&r>=r(p)) { s(p)=(s(p)*d)%mod; m(p)=(m(p)*d)%mod; p(p)=(p(p)*d)%mod; return; } pushdown(p); long long mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,r,d); if(r>mid)change(p<<1|1,l,r,d); s(p)=(s(p<<1)+s(p<<1|1))%mod; } void change1(long long p,long long l,long long r,long long d) { if(l<=l(p)&&r>=r(p)) { s(p)=(s(p)+d*(r(p)-l(p)+1))%mod; p(p)=(p(p)+d)%mod; return; } pushdown(p); long long mid=(l(p)+r(p))>>1; if(l<=mid)change1(p<<1,l,r,d); if(r>mid)change1(p<<1|1,l,r,d); s(p)=(s(p<<1)+s(p<<1|1))%mod; } long long ask(long long p,long long l,long long r) { if(l<=l(p)&&r>=r(p))return s(p); pushdown(p); long long mid=(l(p)+r(p))>>1; long long cnt=0; if(l<=mid)cnt=(cnt+ask(p<<1,l,r))%mod; if(r>mid)cnt=(cnt+ask(p<<1|1,l,r))%mod; return cnt%mod; } int main() { //freopen("1.in","r",stdin); n=read();m=read();mod=read(); for(long long i=1;i<=n;i++)a[i]=read(); build(1,1,n); for(long long i=1;i<=m;i++) { long long p,x,y,k; p=read(); if(p==1) { x=read();y=read();k=read(); change(1,x,y,k); } if(p==2) { x=read();y=read();k=read(); change1(1,x,y,k); } if(p==3) { x=read();y=read(); put(ask(1,x,y)); } } return 0; }
值得一提的是我曾经有一个在康神看来比较蠢的做法,就是不下传懒标记,只在ask的时候下传。
仔细思考也是可以的(当然是在一定的条件下。
仔细分析 我想 是 只有在单点询问的时候 才可以只要做,因为曾经有个学长 曾经秒回过我。
当然是lzx学长了:

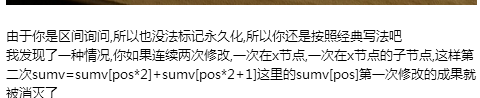
理由如上我想只有sum不是区间的值的话才有我的小猜想的正确性。(能跑的快一丢丢。

对于这道题我想 我不会啊 然后有一个直接的想法就是差分线段树。
不太会差分 很简单的东西随便写了一下 90 比较可惜没有1 A
然后呢 我决定 看题解了,发现一些小细节打挂了(主要是本题坑点太多)
考虑差分线段树每次修改时维护一下树中区间的和然后单点查询就可以直接求前缀和即可。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define l(x) t[x].l #define r(x) t[x].r #define sum(x) t[x].sum #define c(x) t[x].add using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline long long read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(long long x) { x<0?putchar('-'),x=-x:0; long long num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const long long MAXN=200002; long long a[MAXN]; long long n,m; struct wy//差分线段树 { long long l,r; long long sum;//区间和 long long add;//lazy tag 差分数 }t[MAXN<<2]; void pushdown(long long p) { if(c(p)==0)return; sum(p<<1)+=(r(p<<1)-l(p<<1)+1)*c(p); sum(p<<1|1)+=(r(p<<1|1)-l(p<<1|1)+1)*c(p); c(p<<1)+=c(p);c(p<<1|1)+=c(p); c(p)=0; return; } void build(long long p,long long l,long long r) { l(p)=l;r(p)=r;sum(p)=0; if(l==r)return; long long mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); } void change(long long p,long long l,long long r,long long d) { if(l<=l(p)&&r>=r(p)) { sum(p)+=(r(p)-l(p)+1)*d; c(p)+=d; return; } pushdown(p); long long mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,r,d); if(r>mid)change(p<<1|1,l,r,d); sum(p)=sum(p<<1)+sum(p<<1|1); } long long ask(long long p,long long l,long long r) { if(l<=l(p)&&r>=r(p))return sum(p); pushdown(p); long long cnt=0; long long mid=(l(p)+r(p))>>1; if(l<=mid)cnt+=ask(p<<1,l,r); if(r>mid)cnt+=ask(p<<1|1,l,r); return cnt; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(long long i=1;i<=n;i++)a[i]=read(); build(1,1,n); for(long long i=1;i<=m;i++) { long long p,l,r,k,d; p=read(); if(p==1) { l=read();r=read(); k=read();d=read(); change(1,l,l,k); if(l!=r)change(1,l+1,r,d); long long cnt=k+(r-l)*d; if(r+1<=n)change(1,r+1,r+1,-cnt); } if(p==2) { l=read(); //cout<<l<<endl; put(ask(1,1,l)+a[l]); } } //for(long long i=1;i<=n;i++)cout<<ask(1,1,i)+a[i]<<' '; return 0; }

对于这道题我也想出了 正解尽管很简单 考虑每次插入。
其实就是 单点修改罢了 先建一颗线段树。然后每次询问的时候 单点修改即可。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define l(x) t[x].l #define r(x) t[x].r #define m(x) t[x].maxx #define ll long long using namespace std; /*char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; }*/ inline long long read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(long long x) { x<0?putchar('-'),x=-x:0; long long num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar('\n');return; } const int MAXN=200002; int n,mod,h=0,last; char a; struct wy { int l,r; int maxx; }t[MAXN<<2]; void build(int p,int l,int r) { l(p)=l;r(p)=r;m(p)=0; if(l==r)return; int mid=(l+r)>>1; build(p<<1,l,mid); build(p<<1|1,mid+1,r); } void change(int p,int l,int r,int d) { if(l<=l(p)&&r>=r(p)) { m(p)=d; return; } int mid=(l(p)+r(p))>>1; if(l<=mid)change(p<<1,l,r,d); if(r>mid)change(p<<1|1,l,r,d); m(p)=max(m(p<<1),m(p<<1|1))%mod; } int ask(int p,int l,int r) { if(l<=l(p)&&r>=r(p))return m(p); int mid=(l(p)+r(p))>>1; int cnt=-INF;//需注意 if(l<=mid)cnt=max(ask(p<<1,l,r),cnt); if(r>mid)cnt=max(cnt,ask(p<<1|1,l,r)); return cnt; } int main() { //freopen("1.in","r",stdin); n=read();mod=read(); build(1,1,200000); for(int i=1;i<=n;i++) { cin>>a; int x; x=read(); if(a=='A') { int cnt=((ll)(last+x)%mod);h++; change(1,h,h,cnt); } if(a=='Q') { last=ask(1,h-x+1,h); put(last); } } }
江南好风,景落花时节又逢。夜来风雨,春归似欲留人。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号