再探树形dp
随着校oj终于刷进了第一页,可以不用去写那些水题了,开始认真学习自己的东西,当然包括文化课。努力。。
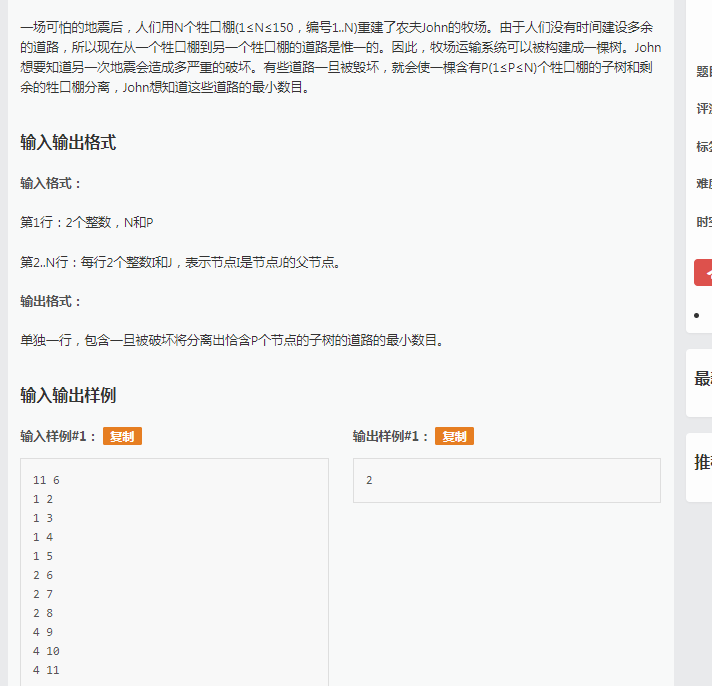
这道题呢是道树形dp,可看到了根本就不知道怎么写思考过程:
5min 终于看懂了题 画了样例的图把输出看懂了 然后发现这不可做。。
设个状态吧,这肯定是从子树上进行转移的然后然后f[i]表示以i为根节点子树的大小吧。然后真的就不可做了。
想列状态转移方程发现价值算不出来放弃,脑抽没有多加一维状态来表示价值哎。
无奈点开题解 1min恍然大悟。。dp好难。
其实这道题就是一个简单的树形背包dp,细节处理的不多。可是真的不好想。

#include<iostream> #include<cstring> #include<string> #include<ctime> #include<cmath> #include<iomanip> #include<algorithm> #include<queue> #include<vector> #include<stack> #include<cstdio> #include<map> #include<deque> #include<set> #define inf 1000000000 using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=200; int n,m,ru[maxn]; int lin[maxn<<1],ver[maxn<<1],nex[maxn<<1],len=0; int vis[maxn],ans=inf,f[maxn][maxn];//f[i][j]表示第i个节点保留j条边需要截下的最小代价 void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dfs(int x) { vis[x]=1; f[x][1]=ru[x];//只保留x节点的话需要砍ru[x]条边 for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn]==1)continue; dfs(tn); for(int j=m;j>=1;j--)//01背包模型 for(int k=1;k<j;k++) f[x][j]=min(f[x][j],f[x][k]+f[tn][j-k]-2); //-2原因为现在加上儿子节点的这么多边后可以少砍f[x][k]少砍1条,f[tn][j-k]少砍一条 } } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<n;i++) { int x,y; x=read();y=read(); add(x,y);add(y,x); ru[x]++;ru[y]++; } memset(f,10,sizeof(f)); dfs(1); for(int i=1;i<=n;i++)ans=min(ans,f[i][m]); printf("%d\n",ans); return 0; }
一中午时间学习了一下树形dp的二次扫描+换根,觉得不算是很难,dp转移方程也很好推就是有点绕。
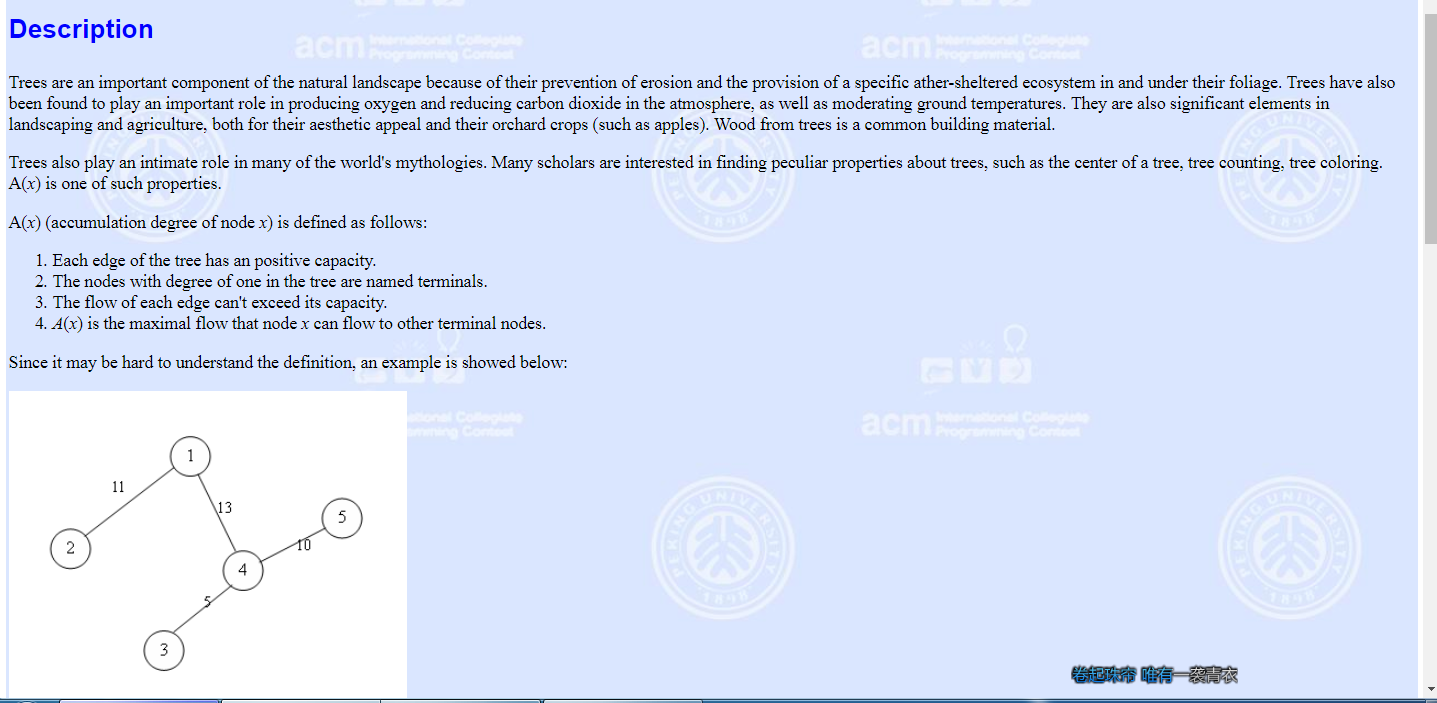
主要是一个求出最大的源点能发出的水量 poj3585
n的范围20000 直接O(n^2)爆力直接超时,考虑O(n)求出。设d[i]表示以i为节点从i的子树身上所能的到的最大水量。
则有d[x]+=((ru[tn]==1)?e[i]:min(d[tn],e[i]));直接在O(n)时间之内求出d数组,这也就是这道题的难点了,我们不知道跟在哪,所以外面加上一层for循环的话直接就是O(n)的了,考虑怎么搞出来全部点。设f[i]表示以i为根节点所能得到的最大值,随便设root=1;先假设root为根,把d数组跑出来。
之后求f数组就行了,显然f[root]=d[root];然后通过这一点进行对f数组进行更新。
看完书后得到f[tn]=d[tn]+((ru[x]==1)?e[i]:min(f[x]-min(d[tn],e[i]),e[i]));看图理解的快很神奇就实现了换根!
于是有代码:

#include<iostream> #include<cstring> #include<string> #include<ctime> #include<cmath> #include<iomanip> #include<algorithm> #include<queue> #include<vector> #include<stack> #include<cstdio> #include<map> #include<deque> #include<set> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=200002; int t,n; int ver[maxn<<1],lin[maxn<<1],nex[maxn<<1],e[maxn<<1],len=0; int vis[maxn],d[maxn],ru[maxn],f[maxn],root,ans=0; void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } void dp(int x) { vis[x]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn]==1)continue; dp(tn); if(ru[tn]==1)d[x]+=e[i]; else d[x]+=min(d[tn],e[i]); } } void dfs(int x) { vis[x]=1; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn]==1)continue; if(ru[x]==1)f[tn]=d[tn]+e[i]; else f[tn]=d[tn]+min(f[x]-min(d[tn],e[i]),e[i]); dfs(tn); } } int main() { //freopen("1.in","r",stdin); t=read(); while(t--) { memset(lin,0,sizeof(lin)); memset(e,0,sizeof(e)); memset(ru,0,sizeof(ru)); memset(d,0,sizeof(d)); memset(f,0,sizeof(f)); ans=0;root=1;len=0; n=read(); for(int i=1;i<n;i++) { int x,y,z; x=read();y=read();z=read(); add(x,y,z);add(y,x,z); ru[x]++;ru[y]++; } memset(vis,0,sizeof(vis)); dp(root); memset(vis,0,sizeof(vis)); f[root]=d[root]; dfs(root); for(int i=1;i<=n;i++)ans=max(ans,f[i]); printf("%d\n",ans); } return 0; }
成就感足足的。
然后做了一道这段时间的最后一道总结树形dp的题,依然是依赖性背包,很不好想我觉得,很难受的感觉。也就是非常难以下手的题目。

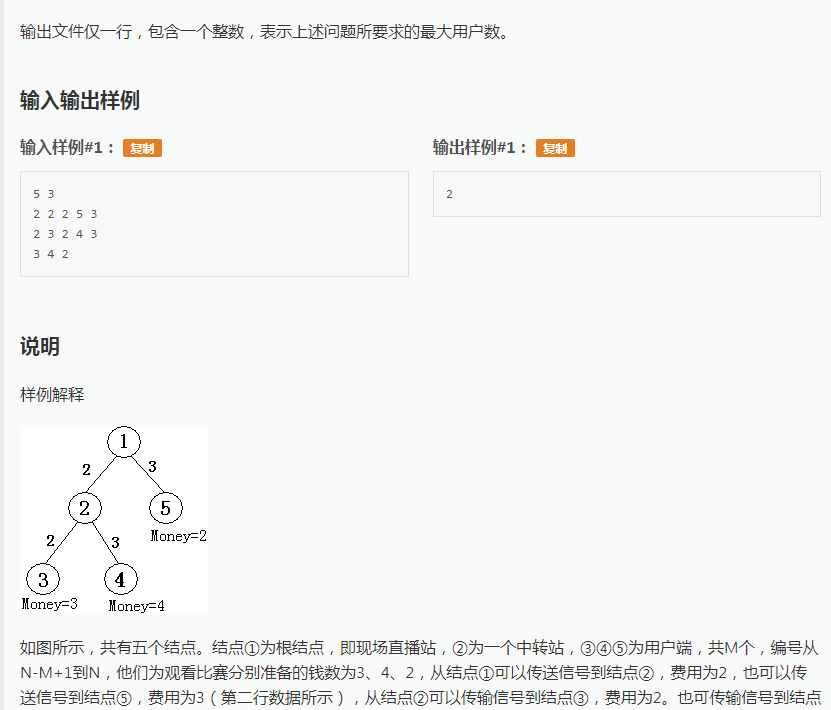
求出最多给多少个顾客发信号且费用不为负数。难以下手,知道是树形依赖背包dp,但是价值和最后的顾客数考虑怎么累加。
设状态f[i][j]表示以i为节点的这颗子树给j个终端顾客发信号可以使得赚的价钱最多。这里很明显这个状态是和题目不照的,题目是说最多能给多少个顾客发信号。
然后其实我们只要便利一遍f[1][i]使得f值为正且i最大就是本题答案,如此巧妙的转化。
然后开始写dp式子,发现怎么像上图的2节点根本不是价值咋么办,所以f初值全部设为负无穷,f[x][0]=0;每次dp时执行这个操作,顺带在输入时记录每个点的度数能求出终端客户,f[x][1]=v[x];然后套用普通的背包dp即可。然后就会tle4个点,因为你根本不知道当前点有多少个子节点所以你进行背包dp时大小不知道,这时可以先预处理出每个点的子树大小,再进行背包dp的转移就可以愉快的a掉这道题了!这些题目都是很好的题,要时常复习啊。
#include<bits/stdc++.h> #include<iostream> #include<cmath> #include<cstdio> #include<ctime> #include<cstring> #include<string> #include<queue> #include<deque> #include<vector> #include<stack> #include<map> #include<algorithm> #include<iomanip> #include<set> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void put(int x) { if(x==0){putchar('0');putchar('\n');return;} if(x<0)x=-x,putchar('-'); int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; while(num)putchar(ch[num--]); putchar('\n');return; } const int maxn=3002; int n,m,ans=0; int lin[maxn<<1],ver[maxn<<1],nex[maxn<<1],e[maxn<<1],len=0; int v[maxn],sz[maxn],f[maxn][maxn];//f[i][j]表示以i为子树选取j个子节点所能得到的价值最大 void add(int x,int y,int z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } void dfs1(int x) { for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; dfs1(tn); sz[x]+=sz[tn]; } sz[x]++; } void dfs(int x) { f[x][0]=0;if(sz[x]==1)f[x][1]=v[x]; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; dfs(tn); for(int j=sz[x];j>=0;j--) for(int k=0;k<=j;k++) f[x][j]=max(f[x][j],f[x][j-k]+f[tn][k]-e[i]); } } int main() { //freopen("1.in","r",stdin); n=read();m=read(); memset(f,0xcf,sizeof(f)); for(int i=1;i<=n-m;i++) { int x;x=read(); for(int j=1;j<=x;j++) { int y,z;y=read();z=read(); add(i,y,z); } } dfs1(1); for(int i=1;i<=m;i++)v[n-m+i]=read(); dfs(1); for(int i=m;i>=0;i--)if(f[1][i]>=0){put(i);return 0;} //for(int i=1;i<=n;i++)put(sz[i]); return 0; }
且放白鹿青崖间。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号