归并排序

算法思想

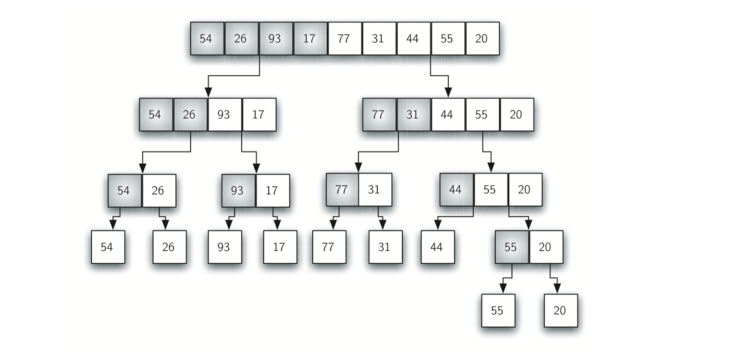
1. 分解 :将当前区间一分为二；
2. 求解: 递归地对两个子区间进行归并排序，递归的终结条件是子区间长度为1。
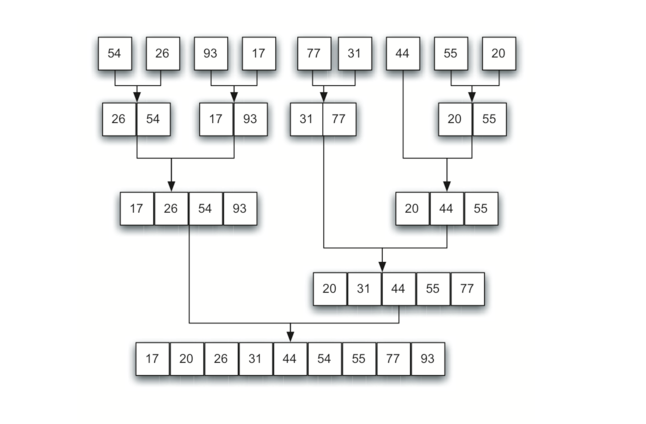
3. 合并：将已排序的两个子区间归并为一个有序的区间。

分裂：

合并：

动画演示：

实现

C++

void mergeSortHelp(vector<int> &a, int tmp[], int left, int right)
{
	if (left == right)
		return;
	int mid = (left + right) / 2;
	mergeSortHelp(a, tmp, left, mid);
	mergeSortHelp(a, tmp, mid + 1, right);
	for (int i = left; i <= right; i++)
		tmp[i] = a[i];
	int i = left;
	int j = mid + 1;
	int k = left;
	while (k <= right)
	{
		if (j > right)
			a[k++] = tmp[i++];
		else if (i > mid)
			a[k++] = tmp[j++];
		else if (tmp[i] < tmp[j])
			a[k++] = tmp[i++];
		else a[k++] = tmp[j++];
	}
}

void mergeSort(vector<int> &a)
{
	int len = a.size();
	int *tmp = new int[len];
	mergeSortHelp(a, tmp, 0, len - 1);
	delete[]tmp;
}

python

def mergeSort(alist):
    #列表元素个数小于等于1是基本情况
    if len(alist)>1:
        mid = len(alist) // 2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        #递归调用归并排序
        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0

        #左右两边比较取小者添加到列表中
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i < len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1

总结

稳定性：
因为我们在遇到相等的数据的时候必然是按顺序“抄写”到辅助数组上的，所以，归并排序同样是稳定算法。

适用场景：
归并排序在数据量比较大的时候也有较为出色的表现（效率上），但是，其空间复杂度O(n)使得在数据量特别大的时候（例如，1千万数据）几乎不可接受。考虑到有的机器内存本身就比较小，因此，采用归并排序一定要注意。

复杂度：
\(O(N * \log N)\) 。